四川省成都市武侯区2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 2021年3月1日起，成都市全面推行生活垃圾分类.下列垃圾分类的图标中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 把一个不等式的解集表示在数轴上，如图所示，则该不等式的解集为（）

A、x＜1 B、x≥1 C、x＞1 D、x≤1

查看试题解析
3. 要使▱ABCD成为矩形，需要添加的条件是（）

A、AB＝BC B、AC⊥BD C、∠ABC＝90° D、∠ABD＝∠CBD

查看试题解析
4. 下列分式变形正确的是（）

A、 $\frac{a^{2}}{b^{2}} = \frac{a}{b}$ B、 $\frac{2 a}{2 b} = \frac{a}{b}$ C、 $\frac{2 a + 1}{4 b} = \frac{a + 1}{2 b}$ D、 $\frac{a + 2}{b + 2} = \frac{a}{b}$

查看试题解析
5. 把多项式a³b⁴﹣abⁿc因式分解时，提取的公因式是ab⁴ ，则n的值可能为（）

A、5 B、3 C、2 D、1

查看试题解析
6. 若a，b，c分别是 $△$ ABC的三边长，且满足a²﹣2ab+b²＝0，b²﹣c²＝0，则 $△$ ABC的形状是（）

A、直角三角形 B、钝角三角形 C、等腰直角三角形 D、等边三角形

查看试题解析
7. 如图，点A，B的坐标分别为（﹣2，1），（0，﹣2）.若将线段AB平移至A₁B₁ ，且点A₁ ， B₁的坐标分别为（1，4），（a，1），则a的值为（）

A、0 B、1 C、2 D、3

查看试题解析
8. 如图，在矩形ABCD中，∠ADC的平分线交BC于点E，将一块三角板的直角顶点放在点E处，一条直角边经过点A，另一条直角边交CD于点M，若DM＝2CM＝4，则BC的长为（）

A、8 B、7 C、5 D、4

查看试题解析
9. 下列各命题中是假命题的是（）

A、如果ab＝0，那么a＝0或b＝0 B、如果点P的坐标为（﹣2，a²+1），则点P在第二象限 C、三角形的中位线等于此三角形一边的一半 D、在一个角的内部，到角的两边距离相等的点在这个角的平分线上

查看试题解析
10. 已知y与x之间满足的函数关系如图所示，其中，当x≥0时，y＝x；当x＜0时，y＝﹣2x+1，则当函数值y＞3时，x的取值范围为（）

A、x＜﹣1 B、x＞3 C、﹣1＜x＜3 D、x＜﹣1或x＞3

查看试题解析

二、填空题

11. 已知x+y＝2，则 $\frac{1}{2}$ （x²+2xy+y²）的值为.

查看试题解析
12. 若 $\frac{m}{n}$ ＝2，则分式 $\frac{m - n}{m + 2 n}$ 的值为.

查看试题解析
13. 如图，在 $△$ ABC中，CA＝CB，∠ACB＝100°，点D在边AB上，以点D为圆心，适当长为半径作弧，交AB于点E，F.再分别以点E，F为圆心，以大于 $\frac{1}{2}$ EF的长为半轻作弧，两弧相交于点G，作射线DG交AC的延长线于点H，则∠CHD的度数为.

查看试题解析
14. 如图，在平行四边形ABCD中，AB＝4，沿对角线AC翻折，点B的对应点为 $B^{'}$ ， $B^{'} C$ 与AD交于点E，此时 $△$ CDE恰为等边三角形，则重叠部分（即图中阴影部分）的面积为.

查看试题解析
15. 若关于x的多项式x²﹣（k﹣2021）x+9是完全平方式，则k的值为.

查看试题解析
16. 若关于x的一元一次不等式组 ${\begin{array}{l} x \geq b - 1 \\ x < \frac{a}{2} \end{array}$ 的解集为﹣3≤x＜ $\frac{3}{2}$ ，则b^a＝.

查看试题解析
17. 如图，在 $△$ ABC中，AD平分∠BAC，BD⊥AD于点D，延长BD交AC于点E，点F为BC中点，连接DF.若AB＝6，AC＝10， $△$ ABC的面积为30，则 $△$ BDF的面积为.

查看试题解析
18. 如图，在正方形ABCD中，AB＝4cm，点E是AD的中点，动点F从点A出发，以2cm/s的速度沿AB向终点B运动，设点F的运动时间为ts，当 $△$ CEF为等腰三角形时，t的值是.

查看试题解析
19. 如图，点D，E是 $△$ ABC内的两点，且DE $/ /$ AB，连结AD，BE，CE.若AB＝9 $\sqrt{2}$ ，DE＝2 $\sqrt{2}$ ，BC＝10，∠ABC＝75°，则AD+BE+CE的最小值为.

查看试题解析

三、解答题

20.

(1)、因式分解：（x+1）（x﹣3）+4.

(2)、解不等式组 ${\begin{array}{l} \frac{1}{2} (x - 2) \leq 1 \\ \frac{x + 1}{2} > \frac{x + 2}{3} \end{array}$ ，并将其解集表示在所给数轴上.

查看试题解析
21. 先化简： $(1 - \frac{1}{x + 2}) \div \frac{x^{2} - 1}{x + 2}$ ，然后从﹣2，﹣1，1， $\sqrt{2}$ +1四个数中选一个合适的数代入化简后的结果中进行求值.

查看试题解析
22. 如图，在菱形ABCD中，AC与BD相交于点E，若BD＝ $4 \sqrt{5}$ ，菱形ABCD的周长为20，求菱形ABCD的面积.

查看试题解析
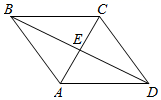23. 铁路是经济发展的大动脉，作为成渝地区双层经济圈建设的标志性工程“成渝中线高铁”力争年内开工建设，其设计行驶速度为400km/h，按此设计行驶速度，行驶300km所花时间将比普通列车行驶300km所花时间少 $\frac{7}{4}$ h，求普通列车的行驶速度.

查看试题解析
24. 如图，方格纸中每个小正方形的边长都是1个单位长度，建立平面直角坐标系xOy，已知A（3，1），B（2，﹣2），连接AB.

(1)、在图中画出线段AB绕点A按顺时针方向旋转90°后的线段AC，并直接写出点C的坐标；

(2)、在（1）的基础上，连接BC，求 $△$ ABC的面积；

(3)、在（2）的基础上，在y轴上取一点P，连接PB，PC.当 $△$ BCP的面积与 $△$ ABC的面积相等时，求点P的坐标.

查看试题解析
25. 已知点E是正方形ABCD的边CD上的动点，连接AE，过点A作AF⊥AE，交CB的延长线于点F.

(1)、如图1，求证：FB＝ED；

(2)、点G为正方形ABCD的对角线BD上一点，连接AG，GC，GF，且GC＝GF.
①如图2，求∠GFA的度数；

②如图3，过点G作MH $/ /$ AE，分别交AF，AB，DC于点M，N，H.若AB＝3，BF＝1，求MH的长.

查看试题解析
26. 阅读材料：对于非零实数m，n，若关于x的分式 $\frac{(x - m) (x - n)}{x}$ 的值为零，则x＝m或x＝n.又因为 $\frac{(x - m) (x - n)}{x}$ ＝ $\frac{x^{2} - (m + n) x + m n}{x}$ ＝x+ $\frac{m m}{x}$ ﹣（m+n），所以关于x的方程x+ $\frac{m n}{x}$ ＝m+n的解为x₁＝m，x₂＝n.

(1)、理解应用：方程x+ $\frac{1}{x}$ ＝2+ $\frac{1}{2}$ 的解为：x₁＝， x₂＝；

(2)、拓展提升：若关于x的方程x+ $\frac{4}{x}$ ＝k﹣1的解满足x₁＝x₂ ，求k的值.

查看试题解析
27. 已知在 $△$ ABC中，∠ECF的两边与 $△$ ABC的边AB从左至右依次交于点E，F，且∠ECF＝ $\frac{1}{2}$ ∠ACB.

(1)、如图1，若AC＝BC，∠ACB＝90°，将△ACE绕点C逆时针旋转90°后，得到 $△$ BCG，连接FG.求证： $△$ ECF≌ $△$ GCF；

(2)、如图2，若AC＝BC，∠ACB＝120°，BF＝3，AE＝2，求线段EF的长；

(3)、如图3，若∠ACB＝90°，AC＝2 $\sqrt{5}$ ，BC＝ $\sqrt{5}$ ，设AE＝y，BF＝x（0＜x＜1），请用含x的代数式表示y（直接写出结果，不必写解答过程）.

查看试题解析
28. 如图1，在平面直角坐标系xOy中，直线l₁：y＝x+6交x轴于点A，交y轴于点B，经过点B的直线l₂：y＝kx+b交x轴于点C，且l₂与l₁关于y轴对称.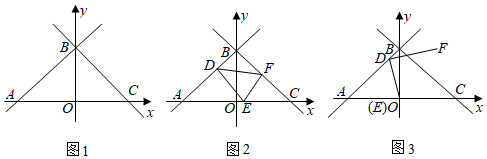

(1)、求直线l₂的函数表达式；

(2)、点D，E分别是线段AB，AC上的点，将线段DE绕点D逆时针α度后得到线段DF.
①如图2，当点D的坐标为（﹣2，m），α＝45°，且点F恰好落在线段BC上时，求线段AE的长；

②如图3，当点D的坐标为（﹣1，n），α＝90°，且点E恰好和原点O重合时，在直线y＝3﹣ $\sqrt{13}$ 上是否存在一点G，使得∠DGF＝∠DGO？若存在，直接写出点G的坐标；若不存在，请说明理由.

查看试题解析