广西壮族自治区梧州市岑溪市2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 化简 $\sqrt{{(- 3)}^{2}}$ 的结果是（）

A、 $3$ B、 $- 3$ C、 $\pm 3$ D、 $9$

查看试题解析
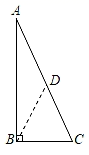
2. 五边形的内角和是（）

A、180° B、360° C、540° D、720°

查看试题解析
3. 下列二次根式中，能与 $\sqrt{3}$ 合并的是（）

A、 $\sqrt{30}$ B、 $\sqrt{24}$ C、 $\sqrt{18}$ D、 $\sqrt{12}$

查看试题解析
4. 某小区有一个直角三角形小花园ABC（如图），其中∠ABC＝90°，AB＝12m，BC＝5m，为了方便和美观，准备在小花园中间修一条小路，从顶点B修到AC边的中点D，则所修小路BD的最短距离为（）

A、6m B、6.5m C、7m D、8.5m

查看试题解析
5. 关于 $x$ 的一元二次方程 $a x^{2} - 2 x + 2 = 0$ 有两个相等的实数根，则 $a$ 的值为（）

A、 $\frac{1}{2}$ B、 $- \frac{1}{2}$ C、 $1$ D、- $1$

查看试题解析
6. 一元二次方程x²＝3x的根是（）

A、3 B、3或﹣3 C、0或3 D、 $\sqrt{3}$ 或 $- \sqrt{3}$

查看试题解析
7. 有一个矩形，它的相邻两边长分别为1和2，则它的对角线长为（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、3 D、2 $\sqrt{2}$

查看试题解析
8. 一组数据：4，7，3，8，5，7的众数和中位数分别是（）

A、7，6 B、7，5.5 C、6，6 D、6，6.5

查看试题解析
9. 下列计算正确的是（）

A、 $\sqrt{5} - \sqrt{3}$ ＝ $\sqrt{2}$ B、 $3 \sqrt{\frac{1}{3}}$ ＝ $\sqrt{3}$ C、 $\sqrt{2} \cdot \sqrt{3}$ ＝ $\sqrt{5}$ D、 $\sqrt{10}$ ÷ $\sqrt{5}$ ＝2

查看试题解析
10. 用同一种正多边形地砖镶嵌地板，这种正多边形地砖不能是（）

A、等边三角形 B、正方形 C、正六边形 D、正八边形

查看试题解析
11. 下列命题是假命题的是（）

A、四个角都相等的四边形是矩形 B、四条边都相等的四边形是菱形 C、平行四边形的对角线相等 D、菱形的对角线互相垂直平分

查看试题解析
12. 如图，点E是正方形ABCD对角线BD上的一点，连接CE、AE，延长CE交AD于点F，若∠DCE＝25°，则∠AEF的度数是（）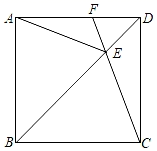

A、25° B、30° C、35° D、40°

查看试题解析

二、填空题

13. 要使式子 $\sqrt{2 x + 8}$ 有意义，则x的取值范围是.

查看试题解析
14. 若关于x的方程x²＋ax﹣2＝0有一个根是﹣1，则另一个根是.

查看试题解析
15. 下表是小健家去年每月用水量的频数统计表，则小健家去年平均每月的用水量是m³

月用水量（m³）

⁸

⁹

10

11

12

频数（月数）

³

⁴

²

²

1

查看试题解析
16. 如图，菱形ABCD的周长为24，对角线AC，BD交于点O，点E是BC的中点，则OE的长是.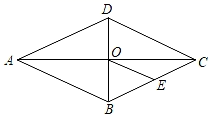

查看试题解析
17. 数据：1，2，3，2的方差是.

查看试题解析
18. 如图，把矩形纸片ABCD沿直线AE折叠，使点D落在BC边上的点F处，已知AB＝6，BC＝10，则线段CE的长为.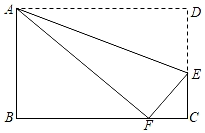

查看试题解析

三、解答题

19. 计算： $\sqrt{27}$ ﹣ $\sqrt{2} \times \sqrt{6}$ .

查看试题解析
20. 解方程：x²﹣5x+6＝0

查看试题解析
21. 已知，如图，点E、F分别在▱ABCD的边BC，DA上，且BE＝DF.求证：AE＝CF.

查看试题解析

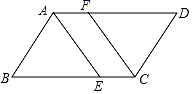22. 今年是中国共产党成立100周年.前不久，某校组织了八年级学生共同参与的“党史知识”竞赛.数学兴趣小组为了了解竞赛成绩情况，从中随机抽取了40名学生的竞赛成绩进行分析，并根据数据绘制出频数分布表和频数分布直方图：

组别	竞赛成绩x分	频数（人数）
第1组	50≤x＜60	2
第2组	60≤x＜70	8
第3组	70≤x＜80	m
第4组	80≤x＜90	16
第5组	90≤x＜100	4

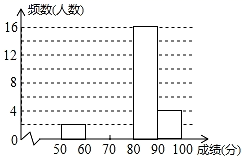
请结合图表完成下列各题：

(1)、表中m的值是.

(2)、把频数分布直方图补充完整；

(3)、按照竞赛方案，成绩在90分以上（含90分）的同学评为一等奖，若该校八年级共有学生320人，根据以上分析，估计该校八年级共有多少人获得一等奖？

查看试题解析

23. 如图，有一块四边形草坪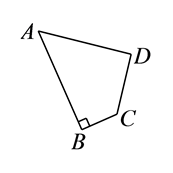， $∠ B = 90 °$ ， $A B = 24 m$ ， $B C = 7 m$ ， $C D = 15 m$ ， $A D = 20 m$ ，求：该草坪面积.

查看试题解析
24. 如图，在△ABC中，D，E，F分别是AB，BC，AC的中点，连接DF，EF，BF.

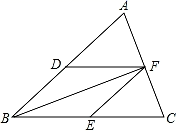(1)、求证：四边形BEFD是平行四边形；

(2)、若BF恰好是∠ABC的角平分线，则四边形BEFD是菱形吗？请说明理由.

查看试题解析
25. 如图，某城建部门计划在新修的城市广场的一块长方形空地上修建一个面积为1200m²的停车场，将停车场四周余下的空地修建成同样宽的通道，已知长方形空地的长为50m ，宽为40m ．

(1)、求通道的宽度；

(2)、某公司希望用80万元的承包金额承揽修建广场的工程，城建部门认为金额太高需要降价，通过两次协商，最终以51.2万元达成一致，若两次降价的百分率相同，求每次降价的百分率．

查看试题解析
26. 如图，在正方形ABCD中，点E是BC上的一点，点F是CD延长线上的一点，且BE＝DF，连接AE、AF、EF.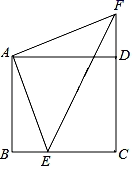

(1)、求证：△ABE≌△ADF；

(2)、若AE＝5，请求出EF的长.

查看试题解析

月用水量（m³）	⁸	⁹	10	11	12
频数（月数）	³	⁴	²	²	1