广西壮族自治区钦州市浦北县2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 下列根式中，是最简二次根式的是（）

A、 $\sqrt{\frac{1}{2}}$ B、 $\sqrt{4}$ C、 $\sqrt{5}$ D、 $\sqrt[3]{7}$

查看试题解析
2. 已知a，b，c为△ABC的三边，且满足a²+b²﹣c²＝0，则△ABC是（）

A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形

查看试题解析
3. 下列计算正确的是（）

A、 $\sqrt{3} + \sqrt{2} = \sqrt{5}$ B、 $\sqrt{3} - \sqrt{2} = 1$ C、 $\sqrt{3} \times \sqrt{2} = \sqrt{6}$ D、 $\sqrt{3} \div \sqrt{2} = 1$

查看试题解析
4.
如图，矩形ABCD的顶点A、C分别在直线a、b上，且a∥b，∠1=60°，则∠2的度数为（）

A、30° B、45° C、60° D、75°

查看试题解析
5. 一组数据3，4，4，5，若添加一个数4，则发生变化的统计量是（）

A、平均数 B、众数 C、中位数 D、方差

查看试题解析
6. 将函数y=﹣3x的图象沿y轴向上平移2个单位长度后，所得图象对应的函数关系式为（）

A、 $y = - 3 x + 2$ B、 $y = - 3 x - 2$ C、 $y = - 3 (x + 2)$ D、 $y = - 3 (x - 2)$

查看试题解析
7. 已知四边形 $A B C D$ ，对角线 $A C$ 与 $B D$ 交于点O，从下列条件中：① $A B / / C D$ ；② $A D = B C$ ；③ $∠ A B C = ∠ A D C$ ；④ $O A = O C$ .任取其中两个，以下组合能够判定四边形 $A B C D$ 是平行四边形的是（）

A、①② B、②③ C、②④ D、①④

查看试题解析
8. 如图是甲、乙两名射击运动员某节训练课的5次射击成绩的折线统计图，下列判断正确的是（）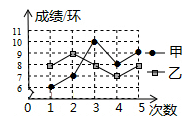

A、乙的最好成绩比甲高 B、乙的成绩的平均数比甲小 C、乙的成绩的中位数比甲小 D、乙的成绩比甲稳定

查看试题解析
9. 如图，已知菱形ABCD的对角线AC，BD的长分别为4，6，AE⊥BC于点E，则AE的长是（）

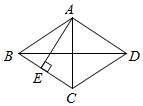A、3 B、 $\frac{12 \sqrt{13}}{13}$ C、 $\sqrt{13}$ D、 $\frac{13 \sqrt{13}}{12}$

查看试题解析
10. 对于函数y＝2x+1，下列结论错误的是（）

A、当x＞1时，y＜0 B、y随x的增大而增大 C、它的图象必经过点（0，1） D、它的图象经过第一、二、三象限

查看试题解析
11. 勾股定理是人类最伟大的科学发现之一，在我国古算书《周髀算经》中早有记载。如图1，以直角三角形的各边为边分别向外作正方形，再把较小的两张正方形纸片按图2的方式放置在最大正方形内.若知道图中阴影部分的面积，则一定能求出（）

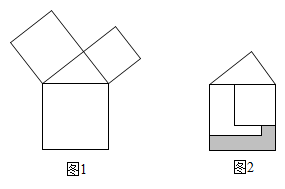A、直角三角形的面积 B、最大正方形的面积 C、较小两个正方形重叠部分的面积 D、最大正方形与直角三角形的面积和

查看试题解析
12. 如图，在△ABC中，AB＝3，AC＝4，BC＝5，P为边BC上一动点，PE⊥AB于点E，PF⊥AC于点F，则EF的最小值为（）

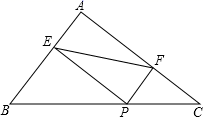A、2 B、2.4 C、3.2 D、3.6

查看试题解析

二、填空题

13. 若式子 $\sqrt{x - 6}$ 在实数范围内有意义，则x的取值范围是.

查看试题解析
14. 若函数y＝kx+b（k≠0）是正比例函数，则b的值为 .

查看试题解析
15.
如图所示，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为

查看试题解析
16. 数学兴趣小组随机调查了“幸福小区”10户家庭一周内使用环保袋的数量，数据如下（单位：个）：6，5，7，8，7，5，8，10，5，9.利用上述数据估计该小区800户家庭一周内需要环保袋共个.

查看试题解析
17. 如图，平行四边形ABCD的周长为20cm，对角线相交于点O，且EO⊥BD于点O交AD于E，则△ABE的周长为cm.

查看试题解析
18. 如图，在△ABC中，∠ACB=90°，M，N分别是AB，AC的中点，延长BC至点D，使CD= $\frac{1}{2}$ BC，连接DM，DN，MN，若AB=6，则DN= ．

查看试题解析

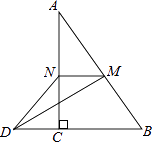
三、解答题

19. 计算：

(1)、 $3 \sqrt{3} (\sqrt{12} + \sqrt{\frac{1}{3}})$ ；

(2)、 $(\sqrt{18} - \sqrt{24}) \div \sqrt{6}$ .

查看试题解析
20. 已知a＝ $\sqrt{5}$ +1，b＝ $\sqrt{5}$ ﹣1，试求a²+2ab+b²的值.

查看试题解析
21. 如图，在锐角三角形ABC中，AB=13，AC =15，点D是BC边上一点，BD =5，AD=12.

(1)、求证：△ADB是直角三角形.

(2)、求BC的长度.

查看试题解析

22. 八（1）班要从李明、张亮两名同学中选拔一人代表班级参加学校举行的跳绳比赛，对他们进行了训练测试（时间：1分钟），他们10次测试的成绩如下：

李明：186，191，196，191，186，201，196，196，211，206；

张亮：172，186，181，191，201，197，201，205，211，215.

制作了如下统计表：

统计量

姓名

平均数

中位数

众数

方差

李明

196

S²

张亮

196

201

164.4

请根据以上信息，解答下列问题：

(1)、直接写出表格中a，b的值；

(2)、求出李明成绩的方差S²；

(3)、请选择合适的统计量作为选拔标准，说明选拔哪一位同学参加学校举行的跳绳比赛.

查看试题解析

23. 某文具店销售功能完全相同的A、B两种品牌的计算器，若购买2个A品牌和3个B品牌的计算器共需156元；购买3个A品牌和1个B品牌的计算器共需122元.

(1)、求这两种品牌计算器的单价；

(2)、开学前夕，该商店对这两种计算器开展了促销活动，具体办法如下：A品牌计算器按原价的八折销售，B品牌计算器超出5个的部分按原价的七折销售，设购买x个A品牌的计算器需婴y₁元，购买x个B品牌的计算器需要y₂元，请分别求出y₁、y₂关于x的函数关系式；

(3)、当需要购买50个计算器时，买哪种品牌的计算器更合算？

查看试题解析
24. 如图，在 $Rt △ A B C$ 中，已知 $∠ A C B = 90 °$ ，过点C的直线 $M N / / A B$ ，D为AB边上一点，过点D作 $D E ⊥ B C$ ，交直线MN于E，垂足为F，连接CD，BE.

(1)、求证： $C E = A D$ ；

(2)、当点D在AB中点时，四边形BECD是什么特殊四边形？说明理由；

(3)、若D为AB的中点，则当 $∠ A$ 的大小满足什么条件时，四边形BECD是正方形？（直接写出结果）

查看试题解析
25. 如图，在平面直角坐标系中，直线 $l$ 与x轴交于点 $A$ （-1，0），与y轴交于点 $B$ （0，-2），点C是x轴正半轴上的一点，且满足CA=CB.

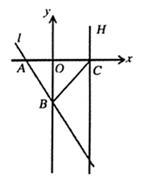(1)、求直线 $l$ 的解析式；

(2)、求点C的坐标和 $△$ ABC的面积；

(3)、过点 $C$ 作 $y$ 轴的平行线 $CH$ ，借助 $△$ $ABC$ 的一边构造与 $△$ $ABC$ 面积相等的三角形，第三个顶点P在直线 $CH$ 上，求出符合条件的点P的坐标.

查看试题解析