广西壮族自治区钦州市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期：2021-09-03 类型：期末考试
一、单选题
-
1. 若 在实数范围内有意义，则a可以是（ ）A、﹣22 B、﹣1 C、 D、02. 某班有六个兴趣小组，人数分别如下：5，6，6，8，9，10，则这组数据的中位数是（ ）A、6 B、7 C、8 D、93. 如图，已知点A表示的数为3，过点A作AB⊥OA于点A，且AB＝2，以O为圆心，OB长为半径作弧，弧与数轴的交点C表示的数是（ ）
A、3.5 B、 C、 D、4. 下列式子能与 合并的是（ ）A、 B、 C、 D、5. 如图，在菱形ABCD中，∠A＝110°，则∠CBD的度数是（ ）
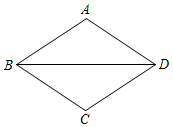A、90° B、70° C、55° D、35°6. 下列说法正确的是（ ）A、形如y＝kx+b（k，b是常数）的函数，叫做一次函数 B、形如y＝kx+b（k，b是常数，b≠0）的函数，叫做一次函数 C、形如y＝kx+1（k是常数，k≠0）的函数，是一次函数 D、形如y＝kx（k是常数，k≠0）的函数，不是一次函数7. 如图是某班全体学生参加体能测试成绩的频数分布直方图（统计中采用“上限不在内”的原则，如成绩为45分统计在45≤x＜50小组，而不在40≤x＜45小组），根据图形提供的信息，下列说法中错误的是（ ）
A、该班学生人数为45人 B、分数在45≤x＜50小组的学生人数占全班人数的20% C、小组40≤x＜45的组中值为42.5 D、该班学生体能测试成绩的中位数落在50≤x＜55这一组8. 如图，点D，E分别是△ABC的边AB，AC的中点，连接BE，过点C作CF∥BE，交DE的延长线于点F，若DE＝ ，则EF的长为（ ）
A、 B、 C、 D、89. 若函数y＝kx（k为常数，且k≠0）的图象经过点A（﹣1，2），则不等式kx≤2的解集为（ ）A、x≥﹣1 B、x≥0 C、x≤0 D、x≤﹣110. 《九章算术》提供了许多整勾股数，如（3，4，5），（5，12，13），（7，24，25）等，并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究，得到如下规律：若m是大于1的奇数，把它平方后拆成相邻的两个整数，那么m与这两个整数构成组勾股数；若m是大于2的偶数，把它除以2后再平方，然后把这个平方数分别减1，加1得到两个整数，那么m与这两个整数构成组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律，“由8生成的勾股数”的“弦数”为（ ）A、16 B、17 C、25 D、6411. 如图，在同一坐标系中，关于x的一次函数y＝x+b与y＝bx+1的图象只可能是（ ）A、
B、
C、
D、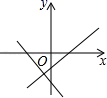
12. 如图，在Rt△ABC中，∠ACB＝90°，AC＝4，AB＝6，分别以AB，AC，BC为边在AB的同侧作正方形ABEF，ACPQ，BCMN，四块阴影部分的面积分别为S1 ， S2 ， S3 ， S4 ， 则S1﹣S2+S3+S4的值是（ ）
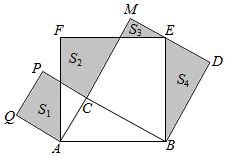A、12 B、24 C、 D、二、填空题
-
13. 计算： = ．14. 一次函数y＝x﹣5的图象与y轴的交点坐标为 .15. 如图是对一组数据进行整理后制成的频数分布表，则这组数据的加权平均数是 .
分组
频数
0≤x＜10
12
10≤x≤20
8
16. 请写出一个y关于x的函数解析式，满足过点（0，2），且y随x的增大而减小 .17. 如图，四边形ABCD是正方形，点E是边BC的中点，∠AEF＝90°，且EF交正方形外角的平分线CF于点F，已知正方形边长为4，则EF的长为 .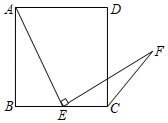
18. 如图，在长50cm，宽40cm，高30cm的木箱内有一只昆虫，如果昆虫要从箱子内的A处沿着箱壁爬行到B处，则它至少要爬 cm.
三、解答题
-
19. 计算：(1)、 ；(2)、 .20. 如图，四边形ABCD是菱形，点E，F分别在边AB，AD上，且AE＝AF，CE＝5，求CF的长.
21. 如图，在四边形ABCD中，已知∠B＝90°，AB＝3，BC＝4，CD＝12，AD＝13，求证AC⊥CD.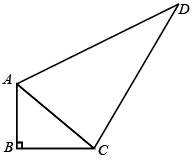
22. 已知一次函数的解析式为y＝mx+2m﹣3（m为常数，m≠0）.(1)、若点（3，﹣2）在一次函数y＝mx+2m﹣3的图象上，求m的值；(2)、若当﹣4≤x≤6时，一次函数y＝mx+2m﹣3（m为常数，m≠0）有最小值﹣5，请求出m的值.23. 刘叔几年前承包了甲，乙两块林地，各栽种100棵李子树，成活率为95%，现已挂果.为分析收成情况，他分别从两块林地随机抽取5棵树作为样本，并采摘完样本树上的李子，每棵树的产量如图所示.
(1)、分别计算甲，乙两块林地样本的平均数；(2)、请根据样本估算甲，乙两块林地李子的总产量；(3)、根据样本，通过计算估计哪块林地的李子产量比较稳定.24. 如图，一艘船从A港沿东南方向航行到C港，然后沿南偏西30°方向航行到B港，此时A港恰好在B港的正北方向，且距离A港30nmile.求B，C两港之间的距离.（结果保留整数，参考数据 ）
25. 振兴加工厂中甲，乙两组工人同时加工某种零件，乙组在工作中有一段时间停产更换设备，更换设备后，乙组的工作效率是原来的2.5倍.两组各自加工零件的数量y（件）与时间x（时）之间的函数图象如图所示.
(1)、求甲组加工零件的数量y与时间x之间的函数解析式；(2)、求出图中a的值及乙组更换设备后加工零件的数量y与时间x之间的函数解析式.26. 如图1，四边形ABCD是正方形，F是BC边上的一点，E是CD边的中点，且AF＝AD+FC，连接EF并延长EF交AD的延长线于点G.
(1)、求证：AE平分∠DAF；(2)、AF＝DE+BF是否成立？若成立，请给出证明，若不成立，请说明理由；(3)、如图2，若四边形ABCD是长与宽不相等的矩形，其他条件不变，试探究上述（1）、（2）中的结论是否成立.请分别做出判断，不需要证明.