广西壮族自治区柳州市2020-2021学年八年级下学期数学期末考试试卷

试卷更新日期：2021-09-03 类型：期末考试

进入出卷网下载

一、单选题

1. 式子 $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、 $x \geq 0$ B、 $x \geq - 2$ C、 $x \leq 2$ D、 $x \geq 2$

查看试题解析
2. 满足a²+b²＝c²的三个正整数称为勾股数，下列各组数为勾股数的是（）

A、2，3，4 B、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{5}$ C、6，7，8 D、5，12，13

查看试题解析

3. 甲、乙，丙、丁四名同学在一次投掷实心球训练中，在相同条件下各投掷10次，他们成绩的平均数与方差s²如下表.若要选一名成绩好且发挥稳定的同学参加比赛，则应选择（）

	甲	乙	丙	丁
平均数 $\bar{x}$ /米	11.1	11.1	10.9	10.9
方差s²/米²	1.1	1.2	1.3	1.4

A、甲 B、乙 C、丙 D、丁

查看试题解析

4. 下面计算正确的是（）

A、4+ $\sqrt{3}$ =4 $\sqrt{3}$ B、 $\sqrt{27}$ ÷ $\sqrt{3}$ =3 C、 $\sqrt{2}$ · $\sqrt{3}$ = $\sqrt{5}$ D、 $\sqrt{4}$ =±2

查看试题解析
5. 函数 $y = k x$ 的图象经过点P（－1，3），则 $k$ 的值为（）

A、3 B、－3 C、 $\frac{1}{3}$ D、－ $\frac{1}{3}$

查看试题解析
6. 在某校“我的中国梦”演讲比赛中，有15名学生参加决赛，他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前8名，不仅要了解自己的成绩，还要了解这15名学生成绩的（）.

A、众数 B、方差 C、平均数 D、中位数

查看试题解析
7. 如图，分别以数轴的单位长度1和3为直角边的长作直角三角形，以数轴上的原点O为圆心，这个直角三角形的斜边为半径作弧与数轴交于一点A，则点A表示的数为（）

A、10 B、3.5 C、2 $\sqrt{2}$ D、 $\sqrt{10}$

查看试题解析
8. 如图，在正方形ABCD的外侧作等边三角形CDE ，则∠DAE的度数为（　　）

A、20° B、15° C、12.5° D、10°

查看试题解析
9. 如图所示，已知点A(﹣1，2)是一次函数y＝kx+b（k≠0）的图象上的一点，则下列判断中正确的是（）

A、y随x的增大而减小 B、k＞0，b＜0 C、当x＜0时，y＜0 D、方程kx+b＝2的解是x＝﹣1

查看试题解析
10. 如图，四边形ABCD中，AC⊥BC ， AD∥BC ， BC＝3，AC＝4，AD＝6．M是BD的中点，则CM的长为（）

A、 $\frac{3}{2}$ B、2 C、 $\frac{5}{2}$ D、3

查看试题解析

二、填空题

11. 计算： ${(2 \sqrt{3})}^{2} =$ .

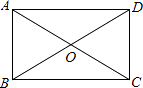
查看试题解析
12. 某单位招聘工作人员，考试分笔试和面试两部分，笔试成绩与面试成绩按6∶4记入总成绩，若小李笔试成绩为90分，面试成绩为80分，则他的总成绩是.

查看试题解析
13. 如图，矩形ABCD的对角线AC=8cm，∠AOD=120°，则AB的长为cm．

查看试题解析
14. 若等边三角形的边长是2cm，则它的高为cm.

查看试题解析
15. 如图，圆柱高8cm，底面半径2cm，一只蚂蚁从点A爬到点B处吃食，要爬行最短路程（π取3）是cm.

查看试题解析
16. 如图1，在平面直角坐标系中，将平行四边形ABCD放置在第一象限，且AB $/ /$ x轴.直线y＝﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2，那么AB的长为.

查看试题解析

三、解答题

17. 计算： $(\sqrt{2} + \sqrt{3}) \times \sqrt{6}$ .

查看试题解析
18. 为了提高学生阅读能力，我区某校倡议八年级学生利用双休日加强课外阅读，为了解同学们阅读的情况，学校随机抽查了部分同学周末阅读时间，并且得到数据绘制了不完整的统计图，根据图中信息回答下列问题：

(1)、本次调查的总人数为人，将条形统计图补充完整；

(2)、被调查的学生周末阅读时间众数是小时；

(3)、该校八年级共有500人，试估计周末阅读时间不低于1.5小时的人数.

查看试题解析
19. 如图在平行四边形ABCD的对角线AC的延长线上取两点E、F，使EA＝CF，求证：四边形EBFD是平行四边形.

查看试题解析
20. 已知等腰三角形的周长为6.

(1)、写出底边长y关于腰长x的函数解析式（x为自变量）；

(2)、求自变量x的取值范围；

(3)、在直角坐标系中，画出函数图象.

查看试题解析
21. 已知直线y＝kx+b经过点A（5，0），B（1，4）.

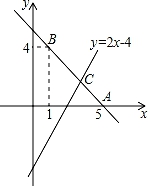(1)、求直线AB的解析式；

(2)、若直线y＝2x﹣4与直线AB相交于点C，求点C的坐标；

(3)、根据图象，写出关于x的不等式2x﹣4＞kx+b的解集.

查看试题解析
22. 如图，在四边形ABCD中，AB $//$ DC ， AB=AD ，对角线AC ， BD交于点O ， AC平分∠BAD ，过点A作AM⊥CB交CB的延长线于点M ，连接OM ．

(1)、求证：四边形ABCD是菱形；

(2)、若BC= $\sqrt{5}$ ，BD=2，求OM的长．

查看试题解析
23. 如图，直线y＝ $\frac{2}{3}$ x+4分别交x轴，y轴于点B，点A.

(1)、求点A，点B的坐标；

(2)、平移直线AB，交x轴正半轴于点E，交y轴于点F，P为直线EF上的第三象限内的一点，过点P作PG⊥x轴于点G，若 $S_{△ P A B}$ ＝20，且GE＝12，求点P的坐标.

查看试题解析