广西壮族自治区来宾市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-09-03 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 一个多边形的内角和是外角和的3倍,则这个多边形是( )A、六边形 B、七边形 C、八边形 D、九边形3. 下列平面直角坐标系中的图象,不能表示y是x的函数的是( )A、
2. 一个多边形的内角和是外角和的3倍,则这个多边形是( )A、六边形 B、七边形 C、八边形 D、九边形3. 下列平面直角坐标系中的图象,不能表示y是x的函数的是( )A、 B、
B、 C、
C、 D、
D、 4. 对某中学70名女生的身高进行测量,得到一组数据的最大值为169 cm,最小值为143 cm,对这组数据整理时测定它的组距为5 cm,应分成( )A、5组 B、6组 C、7组 D、8组5. 平行四边形的对角线一定具有的性质是( )A、相等 B、互相平分 C、互相垂直 D、互相垂直且相等6. 如果一次函数y=﹣2x+1的图象经过点(﹣1,m),则m的值是( )A、﹣3 B、﹣1 C、1 D、37. 如图,菱形ABCD中,∠D=140°,则∠1的大小是( )
4. 对某中学70名女生的身高进行测量,得到一组数据的最大值为169 cm,最小值为143 cm,对这组数据整理时测定它的组距为5 cm,应分成( )A、5组 B、6组 C、7组 D、8组5. 平行四边形的对角线一定具有的性质是( )A、相等 B、互相平分 C、互相垂直 D、互相垂直且相等6. 如果一次函数y=﹣2x+1的图象经过点(﹣1,m),则m的值是( )A、﹣3 B、﹣1 C、1 D、37. 如图,菱形ABCD中,∠D=140°,则∠1的大小是( ) A、10° B、20° C、30° D、40°8. 如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )
A、10° B、20° C、30° D、40°8. 如图,已知AD是△ABC的BC边上的高,下列能使△ABD≌△ACD的条件是( )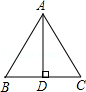 A、AB=AC B、∠BAC=90° C、BD=AC D、∠B=45°9. 如果一次函数y=kx+b的函数值y随x的增大而减小,那么函数y=kx﹣1的图象可能是( )A、
A、AB=AC B、∠BAC=90° C、BD=AC D、∠B=45°9. 如果一次函数y=kx+b的函数值y随x的增大而减小,那么函数y=kx﹣1的图象可能是( )A、 B、
B、 C、
C、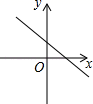 D、
D、 10. 如图,若菱形ABCD的顶点A、B的坐标分别为(3,0)、(﹣2,0),点D在y轴上,则点C的坐标是( )
10. 如图,若菱形ABCD的顶点A、B的坐标分别为(3,0)、(﹣2,0),点D在y轴上,则点C的坐标是( ) A、(﹣5,4) B、(﹣5,5) C、(﹣4,4) D、(﹣4,5)11. 如图,直线y=2x+b(b>0)与x,y轴分别交于A,B两点,以OB为斜边在y轴右侧作等腰直角三角形OBC,将点C向左平移,使其对应点C恰好落在直线AB上,若OC=2 ,则点 的坐标为( )
A、(﹣5,4) B、(﹣5,5) C、(﹣4,4) D、(﹣4,5)11. 如图,直线y=2x+b(b>0)与x,y轴分别交于A,B两点,以OB为斜边在y轴右侧作等腰直角三角形OBC,将点C向左平移,使其对应点C恰好落在直线AB上,若OC=2 ,则点 的坐标为( )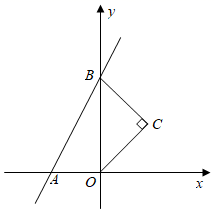 A、(﹣1,2) B、(﹣1, ) C、(﹣2,2) D、(﹣1,2 )12. 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )
A、(﹣1,2) B、(﹣1, ) C、(﹣2,2) D、(﹣1,2 )12. 如图,在矩形ABCD中,边AB的长为3,点E,F分别在AD,BC上,连接BE,DF,EF,BD.若四边形BEDF是菱形,且EF=AE+FC,则边BC的长为( )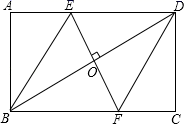 A、2 B、3 C、6 D、
A、2 B、3 C、6 D、二、填空题
-
13. 已知一组数据有40个,把它分成六组,第一组到第四组的频数分别是10,5,7,6,第五组的频率是0.2,则第六组的频率是
14. 如图,在平行四边形ABCD中,在不添加任何辅助线的情况下,请添加一个条件 , 使平行四边形ABCD是矩形. 15. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,AC=8,BD=6,点E是CD的中点,连接OE,则OE的长是.
15. 如图,四边形ABCD是菱形,对角线AC、BD相交于点O,AC=8,BD=6,点E是CD的中点,连接OE,则OE的长是. 16. 如图,在四边形ABCD中,点E、F、G、H分别是AB、BC、CD、DA的中点,AC⊥BD,AC=BD,则四边形EFGH是.
16. 如图,在四边形ABCD中,点E、F、G、H分别是AB、BC、CD、DA的中点,AC⊥BD,AC=BD,则四边形EFGH是. 17. 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向航行60海里到达点A处,同一时刻渔船已航行到与港口O相距80海里的点B处,若A、B两点相距100海里,则渔船在港口南偏西°的方向.
17. 一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向航行60海里到达点A处,同一时刻渔船已航行到与港口O相距80海里的点B处,若A、B两点相距100海里,则渔船在港口南偏西°的方向.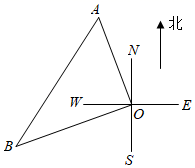 18. 如图,在边长为4的正方形ABCD中,点E在AD上,且AE=1,P为对角线BD上的一个动点,则 APE周长的最小值是.
18. 如图,在边长为4的正方形ABCD中,点E在AD上,且AE=1,P为对角线BD上的一个动点,则 APE周长的最小值是.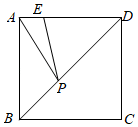
三、解答题
-
19. 如图,在 ABC中,∠C=90°,∠B=30°,AD是∠BAC的角平分线.若AD=4,求AB的长.
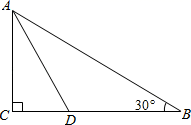 20. 如图,在平面直角坐标系中, ABC的顶点坐标分别为A(1,1),B(4,﹣2),C(3,3).
20. 如图,在平面直角坐标系中, ABC的顶点坐标分别为A(1,1),B(4,﹣2),C(3,3). (1)、画出 ABC关于y轴对称的 A1B1C1 , 并写出顶点B1的坐标;(2)、画出 ABC关于原点对称的 A2B2C2;(3)、试判断 ABC是否是直角三角形,并说明理由.21. 某校为提高学生的安全意识,组织全校1200名学生参加安全知识竞赛,从中抽取了部分学生成绩(分数为正整数,满分100分)进行统计,并制作不完全统计图表:
(1)、画出 ABC关于y轴对称的 A1B1C1 , 并写出顶点B1的坐标;(2)、画出 ABC关于原点对称的 A2B2C2;(3)、试判断 ABC是否是直角三角形,并说明理由.21. 某校为提高学生的安全意识,组织全校1200名学生参加安全知识竞赛,从中抽取了部分学生成绩(分数为正整数,满分100分)进行统计,并制作不完全统计图表:分数段
频数
频率
50≤x<60
20
0.1
60≤x<70
40
0.2
70≤x<80
70
0.35
80≤x<90
m
0.3
90≤x<100
10
n

请根据所给数据解答下列问题:
(1)、这次共抽取了名学生的竞赛成绩进行统计,其中:m= , n=;(2)、补全频数分布直方图;(3)、若成绩在70分以下(不含70分)视为安全意识不强,有待进一步加强安全教育,请估计全校安全意识不强的学生人数.22. 如图,直线l1:y=x+1与直线l2:y=mx+n相交于点P(1,b). (1)、求b的值;(2)、不解关于x、y的方程组 ,请你直接写出它的解;(3)、直线l3:y=nx+m是否也经过点P?请说明理由.23. 如图,在正方形ABCD中,点P在AD上,且不与A,D重合,点H在AB上,且不与A,B重合,连接BP、CH,BP与CH交于点E.
(1)、求b的值;(2)、不解关于x、y的方程组 ,请你直接写出它的解;(3)、直线l3:y=nx+m是否也经过点P?请说明理由.23. 如图,在正方形ABCD中,点P在AD上,且不与A,D重合,点H在AB上,且不与A,B重合,连接BP、CH,BP与CH交于点E. (1)、若BP=CH,求证:BP⊥CH;(2)、在(1)的条件下,若正方形ABCD的边长为12,AP=5,求线段CE的长.24. 某商店计划采购甲、乙两种不同型号的平板电脑共30台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价2500元,售价3000元.(1)、设该商店采购甲型平板电脑x台,请写出全部售出后该商店获利y与x之间函数解析式;(2)、若该商店采购两种平板电脑的总费用不超过60000元,全部售出所获利润不低于12500元,问共有几种采购方案,并求出使商店获得最大利润的采购方案及最大利润.25. 如图,在 中,点O是 边上的一个动点,过点O作直线 ,设 交 的角平分线于点E,交 的外角 的平分线于点F,连接 .
(1)、若BP=CH,求证:BP⊥CH;(2)、在(1)的条件下,若正方形ABCD的边长为12,AP=5,求线段CE的长.24. 某商店计划采购甲、乙两种不同型号的平板电脑共30台,已知甲型平板电脑进价1600元,售价2000元;乙型平板电脑进价2500元,售价3000元.(1)、设该商店采购甲型平板电脑x台,请写出全部售出后该商店获利y与x之间函数解析式;(2)、若该商店采购两种平板电脑的总费用不超过60000元,全部售出所获利润不低于12500元,问共有几种采购方案,并求出使商店获得最大利润的采购方案及最大利润.25. 如图,在 中,点O是 边上的一个动点,过点O作直线 ,设 交 的角平分线于点E,交 的外角 的平分线于点F,连接 .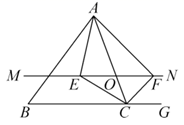 (1)、求证: ;(2)、当点O运动到何处时,四边形 是矩形?并证明你的结论.(3)、在(2)的条件下, 满足什么条件时,四边形 是正方形?并说明理由.26. 如图,在平面直角坐标系中,平行四边形OABC的顶点A、C坐标分别为(2,0),(1,2).
(1)、求证: ;(2)、当点O运动到何处时,四边形 是矩形?并证明你的结论.(3)、在(2)的条件下, 满足什么条件时,四边形 是正方形?并说明理由.26. 如图,在平面直角坐标系中,平行四边形OABC的顶点A、C坐标分别为(2,0),(1,2). (1)、直接写出点B的坐标,并求出直线AC的解析式;(2)、若D是直线AC上的一个动点(D与A、C不重合),当 DBC的面积是3时,请求出点D的坐标;(3)、在y轴上是否存在一点P,使得 PAC是不以点P为直角顶点的直角三角形.若存在,请求出P的坐标,若不存在,请说明理由.
(1)、直接写出点B的坐标,并求出直线AC的解析式;(2)、若D是直线AC上的一个动点(D与A、C不重合),当 DBC的面积是3时,请求出点D的坐标;(3)、在y轴上是否存在一点P,使得 PAC是不以点P为直角顶点的直角三角形.若存在,请求出P的坐标,若不存在,请说明理由.