广西壮族自治区河池市宜州区2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期:2021-09-03 类型:期末考试
一、单选题
-
1. 计算 的结果是( )A、 B、2 C、 D、42. 下列各组线段能构成直角三角形的一组是( )A、1,1, B、2,3,4 C、2,4,5 D、6,8,123. 下列是最简二次根式的是( )A、 B、 C、 D、4. 下列变量之间是函数关系的有( )
①正方形的周长C与边长a;②矩形的周长C与宽a;③圆的面积S与半径R;④y=2x-3中的y与x
A、4个 B、3个 C、2个 D、1个5. 在平行四边形ABCD中,∠A:∠B:∠C:∠D可以是( )A、2:3:4:5 B、3:2:3:2 C、2:2:1:1 D、2:3:3:26. 关于一组数据的平均数、中位数、众数,下列说法中正确的是( )A、平均数一定是这组数中的某个数 B、中位数一定是这组数中的某个数 C、众数一定是这组数中的某个数 D、中位数一定是众数7. 下列命题中,是真命题的是( )A、四个角都是直角的四边形是正方形 B、对角线相等的四边形是矩形 C、对角线相等的平行四边形是正方形 D、菱形的对角线互相垂直8. 下列各图象中,不表示 是 的函数的是( )A、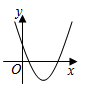 B、
B、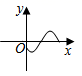 C、
C、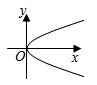 D、
D、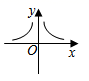 9. 一组数据1,x,5,7的中位数与众数相等,则该组的平均数是( )A、3.5 B、4.5 C、5.5 D、610. 若正比例函数图象过点(1,-2),则下列说法不正确的是( )A、函数值随自变量的增大而增大 B、函数值随自变量的增大而减小 C、函数图象过点(2,-4) D、函数图象过二、四象限11. 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点 的位置, 与CD交于点E,若AB=8,AD=2,则图中阴影部分的周长为( )
9. 一组数据1,x,5,7的中位数与众数相等,则该组的平均数是( )A、3.5 B、4.5 C、5.5 D、610. 若正比例函数图象过点(1,-2),则下列说法不正确的是( )A、函数值随自变量的增大而增大 B、函数值随自变量的增大而减小 C、函数图象过点(2,-4) D、函数图象过二、四象限11. 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落到点 的位置, 与CD交于点E,若AB=8,AD=2,则图中阴影部分的周长为( ) A、20 B、14 C、10 D、12. 如图,在正方形ABCD中,BC=3,延长CD至点E,使得DE=1,EF⊥CE,EF=CE,连接AF、CF,若G为AF的中点,则CG的长为( )
A、20 B、14 C、10 D、12. 如图,在正方形ABCD中,BC=3,延长CD至点E,使得DE=1,EF⊥CE,EF=CE,连接AF、CF,若G为AF的中点,则CG的长为( ) A、3 B、 C、 D、
A、3 B、 C、 D、二、填空题
-
13. 比较大小: .14. 函数y= 中,自变量x的取值范围是 .15. 已知2,3,6,a,b这五个数据的方差是3,那么3,4,7,a+1,b+1这五个数据的方差是.16. 《九章算术》中的“引葭赴岸”问题:今有池方一丈,葭(一种芦苇类植物)生其中央,出水一尺.引葭赴岸,适与岸齐,水深几何?其大意是:有一个边长为10尺的正方形池塘,一棵芦苇生长在它的正中央,高出水面1尺.如果把该芦苇拉向岸边,那么芦苇的顶部恰好碰到岸边(如图所示),则水深尺.
 17. 如图, ABC中,∠ACB=90°,AD平分∠BAC,AB=5,AC=3,则CD的长是.
17. 如图, ABC中,∠ACB=90°,AD平分∠BAC,AB=5,AC=3,则CD的长是. 18. 在 中, 边上的高线为12,则 的面积为.
18. 在 中, 边上的高线为12,则 的面积为.三、解答题
-
19. 计算:20. 如图,平面直角坐标系中,函数y=kx+2的图象过点A(3,0),将其图象向上平移2个单位后与x轴交于点B,与y轴交于点C.
 (1)、求k的值;(2)、图象经过点B和C的函数解析式为;(3)、 OBC的面积为.21. 已知x满足 ,求 的值.
(1)、求k的值;(2)、图象经过点B和C的函数解析式为;(3)、 OBC的面积为.21. 已知x满足 ,求 的值.解:由 有意义可知x的取值范围是_▲_
∵
∴_▲_+ (去掉绝对值符号)
∴ _▲_ (移项,合并)
∴ _▲_ (算术平方根的意义)
∴ _▲_
22. 如图,已知 ABCD中,E、F分别是AD、BC边上的点,DE=BF,求证:AF CE. 23. 如图, ABCD的两条对角线交于点O, AOB是等边三角形.
23. 如图, ABCD的两条对角线交于点O, AOB是等边三角形. (1)、求证:四边形ABCD是矩形;(2)、若OE⊥BD交BC于E,CE=2,则AD= .24. “五四”青年节前夕,学校为每个班都拍摄了若干张风格迥异的集体照,由各同学自行选择留作纪念.为了解同学们对集体照的选择情况,全校进行了一次抽样调查,按照同学们选择的张数把选择情况分为四个层次:A:4张;B:3张;C:2张;D:1张.并将调查结果绘制成了条形统计图和扇形统计图,请结合图中信息解答下列问题:
(1)、求证:四边形ABCD是矩形;(2)、若OE⊥BD交BC于E,CE=2,则AD= .24. “五四”青年节前夕,学校为每个班都拍摄了若干张风格迥异的集体照,由各同学自行选择留作纪念.为了解同学们对集体照的选择情况,全校进行了一次抽样调查,按照同学们选择的张数把选择情况分为四个层次:A:4张;B:3张;C:2张;D:1张.并将调查结果绘制成了条形统计图和扇形统计图,请结合图中信息解答下列问题:
 (1)、抽样调查的学生总人数为(人);(2)、补全条形统计图和扇形统计图;(3)、根据调查结果,估计全校2000名同学一共选择了多少张集体照?25. 学校决定采购一批气排球和篮球,已知购买2个气排球和2个篮球共需340元,购买2个气排球所需费用比购买2个篮球所需费用少140元.(1)、求气排球和篮球的售价分别是多少(元/个)?(2)、学校计划购进气排球和篮球共120个,其中气排球的数量不超过篮球数量的3倍,若设购买篮球x个,当x为何值时总费用最小,并说明理由.26. 某山区的甲乙两地相距240km,一辆货车从甲地出发匀速开往乙地,货车出发2小时后,一辆小汽车从乙地出发匀速开往甲地,两车同时到达各自的目的地.已知两车行驶的路程之和y(km)与货车行驶的时间x(h)之间的函数关系如图所示.
(1)、抽样调查的学生总人数为(人);(2)、补全条形统计图和扇形统计图;(3)、根据调查结果,估计全校2000名同学一共选择了多少张集体照?25. 学校决定采购一批气排球和篮球,已知购买2个气排球和2个篮球共需340元,购买2个气排球所需费用比购买2个篮球所需费用少140元.(1)、求气排球和篮球的售价分别是多少(元/个)?(2)、学校计划购进气排球和篮球共120个,其中气排球的数量不超过篮球数量的3倍,若设购买篮球x个,当x为何值时总费用最小,并说明理由.26. 某山区的甲乙两地相距240km,一辆货车从甲地出发匀速开往乙地,货车出发2小时后,一辆小汽车从乙地出发匀速开往甲地,两车同时到达各自的目的地.已知两车行驶的路程之和y(km)与货车行驶的时间x(h)之间的函数关系如图所示. (1)、货车的速度是km/h,a的值为 , 小汽车行驶了小时到达甲地;(2)、求小汽车出发后y与x之间的函数关系式,并写出b的值;(3)、当两车相距100km时,求货车行驶的时间.
(1)、货车的速度是km/h,a的值为 , 小汽车行驶了小时到达甲地;(2)、求小汽车出发后y与x之间的函数关系式,并写出b的值;(3)、当两车相距100km时,求货车行驶的时间.