广西壮族自治区百色市2020-2021学年八年级下学期数学期末考试试卷
试卷更新日期：2021-09-03 类型：期末考试
一、单选题
-
1. 下列式子是最简二次根式的是（ ）A、 B、2 C、 D、32. 六边形外角和等于（ ）A、180° B、360° C、420° D、480°3. 下列二次根式中，与 是同类二次根式是（ ）A、 B、 C、 D、4. 在一组数据1，3，7，5，9中，中位数是（ ）A、1 B、3 C、5 D、75. 已知关于x的一元二次方程x2＋mx﹣3＝0有一个根为1，则m的值为（ ）A、﹣1 B、1 C、﹣2 D、26. 下列几组数据能作为直角三角形的三边长的是( )A、2，3，4 B、5，3，4 C、4，6，9 D、5，11，137. 学校组织“热爱祖国”演讲比赛，小娜演讲内容得90分，语言表达得88分，若按演讲内容占60%、语言表达占40%的比例计算总成绩，则小娜的总成绩是（ ）A、90分 B、88分 C、89分 D、89.2分8. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩都为9环，方差分别为S甲2＝0.29，S乙2＝0.32，S丙2＝0.25，S丁2＝0.36，则四人中成绩最稳定的是（ ）A、甲 B、乙 C、丙 D、丁9. 一种药品原价每盒25元，经过两次降价后每盒16元设两次降价的百分率都为x，则x满足（ ）A、 B、 C、 D、10. 有40个数据，其中最大值为35，最小值为15，若取组距为4，则应该分的组数是（ ）A、5 B、6 C、7 D、811. 如图，在Rt△ABC中，∠ABC＝90°，BC＝8cm，AB＝6cm，D为AC的中点，则BD的长为（ ）
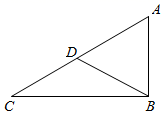A、4cm B、5cm C、6cm D、6.5cm12. 如图，将正方形OABC放在平面直角坐标系中，O是原点，点A的坐标为(1， )，则点C的坐标为（ ）
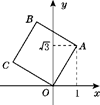A、(－ ，1) B、(－1， ) C、( ，1) D、(－ ，－1)二、填空题
-
13. 若二次根式 在实数范围内有意义，则x的取值范围是 ．
14. 一元二次方程x2﹣2x﹣8＝0的常数项是 .15. “植树节”时，九年级一班6个小组的植树棵数分别是：5，7，3，x，6，4．已知这组数据的众数是5，则该组数据的平均数是.
16. 如图，在菱形ABCD中，对角线AC与BD交于点O，点E是BC边的中点，OE＝1，则BC的长为.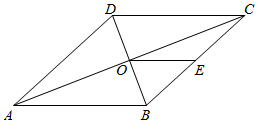
17. 如图，点E在正方形ABCD内，AE＝6，BE＝8，AB＝10，则阴影部分的面积为.
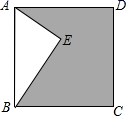18. 如图所示为一个按某种规律排列的数阵：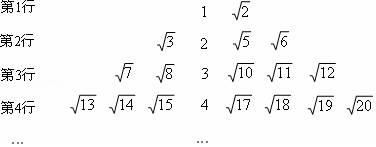
根据数阵的规律，第7行倒数第二个数是 ．
三、解答题
-
19. 计算： ﹣ ＋| ﹣2|＋ .20. 解方程：x2＋2x-15＝0.21. 如图，▱ABCD的对角线AC、BD交于点O，E、F是对角线AC上两点，AE＝CF.求证：四边形DEBF是平行四边形.
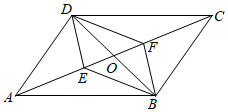22. 关于x的一元二次方程x2﹣3x＋k＝0有实数根.(1)、求k的取值范围；(2)、若k是符合条件的最大整数，求此时一元二次方程的解.23. 某中学数学小组为了解本社区居民对“新型冠状病毒”防疫的重视程度，在社区内随机抽取部分居民进行调查.根据调查结果，把防疫的重视程度分成“淡薄”“一般”“较强”“很强”四个层次，并绘制成两个不完整的统计图.
请结合图表中的信息，解答下列问题：
(1)、此次调查一共随机抽取了名居民；(2)、请将条形统计图补充完整；(3)、扇形统计图中，“很强”所对应扇形圆心角的度数为.(4)、若该社区有1800人，则可以估计该社区居民对防疫的重视程度为“淡薄”层次的约有多少人？24. 如图，依靠一面长18米的墙，用34米长的篱笆围成一个矩形场地花圃ABCD，AB边上留有2米宽的小门EF（用其他材料做，不用篱笆围）.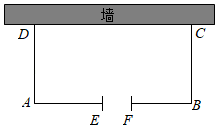
(1)、设花圃的一边AD长为x米，请你用含x的代数式表示另一边CD的长为 米；(2)、当矩形场地面积为160平方来时，求AD的长.25. 已知：如图，在四边形ABCD中，∠BAC＝∠ACD＝90°，AB＝ CD，点E是CD的中点.
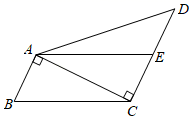(1)、求证：AE＝BC；(2)、若AC＝4，AD＝4 ，求四边形ABCE的面积.26. 在矩形ABCD中，AB＝6cm，BC＝10cm，点P从点B出发，以2cm/s的速度沿BC向点C运动，如图①，设点P的运动时间为t（t≤5）秒.
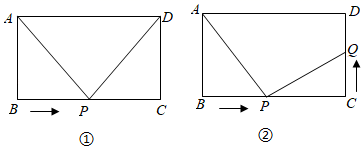(1)、PC＝cm（用含t的代数式表示）；(2)、当t为何值时，△ABP≌△DCP？请说明理由；(3)、如图②，当点P从点B开始运动的同时，点Q从点C出发，以vcm/s的速度沿CD向点D运动（Q到达D点即停），是否存在这样的v，使△ABP与P、Q、C三点围成的三角形全等？若存在，请求出v的值；若不存在，请说明理由.