广西壮族自治区南宁市宾阳县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-03 类型：期中考试

进入出卷网下载

一、单选题

1. 下列图形中，成中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 用配方法解方程 $x^{2} - 2 x - 1 = 0$ 时，配方后所得的方程为（）

A、 $（ x + 1 ）^{2} = 0$ B、 $（ x - 1 ）^{2} = 0$ C、 $（ x + 1 ）^{2} = 2$ D、 $（ x - 1 ）^{2} = 2$

查看试题解析
3. 今年新型冠状病毒肆虐，它的直径为 $1.25 \times 10^{- 7} m$ ，则 $1.25 \times 10^{- 7}$ 的原数是（）

A、0.0000125 B、0.00000125 C、0.000000125 D、0.0000000125

查看试题解析
4. 一种药品原价每盒25元，经过两次降价后每盒16元，设两次降价的百分率都为x，则x满足等式（）

A、 $16 {(1 + x)}^{2} = 25$ B、 $16 {(1 - x)}^{2} = 25$ C、 $25 {(1 - x)}^{2} = 16$ D、 $25 {(1 + x)}^{2} = 16$

查看试题解析
5. 方程x²+4x+4＝0的根的情况是（）

A、有两个不相等的实数根 B、有两个相等的实数根 C、有一个实数根 D、没有实数根

查看试题解析
6. 若m是方程 $x^{2} - 2 x - 1 = 0$ 的根，则 $1 + 2 m - m^{2}$ 的值为（）

A、0 B、1 C、-1 D、2

查看试题解析
7. 抛物线y＝x²﹣4x+2不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 如图，线段AB绕着点O旋转一定的角度得线段A'B'，下列结论错误的是（）

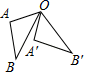A、AB＝A'B' B、∠AOA'＝∠BOB' C、OB＝OB' D、∠AOB'＝100°

查看试题解析
9. 函数y=﹣2x²先向右平移1个单位，再向下平移2个单位，所得函数解析式是（）

A、y=﹣2（x﹣1）²+2 B、y=﹣2（x﹣1）²﹣2 C、y=﹣2（x+1）²+2 D、y=﹣2（x+1）²﹣2

查看试题解析
10. 对于抛物线y＝（x﹣1）²+2的描述正确的是（）

A、开口向下 B、顶点坐标为（﹣1，2） C、有最大值为2 D、对称轴为x＝1

查看试题解析
11. 如图，将△ABC绕点C顺时针旋转，点B的对应点为点E，点A的对应点为点D，当点E恰好落在边AC上时，连接AD，若∠ACB=30°，则∠DAC的度数是（）

A、 $60^{\circ}$ B、 $65^{\circ}$ C、 $70^{\circ}$ D、 $75^{\circ}$

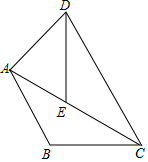查看试题解析
12. 如图，二次函数 $y = a x^{2} + b x + c (a \neq 0)$ 的图象与x轴交于A、B两点，与y轴交于点C，且OC＝2OB则下列结论：① $a b c < 0$ ；② $a + b + c > 0$ ；③ $a c - 2 b + 4 = 0$ ；④ $O A \cdot O B = - \frac{c}{a}$ ，其中正确的结论有（）

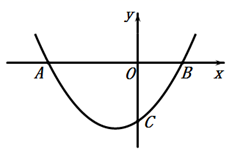A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 写出有一个根为1的一元二次方程是.

查看试题解析
14. 平面直角坐标系中，点 $(2 ， - 4)$ 关于原点O的对称点的坐标是.

查看试题解析
15. 如图，对称轴平行于y轴的抛物线与x轴交于（2，0），（6，0）两点，则它的对称轴为.

查看试题解析
16. 如图，△ABC中，∠BAC＝90°，AB＝AC，△ABC绕着点A按逆时针方向旋转一个角度后，得到△ACD，则图中的旋转角等于度

查看试题解析
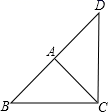17. 把二次函数 $y = {(x - 1)}^{2} + 2$ 的图象绕原点旋转180°后得到的图象解析式为．

查看试题解析
18. 如图抛物线 $y = 2 x^{2} + 4 x - 6$ 与x轴交于A，B两点，与y轴交于点C，点P是抛物线对称轴上任意一点，若点D、E、F分别是BC、BP、PC的中点，连接DE，DF，则DE+DF的最小值为.

查看试题解析

三、解答题

19. 计算： ${(- 1)}^{2020} + 10 \div 4 \times \frac{1}{2} - \sqrt{9}$ .

查看试题解析
20. 解方程： $x (2 x - 5) = 4 x - 10$

查看试题解析
21. 如图，正方形ABCD ，点E ， F分别在AD ， CD上，且DE＝CF ， AF与BE相交于点G ．

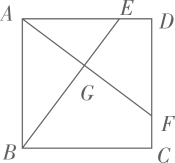(1)、求证：BE＝AF；

(2)、若AB＝4，DE＝1，求AG的长．

查看试题解析
22. 如图，在平面直角坐标系中，△ABC的三个顶点分别是A（1，1），B（4，1），C（3，3）.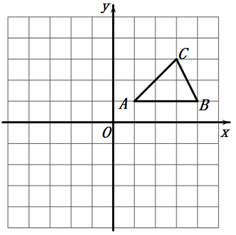

（ 1 ）请画出△ABC关于原点O成中心对称的△A₁B₁C₁；

（ 2 ）将△ABC绕点A按逆时针方向旋转90°得到△AB₂C₂ ，请画出旋转后的△AB₂C₂；

（ 3 ）在图中找到一点D，使得A、B、C、D四点围成一个以AC、BC为邻边的平行四边形，请画出这个平行四边形，并写出点D的坐标.

查看试题解析
23. 某口罩生产厂生产的口罩1月份平均日产量为30000个，1月底因突然爆发新冠肺炎疫情，市场对口罩需求量大增，为满足市场需求，厂决定从2月份起扩大产量，3月份平均日产量达到36300个.

(1)、求口罩日产量的月平均增长率；

(2)、按照这个增长率，预计4月份平均日产量为多少？

查看试题解析
24. 某厂生产一种玩具，成本价是8元∕件，经过调查发现，每天的销售量y（件）与销售单价x（元）存在一次函数关系 $y = - 10 x + 600$ .

(1)、销售单价定为多少时，该厂每天获得的利润最大？最大利润是多少？

(2)、若物价部门规定，该产品的最高销售单价不得超过30元，那么销售单价如何定位才能获得最大利润？

查看试题解析
25. （探索发现）如图①，四边形ABCD是正方形，M，N分别在边CD、BC上，且 $∠ MAN= 45 °$ ，我们把这种模型称为“半角模型”，在解决“半角模型”问题时，旋转是一种常用的方法.如图①，将 $Δ A D M$ 绕点A顺时针旋转 $90 °$ ，点D与点B重合，得到 $Δ A B E$ ，连接AM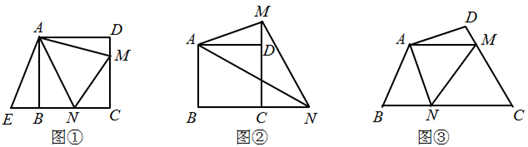、AN、MN.

(1)、试判断DM，BN，MN之间的数量关系，并写出证明过程.

(2)、如图②，点M、N分别在正方形ABCD的边BC、CD的延长线上， $∠ MAN= 45 °$ ，连接MN，请写出MN、DM、BN之间的数量关系，并写出证明过程.

(3)、如图③，在四边形ABCD中，AB=AD， $∠ BAD= 120 °$ ， $∠ B+ ∠ D= 180 °$ ，点N，M分别在边BC，CD上， $∠ MAN= 60 °$ ，请直接写出线段BN，DM，MN之间的数量关系.

查看试题解析
26. 如图，抛物线 $y = a x {}^{2}- \frac{1}{3} x + c$ 交于x轴于 $A (- 3 ， 0)$ ，B两点，与 $y$ 轴交于点 $C (0 ， - 4)$ ，连接AC、BC，M为线段OB上的一个动点，过点M作PM⊥x轴，交抛物线于点P，交BC于点Q.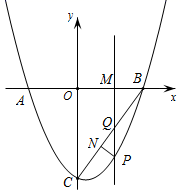

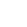
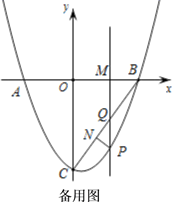(1)、求抛物线的解析式.

(2)、过点P作PN⊥BC，垂足为点N，设M点坐标为 $M (m ， 0)$ ，请用含m的代数式表示线段PN的长，并求出当m为何值时PN有最大值，最大值是多少？

(3)、试探究点M在运动过程中，是否存在这样的点Q使得以A、C、Q为顶点的三角形是等腰三角形，若存在，请求出此时点Q的坐标；若不存在.请说明理由.

查看试题解析