广西壮族自治区桂林市全州县2020-2021学年九年级上学期数学期中考试试卷

试卷更新日期：2021-09-03 类型：期中考试

进入出卷网下载

一、单选题

1. 已知点P(-2，3)在反比例函数 $y = \frac{k}{x}$ 上，则 $k$ 的值等于（）

A、1 B、-6 C、-1 D、6

查看试题解析
2. 下列方程中，是关于 $x$ 的一元二次方程的是（）

A、 $x^{2} + \frac{1}{x^{2}} = 0$ B、 $a x^{2} + b x + c = 0$ C、 $(x - 1) (x + 2) = 1$ D、 $3 x^{_{2}} + 3 x - 5$

查看试题解析
3. 如果2是方程x²-3x+k=0的一个根，则常数k的值为（）．

A、2 B、1 C、-1 D、-2

查看试题解析
4. 用公式法解 $x^{2} + 3 x = 1$ 时，先求出a、b、c的值，则a、b、c依次为（）.

A、1，3，1 B、1，3，-1 C、-1，-3，-1 D、-1，3，1

查看试题解析
5. 若关于 $x$ 的一元二次方程 $k x^{2} - 6 x + 9 = 0$ 有两个不相等的实数根，则 $k$ 的取值范围（）

A、 $k < 1$ 且 $k \neq 0$ B、 $k \neq 0$ C、 $k < 1$ D、 $k > 1$

查看试题解析
6. 若y=（5+m）x²⁺ⁿ是反比例函数，则m、n的取值是（　　）

A、m=﹣5，n=﹣3 B、m≠﹣5，n=﹣3 C、m≠﹣5，n=3 D、m≠﹣5，n=﹣4

查看试题解析
7. 已知△ABC∽△DEF，且相似比为1：2，则△ABC与△DEF的面积比为（）

A、1：4 B、4：1 C、1：2 D、2：1

查看试题解析
8. 已知关于x的方程x²+mx﹣6=0的一个根为2，则m的值及另一个根是（）

A、1，3 B、﹣1，3 C、1，﹣3 D、﹣1，﹣3

查看试题解析
9. 某地图上1cm²面积表示实际面积900m² ，则该地图的比例尺是（）

A、 $1 ： 30$ B、 $1 ： 3000$ C、 $1 ： 900$ D、 $1 ： 90000000$

查看试题解析
10. 如图，已知AB、CD、EF都与BD垂直，垂足分别是B、D、F，且AB＝1，CD＝3，那么EF的长是（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{3}{4}$ D、 $\frac{4}{5}$

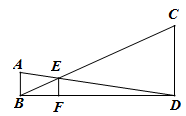查看试题解析
11. 如图，△ABC中，DF∥EG∥BC，且AD＝DE＝EB，则△ABC被分成的三部分的面积比S_Ⅰ∶S_Ⅱ∶S_Ⅲ为（）

A、1∶1∶1 B、1∶3∶5 C、1∶2∶3 D、1∶4∶9

查看试题解析
12. 如图，在平行四边形ABCD中，AC = 4，BD = 6，P是BD上的任一点，过P作EF∥AC，与平行四边形的两条边分别交于点E，F.设BP=x，EF=y，则能大致反映y与x之间关系的图象为（）

A、 B、 C、 D、

查看试题解析

二、填空题

13. 反比例函数 $y = - \frac{2}{x}$ 的比例系数是 .

查看试题解析
14. 若关于 $x$ 的一元二次方程 $x^{2} - 4 x + k = 0$ 有两个相等的实数根，则 $k =$ .

查看试题解析
15. 如图，AB∥CD，AD与BC相交于点O，若AO=2，DO=4，BO=2.5，则CO=

查看试题解析
16. 如果（m+n）（m+n+5）=6，则m+n= ．

查看试题解析
17. 已知关于 $x$ 的方程 $a x^{2} + b x + 1 = 0$ 的两根为 $x_{1} = 1$ ， $x_{2} = 2$ ，则方程 $a {(x + 1)}^{2} + b (x + 1) + 1 = 0$ 的两根之和为.

查看试题解析
18. 如图，A、B是双曲线 $y = \frac{k}{x} (x > 0)$ 上两点，过点B作 $B C ⊥ y$ 轴，垂足为C，BC交AO于C点 $D .$ 已知 $A D = 3 D O$ ， $△ B O D$ 的面积为5，则k的值为.

查看试题解析

三、解答题

19. 解如下方程
$x^{2} - 4 x + 1 = 0$ （用配方法）

查看试题解析
20.
已知：如图，△ABC∽△ADE ， ∠A=45°，∠C=40°．求：∠ADE的度数．

查看试题解析
21. 一个长方体的体积是100cm³ ，它的长是ycm，宽为5cm，高是xcm.

(1)、写出用高表示长的函数关系式；

(2)、写出自变量x的取值范围.

查看试题解析
22. 解下列方程

(1)、2x²-x=0

(2)、x²-4x=4

查看试题解析
23. 如图，在平面直角坐标系中，网格中每个小正方形的边长为1，已知△ABC

（ 1 ）将△ABC绕点O顺时针旋转90画出旋转后得到的△A₁B₁C₁；

（ 2 ）画出△ABC以坐标原点O为位似中心的位似图形△A₂B₂C₂ ，使△A₂B₂C₂在第二象限，与△ABC的位似比是 $\frac{1}{2}$ .

查看试题解析
24. 如图，在 $Δ A B C$ 中，点 $D$ 在边 $A B$ 上， $∠ A C D = ∠ A B C$ ， $A D = 1 ， A B = 3$ .求 $A C$ 的长.

查看试题解析
25. 已知关于x的一元二次方程x²+（2m+3）x+m²=0有两根α，β.

(1)、求m的取值范围；

(2)、若 $\frac{1}{α} + \frac{1}{β} = - 1$ ，则m的值为多少？

查看试题解析
26. 如图，在正方形ABCD中，边长为4，∠MDN＝90°，将∠MDN绕点D旋转，其中DM边分别与射线BA、直线AC交于E、Q两点，DN边与射线BC交于点F；连接EF，且EF与直线AC交于点P.

(1)、如图1，点E在线段AB上时，①求证：AE＝CF；②求证：DP垂直平分EF；

(2)、当AE＝1时，求PQ的长.

查看试题解析