云南省昆明市西山区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式，化简后能与 $\sqrt{2}$ 合并的是（）

A、 $\sqrt{12}$ B、 $\sqrt{24}$ C、 $\sqrt{\frac{1}{8}}$ D、 $\sqrt{4}$

查看试题解析
2. 2021年7月1日是中国共产党成立100周年纪念日，为了让全校学生树立爱国爱党的崇高信念，昆明市某学校开展了形式多样的党史学习教育活动．其中八年级举行了场党史知识竞赛，在决赛中10名学生得分情况如下表

分数

80

85

90

95

人数

1

3

4

2

那么这10名学生所得分数的平均数是（）分

A、88 B、88.5 C、90 D、无法确定

查看试题解析
3. 在△ABC中，∠A、∠B、∠C所对的边分别是a、b、c，下列条件中不能判断△ABC是直角三角形的是（）

A、∠A＝∠B﹣∠C B、a²+b²＝c² C、a＝3，b＝4，c＝5 D、a：b：c＝4：5：6

查看试题解析
4. 某天小明骑自行车上学，途中因自行车发生故障，修车耽误了一段时间后继续骑行，按时赶到了学校.如图描述了他上学的情景，下列说法中错误的是（）

A、自行车发生故障时离家距离为1000米 B、学校离家的距离为2000米 C、到达学校时共用时间20分钟 D、修车时间为15分钟

查看试题解析
5. 如图，两把完全一样的直尺叠放在一起，重合的部分构成一个四边形，这个四边形一定是（）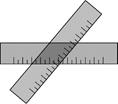

A、矩形 B、菱形 C、正方形 D、无法判断

查看试题解析
6. 如图，O是矩形ABCD的对角线AC的中点，M是AD的中点，若AB＝5，AD＝12，则OM+OB的长为（）

A、7 B、8 C、9 D、10

查看试题解析
7. 一次函数y＝ax+b与正比例函数y＝abx（a、b为常数且ab≠0）在同一平面直角坐标系中的图可能是（）

A、 B、 C、 D、

查看试题解析
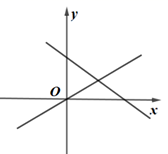8. 如图，矩形ABOC的边BO、CO分别在x轴、y轴上，点A的坐标是（﹣12，8），点D、E分别为AC、OC的中点，点P为OB上一动点，当PD+PE最小时，点P的坐标为（）

A、（﹣1，0） B、（﹣2，0） C、（﹣3，0） D、（﹣4，0）

查看试题解析

二、填空题

9. 函数 $y = \sqrt{x - 1}$ 中自变量x的取值范围是.

查看试题解析
10. “绿水青山就是金山银山”为了响应党中央对环境保护的号召，某校要从报名的甲、乙、丙三人中选取一人去参加昆明市举办的环保演讲比赛经过两轮初赛后，甲、乙丙三人的平均成绩都是89，方差分别是s_甲²＝12，S_乙²＝3.3，S_丙²＝1.5．你认为参加决赛比较合适．

查看试题解析
11. 要使函数y＝2xⁿ^﹣1+3是一次函数，则n的值为．

查看试题解析
12. 如图，菱形ABCD的边长为5，对角线BD的长为8，点E，F分别是边AD，CD的中点，连接EF并延长与BC的延长线相交于点G，则EG的长为．

查看试题解析
13. 如图，直线y＝x+2与直线y＝kx+6交于点P（3，n），则方程组 ${\begin{array}{l} y = x + 2 \\ y = k x + 6 \end{array}$ 的解．

查看试题解析
14. 如图，矩形 $A B C D$ 中， $A B = 6 ， B C = 8$ ，点E是 $B C$ 边上一点，连接 $A E$ ，把 $△ A B E$ 沿 $A E$ 折叠，使点B落在点F处，当 $△ C E F$ 为直角三角形时， $C F$ 的长为.

查看试题解析

三、解答题

15. 计算：

(1)、3 $\sqrt{3} - \sqrt{8} + \sqrt{2} - \sqrt{27}$

(2)、 ${(\sqrt{2} + \sqrt{6})}^{2} - (\sqrt{5} - \sqrt{3}) (\sqrt{5} + \sqrt{3})$

查看试题解析
16. 如图，E、F分别是矩形ABCD的边BC、AD上的点，且BE＝DF．求证：四边形AECF是平行四边形．

查看试题解析
17. 如图，直线y＝kx+b（k≠0）与x轴交于点A（6，0），与y轴交于点B（0，3）与直线y＝x交于点C．

(1)、求k，b的值和点C坐标；

(2)、求△BOC的面积；

(3)、直接写出不等式kx+b≥x的解．

查看试题解析
18. 2021年由我国自主研发的新冠疫苗终于上市，目前我国上市的新冠疫苗分为三种，分别是灭活疫苗、腺病毒载体疫苗、重组亚单位疫苗为了让学生了解更多的疫苗知识，昆明市某中学举行了一次“新冠疫苗知识竞赛”，为了了解本次竞赛情况从中抽取了初一、初二两个年级各50名学生，对他们此次竞赛的成绩（得分取正整数，满分为100分）分别进行了整理、描述和分析．下面给出部分信息
a．初一年级学生竞赛成绩的频数分布直方图如图

（数据分成6组：40≤x＜50，50≤x＜60，60≤x＜70，70≤x＜80，80≤x＜90，90≤x＜100）：

b．初一年级学生竞赛成绩在80≤x＜90这一组的是：

80 81 81 82 82 84 86 86 86 88 88 89

c．这两个年级学生竞赛成绩的平均数、众数、中位数如下：

成绩

平均数

中位数

众数

初一年级学生

82

m

86

初二年级学生

83

85

84

根据以上信息，回答下列问题

(1)、写出表中m的值；

(2)、在此次竞赛中，那个年级竞赛成绩更好？说出你的理由；

(3)、已知该校初一年级有学生400人，估计该校初一年级学生竞赛成绩超过85的人数．

查看试题解析
19. 如图，在4×3正方形网格中，每个小正方形的边长都是1，正方形顶点叫格点，连接两个网格格点的线段叫网格线段，点A固定在格点上．

(1)、若a是图中能用网格线段表示的最小无理数，b是图中能用网格线段表示的最大无理数，则a＝， b＝；

(2)、请你画出顶点在格点上且边长为 $\sqrt{5}$ 的所有菱形ABCD，你画出的菱形面积为；

查看试题解析
20. 阅读材料，回答问题：
观察下列各式

$\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} =$ 1 $+ \frac{1}{1} - \frac{1}{2} =$ 1 $\frac{1}{2}$ ；

$\sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} = 1 + \frac{1}{2} - \frac{1}{3} = 1 \frac{1}{6}$ ；

$\sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} = 1 + \frac{1}{3} - \frac{1}{4} = 1 \frac{1}{12}$ ．

请你根据以上三个等式提供的信息解答下列问题：

(1)、猜想： $\sqrt{1 + \frac{1}{7^{2}} + \frac{1}{8^{2}}} =$ ＝；

(2)、归纳：根据你的观察、猜想，写出一个用n（n为正整数）表示的等式：；

(3)、应用：用上述规律计算 $\sqrt{1 + \frac{1}{1^{2}} + \frac{1}{2^{2}}} + \sqrt{1 + \frac{1}{2^{2}} + \frac{1}{3^{2}}} + \sqrt{1 + \frac{1}{3^{2}} + \frac{1}{4^{2}}} + ... + \sqrt{1 + \frac{1}{9^{2}} + \frac{1}{10^{2}}}$ ．

查看试题解析
21. 如图，在四边形ABCD中，BD为对角线，AD∥BC，BC $= \frac{1}{2}$ AD，∠ABD＝90°，E为AD的中点，连接BE．

(1)、求证：四边形BCDE为菱形；

(2)、连接AC，若AC平分∠BAD，BC＝1，求菱形BCDE的面积．

查看试题解析
22. 某经销商计划用不超过25000元的资金购进A、B两种商品共100件，从市场得知如下信息

A

B

进价（元/件）

500

100

售价（元/件）

650

150

设该经销商购进A商品x件，这两种商品全部销售完后获得利润为y元

(1)、求y与x之间的函数关系式；

(2)、若要求全部销售完后获得的利润不少于8500元，该经销商有哪几种进货方案？

(3)、选择哪种进货方案，该经销商可获利最大？最大利润是多少元？

查看试题解析
23. 如图，在平面直角坐标系中，四边形ABCO是矩形，已知点B坐标为（10，8），M，N分别是OC，AB的中点．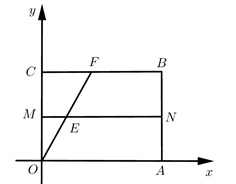

(1)、求证：四边形BCMN是矩形；

(2)、点F是直线BC上一点，连接OF交直线MN于点E，当OF＝OA时，求直线AF的解析式；

(3)、在（2）的条件下，直线l经过点A，且解析式为y＝kx+b（k≠0），若直线l与线段EM相交，求k的取值范围．

查看试题解析

成绩	平均数	中位数	众数
初一年级学生	82	m	86
初二年级学生	83	85	84

分数	80	85	90	95
人数	1	3	4	2

	A	B
进价（元/件）	500	100
售价（元/件）	650	150