山西省吕梁市交城县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 下列各组数中,不是勾股数的是( )A、4,5,6 B、8,15,17 C、6,8,10 D、5,12,132. 下列运算中,正确的是( )A、 B、 C、 D、3. 某小组长统计组内5人一天在课堂上的发言次数分别为3,3,0,4,5.关于这组数据,下列说法错误的是( )A、众数是3 B、中位数是0 C、平均数3 D、方差是2.84. 如图,在△ABC中,三边a、b、c的大小关系是( )
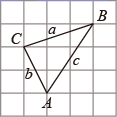 A、a<b<c B、c<a<b C、c<b<a D、b<a<c5. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB′=60°,则矩形ABCD的面积是( )
A、a<b<c B、c<a<b C、c<b<a D、b<a<c5. 如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB′=60°,则矩形ABCD的面积是( ) A、12 B、24 C、12 D、166. 直线 是 关于 的一次函数,则下列说法正确的是( )A、直线与 轴交于点 B、直线不经过第四象限 C、直线与 轴交于点 D、 随 的增大而增大7. 一次函数 与 的图像交于点 ,则 ( )A、 B、 C、 D、8. 如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( )
A、12 B、24 C、12 D、166. 直线 是 关于 的一次函数,则下列说法正确的是( )A、直线与 轴交于点 B、直线不经过第四象限 C、直线与 轴交于点 D、 随 的增大而增大7. 一次函数 与 的图像交于点 ,则 ( )A、 B、 C、 D、8. 如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短距离是( ) A、5 B、25 C、10 +5 D、359. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( )
A、5 B、25 C、10 +5 D、359. 如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB,添加一个条件,不能使四边形DBCE成为矩形的是( ) A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE10. 如图,点P是边长为2cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设P点运动的路程为xcm,则 POD的面积y(cm2)随x(cm)变化的关系图象为( )
A、AB=BE B、BE⊥DC C、∠ADB=90° D、CE⊥DE10. 如图,点P是边长为2cm的正方形ABCD的边上一动点,O是对角线的交点,当点P由A→D→C运动时,设P点运动的路程为xcm,则 POD的面积y(cm2)随x(cm)变化的关系图象为( )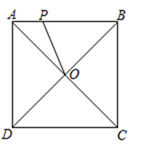 A、
A、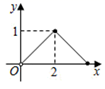 B、
B、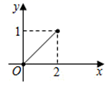 C、
C、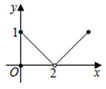 D、
D、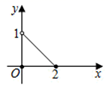
二、填空题
-
11. 如图,已知两正方形的面积分别是25和169,则字母B所代表的正方形的边长是。
 12. 如图,直线y=x+2与直线y=ax+c相交于点P(m , 3),则关于x的不等式x+2≤ax+c的解为 .
12. 如图,直线y=x+2与直线y=ax+c相交于点P(m , 3),则关于x的不等式x+2≤ax+c的解为 .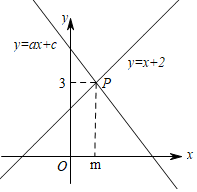 13. 如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是 .
13. 如图,平行四边形ABCD的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长是 . 14. 如图,点 为正方形 外一点, 与 相交于点 .若 ,则 .
14. 如图,点 为正方形 外一点, 与 相交于点 .若 ,则 . 15. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .
15. 如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处,当△CEB′为直角三角形时,BE的长为 .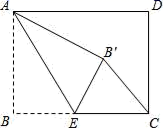
三、解答题
-
16. 计算题:(1)、(2)、17. 如图,四边形ABCD中,AB=3,BC=4,CD=13,AD=12,∠B=90°,求四边形ABCD的面积.
 18. 先观察下列各等式及其验证过程,然后解答问题:
18. 先观察下列各等式及其验证过程,然后解答问题:① 验证: ;
② 验证: ;
解答下列问题:
(1)、按上述两个等式及其验证过程的基本思路,猜想 的变形结果并进行验证;(2)、针对上述各式所反映的一般规律,写出用 为自然数,且 表示的等式,并给出证明.19. 如图,是某型号新能源纯电动汽车充满电后,蓄电池剩余电量 (千瓦时)关于已行驶路程 (千米)的函数图象.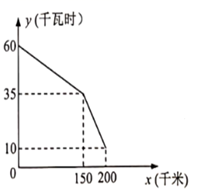 (1)、根据函数图象,蓄电池剩余电量为35千瓦时汽车已经行驶的路程为千米.当 时,消耗1千瓦时的电量,汽车能行驶的路程为千米.(2)、当 时,求 关于 的函数表达式,并计算当汽车已行驶160千米时,蓄电池的剩余电量.20. 如图,在矩形 中, 垂直平分 ,分别交 于点 ,连接 .
(1)、根据函数图象,蓄电池剩余电量为35千瓦时汽车已经行驶的路程为千米.当 时,消耗1千瓦时的电量,汽车能行驶的路程为千米.(2)、当 时,求 关于 的函数表达式,并计算当汽车已行驶160千米时,蓄电池的剩余电量.20. 如图,在矩形 中, 垂直平分 ,分别交 于点 ,连接 . (1)、求证:四边形 是菱形;(2)、若 ,求 的长.21. 我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.
(1)、求证:四边形 是菱形;(2)、若 ,求 的长.21. 我市某中学举办“网络安全知识答题竞赛”,初、高中部根据初赛成绩各选出5名选手组成初中代表队和高中代表队参加学校决赛,两个队各选出的5名选手的决赛成绩如图所示.平均分(分)
中位数(分)
众数(分)
方差(分2)
初中部
a
85
b
高中部
85
c
100
160
 (1)、根据图示计算出a、b、c的值;(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)、计算初中代表队决赛成绩的方差 ,并判断哪一个代表队选手成绩较为稳定.22. 如图,▱ABCD的对角线AC、BD相交于点O,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连结PO并延长交BC于点Q.设点P的运动时间为t秒.
(1)、根据图示计算出a、b、c的值;(2)、结合两队成绩的平均数和中位数进行分析,哪个队的决赛成绩较好?(3)、计算初中代表队决赛成绩的方差 ,并判断哪一个代表队选手成绩较为稳定.22. 如图,▱ABCD的对角线AC、BD相交于点O,AB⊥AC,AB=3,BC=5,点P从点A出发,沿AD以每秒1个单位的速度向终点D运动.连结PO并延长交BC于点Q.设点P的运动时间为t秒. (1)、求BQ的长,(用含t的代数式表示)(2)、当四边形ABQP是平行四边形时,求t的值(3)、当点O在线段AP的垂直平分线上时,直接写出t的值.23. 在平面直角坐标系之中,点O为坐标原点,直线 分别交x、y轴于点B、A,直线 与直线 交于点C.
(1)、求BQ的长,(用含t的代数式表示)(2)、当四边形ABQP是平行四边形时,求t的值(3)、当点O在线段AP的垂直平分线上时,直接写出t的值.23. 在平面直角坐标系之中,点O为坐标原点,直线 分别交x、y轴于点B、A,直线 与直线 交于点C.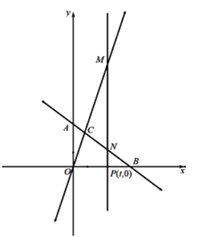
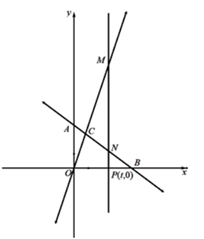
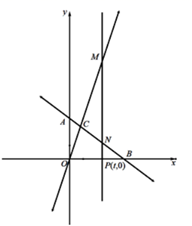
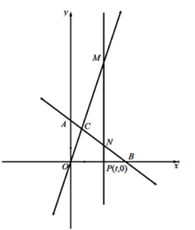 (1)、如图1,求点C的坐标.(2)、如图2,点P(t,0)为C点的右侧x轴上一点,过点P作x轴垂线分别交AB、OC于点N、M,若MN=5NP,求t的值.(3)、如图3,点F为平面内任意一点,是否存在y轴正半轴上一点E,使点E、F、M、N围成的四边形为菱形,若存在求出点E坐标;若不存在,请说明理由.
(1)、如图1,求点C的坐标.(2)、如图2,点P(t,0)为C点的右侧x轴上一点,过点P作x轴垂线分别交AB、OC于点N、M,若MN=5NP,求t的值.(3)、如图3,点F为平面内任意一点,是否存在y轴正半轴上一点E,使点E、F、M、N围成的四边形为菱形,若存在求出点E坐标;若不存在,请说明理由.