山东省烟台市福山区2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 函数y= 的自变量x的取值范围是( )A、x≠5 B、x>3且x≠5 C、x≥3 D、x≥3且x≠52. 下列计算正确的是( )A、 =±4 B、﹣ =﹣8 C、 =2 D、﹣3. 已知反比例函数 的图象上有两点A(x1 , y1)、B(x2 , y2),且x1<x2 , 那么下列结论正确的是( )A、y1<y2 B、y1>y2 C、y1=y2 D、不能确定4. 如图,三角板在灯光照射下形成投影,三角板与其投影的相似比为2:5,且三角板的一边长为8cm,则投影三角板的对应边长为( )
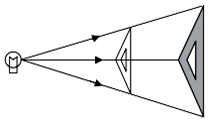 A、20cm B、10cm C、8cm D、3.2cm5. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )
A、20cm B、10cm C、8cm D、3.2cm5. 如图,为估算某河的宽度,在河对岸边选定一个目标点A,在近岸取点B,C,D,使得AB⊥BC,CD⊥BC,点E在BC上,并且点A,E,D在同一条直线上。若测得BE=20m,EC=10m,CD=20m,则河的宽度AB等于( )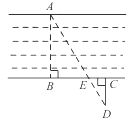 A、60m B、40m C、30m D、20m6. 对于任意实数k,关于x的方程 的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法判定7. 等腰三角形的一边长是3,另两边的长是关于 的方程 的两个根,则 的值为( )A、3 B、4 C、3或4 D、78. 《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.书中有一题“今有户高多于广六尺八寸,两隅相去适一丈,问户高,广各几何?”其大意是:“已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?”若设宽为x尺,则可列方程为( )A、x2+(x﹣6.8)2=100 B、x(x+6.8)=100 C、x2+(x+6.8)2=100 D、x(x﹣6.8)2=1009. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
A、60m B、40m C、30m D、20m6. 对于任意实数k,关于x的方程 的根的情况为( )A、有两个相等的实数根 B、没有实数根 C、有两个不相等的实数根 D、无法判定7. 等腰三角形的一边长是3,另两边的长是关于 的方程 的两个根,则 的值为( )A、3 B、4 C、3或4 D、78. 《九章算术》是中国传统数学重要的著作之一,奠定了中国传统数学的基本框架.书中有一题“今有户高多于广六尺八寸,两隅相去适一丈,问户高,广各几何?”其大意是:“已知长方形门的高比宽多6尺8寸,门的对角线长1丈,那么门的高和宽各是多少?”若设宽为x尺,则可列方程为( )A、x2+(x﹣6.8)2=100 B、x(x+6.8)=100 C、x2+(x+6.8)2=100 D、x(x﹣6.8)2=1009. 生活中到处可见黄金分割的美,如图,在设计人体雕像时,使雕像的腰部以下a与全身 的高度比值接近0.618,可以增加视觉美感,若图中 为2米,则a约为( )
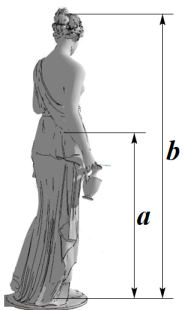 A、1.24米 B、1.38米 C、1.42米 D、1.62米10. 如图,已知在▱ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是( )
A、1.24米 B、1.38米 C、1.42米 D、1.62米10. 如图,已知在▱ABCD中,E为AD的中点,CE的延长线交BA的延长线于点F,则下列选项中的结论错误的是( ) A、FA:FB=1:2 B、AE:BC=1:2 C、BE:CF=1:2 D、S△ABE:S△FBC=1:411. 如图,点A在双曲线 上,点B在双曲线 上,且AB//x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为( )
A、FA:FB=1:2 B、AE:BC=1:2 C、BE:CF=1:2 D、S△ABE:S△FBC=1:411. 如图,点A在双曲线 上,点B在双曲线 上,且AB//x轴,点C、D在x轴上,若四边形ABCD为矩形,则它的面积为( )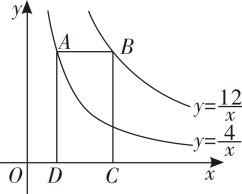 A、4 B、6 C、8 D、1212. 如图,在矩形 中, 点 在 边上, 和 交于点 若 ,则图中阴影部分的面积为( )
A、4 B、6 C、8 D、1212. 如图,在矩形 中, 点 在 边上, 和 交于点 若 ,则图中阴影部分的面积为( )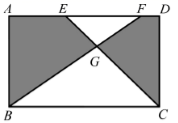 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 若 ,则 .14. 如图,直线l1∥l2∥l3 , 直线AC和DF被l1 , l2 , l3所截,AB=5,BC=6,EF=4,则DE的长为 .
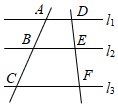 15. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2 , 则修建的路宽应为米.
15. 如图,在一块长15m、宽10m的矩形空地上,修建两条同样宽的相互垂直的道路,剩余分栽种花草,要使绿化面积为126m2 , 则修建的路宽应为米.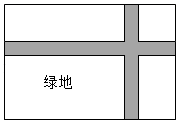 16. 如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=12,则DH= .
16. 如图,在△ABC中,D、E为边AB的三等分点,EF∥DG∥AC,H为AF与DG的交点.若AC=12,则DH= . 17. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 的值为 .
17. 如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且 ,则 的值为 . 18. 如图,已知一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(3,a),点B(14﹣2a,2).若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,则△ACD的面积 .
18. 如图,已知一次函数y=kx+b的图象与反比例函数y= 的图象交于点A(3,a),点B(14﹣2a,2).若一次函数图象与y轴交于点C,点D为点C关于原点O的对称点,则△ACD的面积 .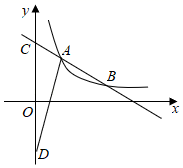
三、解答题
-
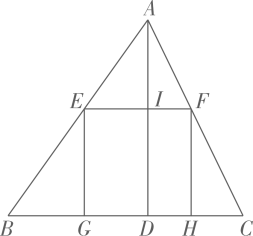
19. 计算:(1)、 ;(2)、 .(3)、用两种不同的方法解方程:x2+4x﹣5=0.20. 已知关于x的一元二次方程 .(1)、求证:无论k为何实数,方程总有两个不相等的实数根;(2)、若方程的两个实数根 , 满足 ,求k的值.21. 如图,△ABC是一块锐角三角形的材料,边BC=120mm , 高AD=80mm , 要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,这个正方形零件的边长是多少mm .
 22. 如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图:
22. 如图所示的平面直角坐标系中,△ABC的三个顶点坐标分别为A(﹣3,2),B(﹣1,3),C(﹣1,1),请按如下要求画图: (1)、以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1 , 请画出△A1B1C1:并写出点B的对应点B1的坐标;(2)、以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2 , 使它与△ABC的位似比为2:1.并写出点B的对应点B2的坐标.(3)、△ABC内部一点M的坐标为(a,b),写出M在△A2B2C2中的对应点M2的坐标.23. 如图,反比例函数 的函数与y=2x的图象相交于点C,过直线上一点A(a,8)作AAB⊥y轴交于点B,交反比函数图象于点D,且AB=4BD.
(1)、以坐标原点O为旋转中心,将△ABC顺时针旋转90°,得到△A1B1C1 , 请画出△A1B1C1:并写出点B的对应点B1的坐标;(2)、以坐标原点O为位似中心,在x轴下方,画出△ABC的位似图形△A2B2C2 , 使它与△ABC的位似比为2:1.并写出点B的对应点B2的坐标.(3)、△ABC内部一点M的坐标为(a,b),写出M在△A2B2C2中的对应点M2的坐标.23. 如图,反比例函数 的函数与y=2x的图象相交于点C,过直线上一点A(a,8)作AAB⊥y轴交于点B,交反比函数图象于点D,且AB=4BD.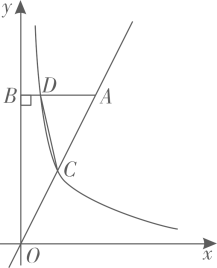 (1)、求反比例函数的解析式;(2)、求四边形OCDB的面积.24. 如图,已如平行四边形 中,点 为坐标顶点,点 ,函数 的图象经过点 .
(1)、求反比例函数的解析式;(2)、求四边形OCDB的面积.24. 如图,已如平行四边形 中,点 为坐标顶点,点 ,函数 的图象经过点 .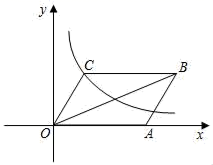 (1)、求 的值及直线 的函数表达式:(2)、求四边形 的周长.25. 如图,在矩形ABCD中,AB=20,点E是BC边上的一点,将△ABE沿着AE折叠,点B刚好落在CD边上点G处;点F在DG上,将△ADF沿着AF折叠,点D刚好落在AG上点H处,此时S△GFH:S△AFH=2:3.
(1)、求 的值及直线 的函数表达式:(2)、求四边形 的周长.25. 如图,在矩形ABCD中,AB=20,点E是BC边上的一点,将△ABE沿着AE折叠,点B刚好落在CD边上点G处;点F在DG上,将△ADF沿着AF折叠,点D刚好落在AG上点H处,此时S△GFH:S△AFH=2:3. (1)、求证:△EGC∽△GFH;(2)、求AD的长;(3)、求HF的值.26. 在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.
(1)、求证:△EGC∽△GFH;(2)、求AD的长;(3)、求HF的值.26. 在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点.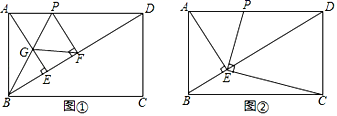 (1)、若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;(2)、若PE⊥EC,如图②,求证:AE•AB=DE•AP;(3)、在(2)的条件下,若AB=1,BC=2,求AP的长.
(1)、若BP平分∠ABD,交AE于点G,PF⊥BD于点F,如图①,证明四边形AGFP是菱形;(2)、若PE⊥EC,如图②,求证:AE•AB=DE•AP;(3)、在(2)的条件下,若AB=1,BC=2,求AP的长.