山东省临沂市沂水县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 要使二次根式 有意义,实数x的取值范围是( )A、x≥2021 B、x>2021 C、x≠2021 D、x≤20212. 一次函数 的图象大致是( )A、
 B、
B、 C、
C、 D、
D、 3. 在下列各式中,化简正确的是( )A、 3 B、 a2 C、 D、4. 某校足球队有17名队员,队员的年龄情况统计如表:
3. 在下列各式中,化简正确的是( )A、 3 B、 a2 C、 D、4. 某校足球队有17名队员,队员的年龄情况统计如表:年龄 岁
13
14
15
16
人数
3
5
6
3
则这17名队员年龄的中位数和众数分别是( )
A、14,15 B、15,15 C、14.5,14 D、14.5,155. 一组数据1,2,1,4的方差为( )A、1 B、1.5 C、2 D、2.56. 关于一次函数 ,下列说法中正确的是( )A、y随x的增大而增大 B、图象经过第一、二、三象限 C、与x轴交于 D、与y轴交于7. 如图,在平行四边形ABCD中,点O是对角线AC,BD的交点,AC⊥BC,且AB=5,AD=3,则OA的长是( ) A、 B、2 C、2 D、48. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、
A、 B、2 C、2 D、48. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )A、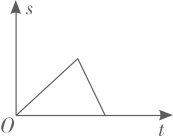 B、
B、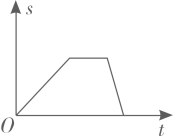 C、
C、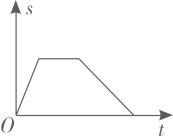 D、
D、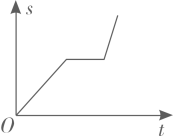 9. 已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形10. 对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图根据图中信息,这些学生的平均分( )
9. 已知M、N是线段AB上的两点,AM=MN=2,NB=1,以点A为圆心,AN长为半径画弧;再以点B为圆心,BM长为半径画弧,两弧交于点C,连接AC,BC,则△ABC一定是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等腰三角形10. 对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分4个等级,将调查结果绘制成如下条形统计图和扇形统计图根据图中信息,这些学生的平均分( ) A、2.5 B、2.95 C、3 D、3.2511. 赵爽弦图是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).若小正方形和大正方形的面积分别是1和5,则直角三角形两条直角边长分别为( )
A、2.5 B、2.95 C、3 D、3.2511. 赵爽弦图是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).若小正方形和大正方形的面积分别是1和5,则直角三角形两条直角边长分别为( ) A、2,1 B、1, C、2, D、2,12. 某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:
A、2,1 B、1, C、2, D、2,12. 某学习小组利用同一块木板,测量了小车从不同高度下滑的时间,他们得到如表数据:支撑物的高度
10
20
30
40
50
60
70
80
小车下滑的时间
4.23
3.00
2.45
2.13
1.89
1.71
1.59
1.50
下列说法错误的是( )
A、当h=60cm时,t=1.71s B、随着h逐渐升高,t逐渐变小 C、h每增加10cm,t减小1.23s D、随着h逐渐升高,小车下滑的平均速度逐渐加快13. 如图所示,在菱形ABCD中,AC,BD相交于O,∠ABC=50°,E是线段AO上一点则∠BEC的度数可能是( ) A、95° B、75° C、55° D、35°14. 一次函数y1=kx+b与y2=mx+n的图象如图所示,则以下结论:①y1随x的增大而增大;②m>0:③n>0;④不等式mx+n≥kx+b的解集是x≤2.正确的个数是( )
A、95° B、75° C、55° D、35°14. 一次函数y1=kx+b与y2=mx+n的图象如图所示,则以下结论:①y1随x的增大而增大;②m>0:③n>0;④不等式mx+n≥kx+b的解集是x≤2.正确的个数是( ) A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
15. 某校为了选拔一名百米赛跑运动员参加市中学生运动会,组织了 次预选赛,其中甲,乙两名运动员较为突出,他们在 次预选赛中的成绩(单位:秒)如下表所示:
甲
乙
由于甲,乙两名运动员的成绩的平均数相同,学校决定依据他们成绩的稳定性进行选拔,那么被选中的运动员是 .
16. 如图,点G为正方形ABCD内一点,AB=AG,∠AGB=70°,联结DG,那么∠GAC= . 17. 将直线y=2x+2向左平移2个单位长度,所得直线的解析式为 .18. 《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面尺高.
17. 将直线y=2x+2向左平移2个单位长度,所得直线的解析式为 .18. 《九章算术》是中国传统数学的重要著作之一,奠定了中国传统数学的基本框架.如图所示是其中记载的一道“折竹”问题:“今有竹高一丈,末折抵地,去根三尺,问折者高几何?”题意是:一根竹子原高1丈(1丈 10尺),中部有一处折断,竹梢触地面处离竹根3尺,试问折断处离地面多高?答:折断处离地面尺高. 19. 如图,王阿姨在超市购买某种水果所付款金额y(元)与购买量x(千克)之间的函数图象如图所示,则一次购买6千克这种水果比平均分3次购买可节省 元.
19. 如图,王阿姨在超市购买某种水果所付款金额y(元)与购买量x(千克)之间的函数图象如图所示,则一次购买6千克这种水果比平均分3次购买可节省 元.
三、解答题
-
20. 计算:(1)、 2(2)、( 1)2﹣( 1)221. 某校举办了一次成语知识竞赛,满分10分,学生得分均为整数,成绩达到6分及6分以上为合格,达到9分或10分为优秀,这次竞赛中,甲、乙两组学生成绩分布的折线统计图和成绩统计分析表如下所示.
 (1)、求出下列成绩统计分析表中a,b的值:
(1)、求出下列成绩统计分析表中a,b的值: (2)、小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.22. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.
(2)、小英同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上面表格判断,小英是甲、乙哪个组的学生;(3)、甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你写出两条支持乙组同学观点的理由.22. 在△ABC中,AB=15,BC=14,AC=13,求△ABC的面积.某学习小组经过合作交流,给出了下面的解题思路,请你按照他们的解题思路完成解答过程.

 23. 已知,如图,一次函数的图象经过了点P(3,2)和B(0,﹣2),与x轴交于点A.
23. 已知,如图,一次函数的图象经过了点P(3,2)和B(0,﹣2),与x轴交于点A.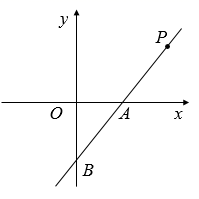 (1)、求一次函数的解析式;(2)、点M在y轴上,且 ABM的面积为 ,求点M的坐标.24. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .
(1)、求一次函数的解析式;(2)、点M在y轴上,且 ABM的面积为 ,求点M的坐标.24. 如图,在矩形ABCD中,O为对角线AC的中点,过点O作直线分别与矩形的边AD , BC交于M , N两点,连接CM , AN .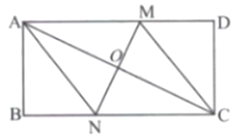 (1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.25. 已知函数y=|x|﹣2
(1)、求证:四边形ANCM为平行四边形;(2)、若AD=4,AB=2,且MN⊥AC , 求DM的长.25. 已知函数y=|x|﹣2 (1)、画出该函数的图象;
(1)、画出该函数的图象;列表:
x
…
…
y
…
…
描点,连线得到函数图象:
(2)、写出该函数的两条性质;(3)、点P(x1 , y1),Q(x2 , y2)在该函数的图象上,若x1+x2=0,求证:y1﹣y2=0.26. 甲、乙两车分别从A,B两地同时出发相向而行,6小时相遇.在行驶过程中乙车因故障停止行驶,排除故障后,乙车提高了速度且保持不变,继续行驶.甲车在行驶过程中速度保持不变.甲、乙两车的路程和y(km)与甲车行驶时间x(h)之间的函数关系如图所示 (1)、A,B两地的路程 , 甲车的速度是 , 乙车排除故障后的速度是;(2)、当3≤x≤6时,求y与x之间的函数解析式;(3)、在整个过程中,甲行驶多长时间时,甲与乙的路程相等?
(1)、A,B两地的路程 , 甲车的速度是 , 乙车排除故障后的速度是;(2)、当3≤x≤6时,求y与x之间的函数解析式;(3)、在整个过程中,甲行驶多长时间时,甲与乙的路程相等?