山东省济宁市泗水县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 二次根式 的x的取值范围是( )A、 B、 C、 D、2. 已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )A、k>5 B、k<5 C、k>−5 D、k<−53. 下列根式中,最简二次根式是( )A、 B、 C、 D、4. 一次函数 与 的图象如图所示,则 的解集是( )
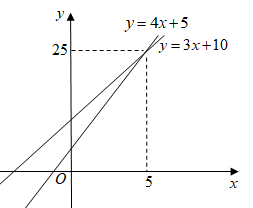 A、 B、 C、 D、5. 如图,点 表示的实数是( )
A、 B、 C、 D、5. 如图,点 表示的实数是( )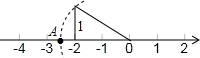 A、 B、 C、 D、6. 小明同学对数据26,36,36,46,5■,52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、方差 C、中位数 D、众数7. 若一次函数 的图象经过点P(1,-1),则该函数图象必经过点( )A、 B、 C、 D、8. 下列图象中,可以表示一次函数 与正比例函数 (k,b为常数,且kb≠0)的图象的是( )A、
A、 B、 C、 D、6. 小明同学对数据26,36,36,46,5■,52进行统计分析.发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、方差 C、中位数 D、众数7. 若一次函数 的图象经过点P(1,-1),则该函数图象必经过点( )A、 B、 C、 D、8. 下列图象中,可以表示一次函数 与正比例函数 (k,b为常数,且kb≠0)的图象的是( )A、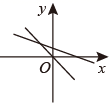 B、
B、 C、
C、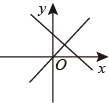 D、
D、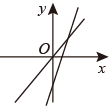 9. 如图,四边形 是菱形, , , 于 ,则 等于( )
9. 如图,四边形 是菱形, , , 于 ,则 等于( ) A、 B、 C、4 D、510. 某移动通讯公司提供了A,B两种方案的通讯费用y(元)与通话时间x(分)之间的关系,如图所示,则以下说法错误的是( )
A、 B、 C、4 D、510. 某移动通讯公司提供了A,B两种方案的通讯费用y(元)与通话时间x(分)之间的关系,如图所示,则以下说法错误的是( )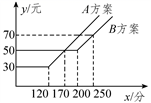 A、若通话时间少于120分,则A方案比B方案便宜20元 B、若通话时间超过200分,则B方案比A方案便宜12元 C、若通讯费用为60元,则B方案比A方案的通话时间多 D、若两种方案通讯费用相差10元,则通话时间是145分或185分11. 如图,在正方形 中,点 的坐标是 ,则 点的坐标是( )
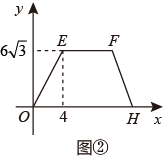
A、若通话时间少于120分,则A方案比B方案便宜20元 B、若通话时间超过200分,则B方案比A方案便宜12元 C、若通讯费用为60元,则B方案比A方案的通话时间多 D、若两种方案通讯费用相差10元,则通话时间是145分或185分11. 如图,在正方形 中,点 的坐标是 ,则 点的坐标是( )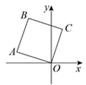 A、 B、 C、 D、12. 如图①,在 ABCD中,∠B=120°,动点P从点B出发,沿B→C→D→A运动至点A停止,如图②是点P运动时,△PAB的面积 随点P运动的路程x(cm)变化的关系图象,则图②中H点的横坐标为( )
A、 B、 C、 D、12. 如图①,在 ABCD中,∠B=120°,动点P从点B出发,沿B→C→D→A运动至点A停止,如图②是点P运动时,△PAB的面积 随点P运动的路程x(cm)变化的关系图象,则图②中H点的横坐标为( )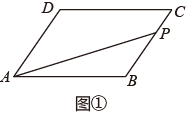
 A、12 B、14 C、16 D、
A、12 B、14 C、16 D、二、填空题
-
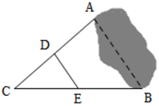
13. 已知一组数据10,8,9,x,5的众数是8,那么这组数据的方差是14. 已知 是正比例函数,且y随x的减小而减小,则m= .15. 如图,要测量池塘两岸相对的A , B两点间的距离,可以在池塘外选一点C , 连接AC , BC , 分别取AC , BC的中点D , E , 测得DE=50m , 则AB的长是m .
 16. 某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为分.17. 在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .18. 如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形AC C1D1 , 使∠D1AC=60°;连接AC1 , 再以A C1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;……按此规律所作的第n个菱形的边长为 .
16. 某校拟招聘一批优秀教师,其中某位教师笔试、试讲、面试三轮测试得分分别为92分、85分、90分,综合成绩笔试占40%,试讲占40%,面试占20%,则该名教师的综合成绩为分.17. 在 ABCD中,AE平分∠BAD交边BC于点E,DF平分∠ADC交边BC于点F,若AD=11,EF=5,则AB= .18. 如图,边长为1的菱形ABCD中,∠DAB=60°.连接对角线AC,以AC为边作第二个菱形AC C1D1 , 使∠D1AC=60°;连接AC1 , 再以A C1为边作第三个菱形AC1C2D2 , 使∠D2AC1=60°;……按此规律所作的第n个菱形的边长为 .
三、解答题
-
19.(1)、 ;(2)、 .20. 在正方形ABCD中,P是对角线AC上的点,连接BP、DP.
 (1)、求证:BP=DP;(2)、如果AB=AP,求∠ABP的度数.21. 在寻找某坠毁飞机的过程中,两艘搜救艇接到消息,在海面上有疑似漂浮目标A、B.于是,一艘搜救艇以16海里/时的速度离开港口O(如图)沿北偏东40°的方向向目标A前进,同时,另一艘搜救艇也从港口O出发,以12海里/时的速度向着目标B出发,1.5小时后,他们同时分别到达目标A、B.此时,他们相距30海里,请问第二艘搜救艇的航行方向是北偏西多少度?
(1)、求证:BP=DP;(2)、如果AB=AP,求∠ABP的度数.21. 在寻找某坠毁飞机的过程中,两艘搜救艇接到消息,在海面上有疑似漂浮目标A、B.于是,一艘搜救艇以16海里/时的速度离开港口O(如图)沿北偏东40°的方向向目标A前进,同时,另一艘搜救艇也从港口O出发,以12海里/时的速度向着目标B出发,1.5小时后,他们同时分别到达目标A、B.此时,他们相距30海里,请问第二艘搜救艇的航行方向是北偏西多少度?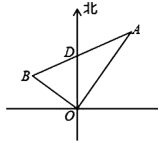 22. 为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:
22. 为弘扬传统文化,某校开展了“传承经典文化,阅读经典名著”活动.为了解七、八年级学生(七、八年级各有600名学生)的阅读效果,该校举行了经典文化知识竞赛.现从两个年级各随机抽取20名学生的竞赛成绩(百分制)进行分析,过程如下:收集数据:
七年级:79,85,73,80,75,76,87,70,75,94,75,79,81,71,75,80,86,59,83,77.
八年级:92,74,87,82,72,81,94,83,77,83,80,81,71,81,72,77,82,80,70,41.
整理数据:
七年级
0
1
0
a
7
1
八年级
1
0
0
7
b
2
分析数据:
平均数
众数
中位数
七年级
78
75
八年级
78
80.5
应用数据:
(1)、由上表填空:a= , b= , c= , d=.(2)、估计该校七、八两个年级学生在本次竞赛中成绩在90分以上的共有多少人?(3)、你认为哪个年级的学生对经典文化知识掌握的总体水平较好,请说明理由.23. 在函数中,我们把关于x的一次函数y=ax+b与y=bx+a称为一对交换函数,如y=3x+1与y=x+3是一对交换函数.称函数y=3x+1与是函数y=x+3的交换函数.(1)、求函数 与交换函数的图象的交点坐标;(2)、若函数 (b为常数)与交换函数的图象及纵轴所围三角形的面积为4,求b的值.24. 某校校园超市老板到批发中心选购甲、乙两种品牌的文具盒,乙品牌的进货单价是甲品牌进货单价的2倍,考虑各种因素,预计购进乙品牌文具盒的数量y(个)与甲品牌文具盒的数量x(个)之间的函数关系如图所示.当购进的甲、乙品牌的文具盒中,甲有120个时,购进甲、乙品牌文具盒共需7200元.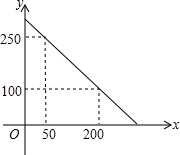 (1)、根据图象,求y与x之间的函数关系式;(2)、求甲、乙两种品牌的文具盒进货单价;(3)、若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?25. 如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为 ,折痕为CE,已知 .
(1)、根据图象,求y与x之间的函数关系式;(2)、求甲、乙两种品牌的文具盒进货单价;(3)、若该超市每销售1个甲种品牌的文具盒可获利4元,每销售1个乙种品牌的文具盒可获利9元,根据学生需求,超市老板决定,准备用不超过6300元购进甲、乙两种品牌的文具盒,且这两种品牌的文具盒全部售出后获利不低于1795元,问该超市有几种进货方案?哪种方案能使获利最大?最大获利为多少元?25. 如图,在直角坐标系中放入一个矩形纸片ABCO,BC=10,将纸片翻折后,点B恰好落在x轴上,记为 ,折痕为CE,已知 . (1)、求点 的坐标;(2)、求折痕CE所在直线的解析式;(3)、若点P是y轴上的一个动点,当△CPE为等腰三角形时,请求出点P的坐标.
(1)、求点 的坐标;(2)、求折痕CE所在直线的解析式;(3)、若点P是y轴上的一个动点,当△CPE为等腰三角形时,请求出点P的坐标.