青海省海东市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、填空题

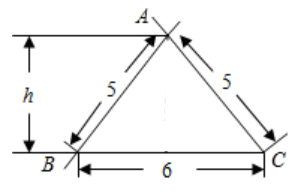
1. 若二次根式 $\sqrt{x + 1}$ 有意义，则x的取值范围是．

查看试题解析
2. 计算： $\sqrt{4 \times 9} =$ ； $(3 + 2 \sqrt{2}) (3 - 2 \sqrt{2}) =$ ．

查看试题解析
3. 跳高训练时，甲、乙两名同学在相同条件下各跳了10次，统计他们的平均成绩都是1.36米，且方差为 $s^{2}_{甲} =0 .4$ ， $s^{2}_{乙} = 0.3$ ，则成绩较为稳定的是（填“甲”或“乙”）．

查看试题解析
4. 直角三角形两直角边长分别为5cm和12cm，则斜边上的中线长为cm．

查看试题解析
5. 已知 $M (- 2 ， y_{1})$ ， $N (3 ， y_{2})$ 是直线 $y = 3 x + 1$ 上的两个点，则 $y_{1}$ 、 $y_{2}$ 的大小关系是（填“>”“=”或“<”）．

查看试题解析
6. 已知一个三角形工件尺寸（单位： $dm$ ）如图所示，则高h是 $dm$ ，它的面积是 ${dm}^{2}$ ．

查看试题解析
7. 已知直线y＝x+b和y＝ax﹣3交于点P（2，1），则关于x的方程x+b＝ax﹣3的解为．

查看试题解析
8. 如图，点D和点E分别是 $B C$ 和 $B A$ 的中点，已 $A C = 4$ ，则 $D E =$ ．

查看试题解析
9. 面试时，某人的基础知识、表达能力、工作态度的得分分别是80分、70分、90分，若依次按照30%、30%、40%的比例确定面试成绩，则这个人的面试成绩是分.

查看试题解析
10. 如图，已知正比例函数 $y_{1} = k x$ 与上次函数及 $y_{2} = - x + b$ 的图象交于点P．下面有四个结论：① $k > 0$ ；② $b > 0$ ；③当 $x > 0$ 时， $y_{1} > 0$ ；④当 $x < - 2$ 时， $k x > - x + b$ ．其中正确的是．（填序号）

查看试题解析
11. 如图，在矩形ABCD中，M、N分别是边 $A D$ 、 $B C$ 的中点，E、F分别是线段 $B M$ 、 $C M$ 的中点．若 $A B = 8$ ， $A D = 12$ ，则四边形 $E N F M$ 的周长为，面积为．

查看试题解析
12. 如图，正方形ABCD的边长为 $\sqrt{2}$ ，O是对角线BD上一动点（点O与端点B，D不重合），OM⊥AD于点M，ON⊥AB于点N，连接MN，则MN长的最小值为．

查看试题解析

二、单选题

13. 下列各组数中能作为直角三角形的三边长的是（　　）

A、1，2，3 B、3，4，5 C、4，5，6 D、7，8，9

查看试题解析
14. 下列各式中，运算正确的是（）

A、 $\sqrt{12} =2 \sqrt{3}$ B、 $3 \sqrt{3} - \sqrt{3} = 3$ C、2+ $\sqrt{3}$ ＝2 $\sqrt{3}$ D、 $\sqrt{{(- 2)}^{2}} = - 2$

查看试题解析
15. 将直线 $y = 3 x$ 沿 $y$ 轴向下平移1个单位长度后得到的直线解析式为（）

A、 $y = 3 x + 1$ B、 $y = 3 x - 1$ C、 $y = x + 1$ D、 $y = x - 1$

查看试题解析
16. 今年库尔勒某一周七天每一天最高气温变化如折线图所示，则关于这组数据的描述正确的是（）

A、最小值是32 B、众数是33 C、中位数是34 D、平均数是34

查看试题解析
17. 如图，在菱形ABCD中，对角线BD＝4，AC＝3BD，则菱形ABCD的面积为（　　）

A、96 B、48 C、24 D、6

查看试题解析
18. 若正比例函数y＝（m﹣2）x的图象经过点A(x₁ ， y₁)和点B(x₂ ， y₂)，当x₁＜x₂时，y₁＞y₂ ，则m的取值范围是（　　）

A、m＞0 B、m＜0 C、m＞2 D、m＜2

查看试题解析
19. 如图，矩形ABCD中，AC，BD交于点O，M，N分别为BC，OC的中点．若MN＝3，CD＝6，则∠ACB的度数为（）

A、30° B、35° C、45° D、60°

查看试题解析
20. 已知 $a$ 、 $b$ 、 $c$ 是三角形的三边长，如果满足 ${(a - 6)}^{2} + \sqrt{b - 8} + | c - 10 | = 0$ ，则三角形的形状是（）

A、底与腰不相等的等腰三角形 B、等边三角形 C、钝角三角形 D、直角三角形

查看试题解析

三、解答题

21. 计算： $\sqrt{6} \times \sqrt{2} + \sqrt{6} \div \sqrt{2} - \sqrt{27}$ ．

查看试题解析
22. 如图所示，在△ABC中，AB＝5，AC＝13，BC边上的中线AD＝6，求BC的长．

查看试题解析
23. 如图，直线l₁：y＝x＋1与直线l₂：y＝mx＋n相交于点P（1，b）．

(1)、求b的值；

(2)、不解关于x，y的方程组 ${\begin{array}{l} y = x + 1 \\ y = m x + n \end{array}$ ，请你直接写出它的解；

(3)、直线l₃：y＝nx＋m是否也经过点P？请说明理由．

(4)、直接写出不等式x+1≥mx+n的解集．

查看试题解析
24. 暑假期间，小刚一家乘车去离家380公里的某景区旅游，他们离家的距离 $y (km)$ 与汽车行驶时间 $x (h)$ 之间的三段函数图象如图所示．

(1)、三段图象中，汽车行驶的速度最慢的是哪段？为多少？

(2)、求线段 $A B$ 对应的函数表达式；

(3)、小刚一家出发2.5小时时，离目的地还有多少 $km$ ？

查看试题解析

25. 某校八年级举行了“学习防护知识，预防新型冠状病毒肺炎”的知识竞赛活动．为了解全年级600名学生此次竞赛成绩：（百分制）的情况，随机抽取了部分参赛学生的成绩，整理并绘制出如图不完整的统计表和扇形统计图；根据相关信息，解答下列问题：

组别	分数/分	人数/人
A	$60 \leq x < 70$	a
B	$70 \leq x < 80$	12
C	$80 \leq x < 90$	18
D	$90 \leq x < 100$	24

(1)、本次接受随机抽样调查的学生人数为人；统计表a=；

(2)、抽取的参赛学生的成绩的中位数所在的组别是；

(3)、请你估计，该校八年级竞赛成绩达到80分以上（含80分）的学生约有多少人？

查看试题解析

26. 如图，在平行四边形ABCD中，点E是边AD的中点，连接CE并延长交BA的延长线于点F，连接AC，DF．

(1)、求证： $△$ AEF≌ $△$ DEC；

(2)、求证：四边形ACDF是平行四边形．

查看试题解析
27. 已知：P是正方形 $A B C D$ 对角线 $B D$ 上一点， $P E ⊥ D C$ ， $P E ⊥ B C$ ，垂足分别为E、F．

(1)、求证： $A P = C P$ ；

(2)、若 $∠ D A P = 30 °$ ， $P D = \sqrt{2}$ ，求 $C P$ 的长．

查看试题解析
28. 今年，“地摊经济”成为了社会关注的热门话题．小明从市场得知如下信息：

甲商品

乙商品

进价（元/件）

35

5

售价（元/件）

45

8

小明计划购进甲、乙商品共100件进行销售．设小明购进甲商品x件，甲、乙商品全部销售完后获得利润为y元．

(1)、求出y与x之间的函数关系式；

(2)、小明用不超过2000元资金一次性购进甲，乙两种商品，求x的取值范围；

(3)、在（2）的条件下，若要求甲，乙商品全部销售完后获得的利润不少于632.5元，请说明小明有哪些可行的进货方案，并计算哪种进货方案的利润最大．

查看试题解析

	甲商品	乙商品
进价（元/件）	35	5
售价（元/件）	45	8