辽宁省大连市庄河市2020-2021学年八年级下学期数学期末试卷
试卷更新日期：2021-09-02 类型：期末考试
一、单选题
-
1. 使式子 成立的x的取值范围是（ ）A、x≥2 B、x＞2 C、x＜2 D、x≤22. 某跳远队准备选取一批队员参加比赛，要比较谁的成绩稳定，应选用的统计量是（ ）A、平均数 B、众数 C、中位数 D、方差3. 下列算式计算正确的是（ ）A、 B、 C、 D、2 24. 下列各组数中不能作为直角三角形的三边长是（ ）A、5，12，14 B、1.5，2，2.5 C、 ，3，4 D、6，8，105. 菱形具有而平行四边形不一定具有的性质是（ ）A、对角线互相平分 B、对角线相等 C、对角线互相垂直 D、对边平行且相等6. 下列图象中，不能表示y是x的函数的是（ ）A、
B、
C、
D、
7. 一家鞋店在一段时间内销售某种女鞋的情况如下表：尺码/cm
22
22.5
23
23.5
24
24.5
25
销售量/双
2
3
6
14
13
7
2
则此组数据的众数是（ ）
A、22 B、23 C、23.5 D、248. 某水果批发市场规定，批发苹果重量不少于100kg时，批发价为2.5元/kg，批发苹果重量多于100kg时，超过的部分按批发价打八折．若某人批发苹果重量为x（x＞100）kg时，需支付多少现金，可列式子为（ ）A、100x B、100x+2.5×0.8×（x﹣100） C、100×2.5+2.5×0.8×（x﹣100） D、x+2.5×（x﹣100）9. 如图1，在矩形ABCD中，动点E从点A出发，沿A→B→C→D方向运动至点D停止，设点E的运动路程为x，△ADE的面积为y，如果y关于x的函数图象如图2所示，则矩形ABCD的面积是（ ）
A、18 B、12 C、9 D、310. 下列说法：①一次函数y x+2的图象从左向右下降，y随x的增大而减小；②函数y=2x与y=﹣x+3的交点在第三象限；
③若正比例函数y=kx经过点（﹣1，3），则k ．
其中正确的是（ ）
A、① B、② C、①③ D、①②③二、填空题
-
11. 化简： = ．12. 在一次空气污染指数抽查中，收集到7天的数据如下：56，71，66，59，68，78，80．则该组数据的中位数是 ．13. 2021年6月17日，中国第七艘载人航天飞船“神舟十二号”圆满发射成功，这将意味着中国的载人航天飞船脱离试验阶段，实现太空长期驻守和太空往返常态化．现有甲、乙两名航天员要进行飞行前的考核，按照2：3：3：2的比例确定成绩，甲、乙两人成绩（百分制）如表：
候选人
心理素质
身体素质
科学头脑
应变能力
甲
86
85
88
90
乙
90
82
80
90
最后应选 ．
14. 如图，在矩形ABCD中，对角线AC、BD交于点O，点E是CD中点，且∠COD=60°．如果AB=2，那么矩形ABCD的面积是 ．
15. 实数a、b在数轴上的位置如图所示，则化简 的结果是 ．
16. 如图，在矩形ABCD中，E是AD中点，将△ABE沿BE翻折，使点A的对应点G落在矩形ABCD的内部，BG的延长线与CD相交于点F，且F恰好是CD中点，若AB=2，则AD= ．
三、解答题
-
17. 计算： ．18. 函数 与 的图象如图所示．
(1)、求k的值；(2)、观察图象直接写出kx＞3﹣2x的x的取值范围．19. 如图，在▱ABCD中，点K为AD中点，连接BK交CD的延长线于点E，连接AE、BD．求证：四边形ABDE为平行四边形．
20. 某学校为了解本校学生体育锻炼情况，随机抽查了部分学生一周参加体育锻炼时间，并将调查结果进行统计，下面是根据调查结果绘制的两幅统计图（均不完整）．
(1)、本次共抽查学生多少人？(2)、请将统计图1补充完整；(3)、若该校共有800名学生，请估计该校每周锻炼时间在7小时及以上的学生人数．21. 如图，某工厂制作一个三角形工件，若∠A=45°，∠B=60°，BC=6．求AC的长．
22. 如图，在矩形ABCD中，连接对角线AC，分别过点B、点D作AC的垂线交于点E、F．证明：AF=CE．
23. 如图，在平面直角坐标系xOy中，OA=OB，∠AOB=90°，过点B作x轴的平行线，与过A点的直线y=﹣x+b交于点C，且点A的坐标为（2，1）．
(1)、求点C和点D的坐标；(2)、求∠ACB的度数．24. 甲、乙两人沿同一路线从学校出发到图书馆，甲先步行出发，6分钟后乙骑自行车出发，乙比甲先到图书馆，甲、乙两人在此过程中以各自的速度匀速运动．甲、乙两人离学校的距离y（米）与甲的行走时间x（分）之间的函数图象如图1所示，甲、乙两人间的距离S（米）与甲的行走时间x（分）之间的函数图象如图2所示．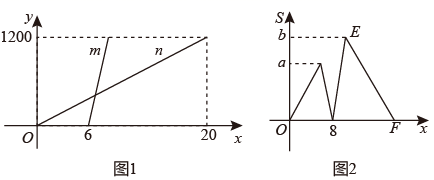
(1)、图1中甲运动的图象是 ， 乙运动的图象是 ；（填m、n）(2)、甲的速度为米/分，乙的速度为米/分；(3)、图2中，a= ，b= ；(4)、图2中，求线段EF所在直线的函数解析式．25. 如图，在平面直角坐标系中，点A坐标为（0，3），点C坐标为（6，0），AB x轴，且OA=AB，动点P从点O出发以2个单位/秒的速度沿O→A→B→C的路线匀速运动，运动到点C时终止．过点P作PQ⊥x轴，垂足为Q，设点P的运动时间为x（s），线段PQ的长为y．
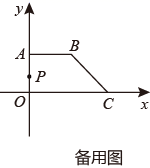(1)、求∠C的度数；(2)、求y与x的函数关系式．26. 阅读下列材料：数学课上老师出示了这样一个问题：如图，正方形ABCD中，点E、H在BC边上，连接AE、DH交于点F，且AF=AD，过点F作FG⊥FD交AB于点G，若AG=4，EF=2，求EC的长．
某学习小组的同学经过思考，交流了自己的想法：
小强：“通过观察和度量，发现∠BGF与∠DHC存在某种数量关系”；
小诺：“解决几何试题的关键在于找到几何模型（如图基本模型）”；
小新：“通过构造三角形，证明三角形全等，进而可以得到线段AG和HC之间的数量关系，进而可以求出EC长．”
⋯⋯
参考以上思考问题的方法或用其它方法解答下列问题：
(1)、猜想∠BGF与∠DHC的数量关系，并证明；(2)、探究线段AG和HC之间的数量关系，并证明；(3)、直接写出线段EC长．