吉林省四平市伊通满族自治县2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{x - 1} + \sqrt{x - 3}$ 中，x的取值范围是（）

A、x≥3 B、x≥1 C、1≤x≤3 D、不能确定

查看试题解析
2. 如图，数轴上点A，B表示的数分别是1，2，过点B作PQ⊥AB，以点B为圆心，AB长为半径画弧，交PQ于点C，以原点O为圆心，OC长为半径画弧，交数轴于点M，则点M表示的数是（）

A、 $\sqrt{3}$ B、 $\sqrt{5}$ C、 $\sqrt{6}$ D、 $\sqrt{7}$

查看试题解析
3. 某校七年级有13名同学参加百米竞赛，预赛成绩各不相同，要取前6名参加决赛，小梅已经知道了自己的成绩，她想知道自己能否进入决赛，还需要知道这13名同学成绩的（）

A、中位数 B、众数 C、平均数 D、极差

查看试题解析
4. 如图，直线 $y = k x + b$ 交坐标轴于 $A$ ， $B$ 两点，则关于 $x$ 的不等式 $k x + b < 0$ 的解集是 $($ $)$

A、 $x > - 2$ B、 $x > 3$ C、 $x < - 2$ D、 $x < 2$

查看试题解析
5. 四边形ABCD中，对角线AC、BD相交于点O，下列条件不能判定这个四边形是平行四边形的是（）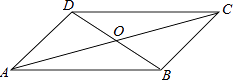

A、AB∥DC，AD∥BC B、AB=DC，AD=BC C、AO=CO，BO=DO D、AB∥DC，AD=BC

查看试题解析
6. 小明的父亲饭后出去散步，从家中出发走20分钟到一个离家900米的报亭看报10分钟后，用15分钟返回家，下列图中表示小明的父亲离家的距离y（米）与离家的时间x（分）之间的函数关系的是（）

A、 B、 C、 D、

查看试题解析

二、填空题

7. 比较大小： $2 \sqrt{3}$ $3 \sqrt{2}$ （填“＞”、“＜”或“＝”）.

查看试题解析
8. 已知：Rt△ABC中，∠C＝90°，AC＝3，BC＝4，P为AB上任意一点，PF⊥AC于F，PE⊥BC于E，则EF的最小值是．

查看试题解析
9. 如图所示，菱形ABCD的对角线AC＝16cm，BD＝12cm，则菱形ABCD的周长为 cm．

查看试题解析
10. 如图所示，在▱ABCD中，AC与BD相交于点O，点E是BC边的中点，BC＝5cm，OE＝1.5cm，▱ABCD的周长＝cm．

查看试题解析
11. 将直线y＝2x+3向下平移2个单位，得直线．

查看试题解析
12. 如图，在直角三角形ABC中，∠ACB＝90°，AC＝ $\sqrt{13}$ ，点E、F分别为AC和AB的中点，若EF＝ $\sqrt{3}$ ，则CF＝．

查看试题解析
13. 如图，在菱形ABCD中，点A在x轴上，点B的坐标为（4，1），点D的坐标为（0，1），则点C的坐标为．

查看试题解析
14. 当b的取值范围是时，直线y＝3x﹣b与直线y＝2x+1的交点在第二象限．

查看试题解析

三、解答题

15. 计算：9 $\sqrt{3}$ +7 $\sqrt{12}$ ﹣5 $\sqrt{8}$ × $\sqrt{6}$ ．

查看试题解析
16. 先化简，再求值： $(6 x \sqrt{\frac{y}{x}} + \frac{3}{y} \sqrt{x y^{3}})$ － $(4 y \sqrt{\frac{x}{y}} + \sqrt{36 x y})$ ，其中x＝ $\sqrt{2}$ ＋1，y＝ $\sqrt{2}$ －1.

查看试题解析
17.
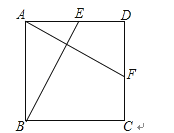
如图，正方形ABCD中，点E，F分别在AD，CD上，且AE=DF，连接BE，AF．求证：BE=AF．

查看试题解析
18. 如图，已知直线y＝kx+b经过点A、点B．求此直线与x轴的交点C的坐标．

查看试题解析
19. 2013年我省松原地震后，某中学开展了“我为灾区献爱心”捐款活动，八年级一班的团支部对全班50人捐款数额进行了统计，并绘制了下面统计图．

(1)、把统计图补充完整；

(2)、直接写出这组数据的众数和中位数；

(3)、该校共有学生1600人，请你根据八年级一班的捐款情况，估计该中学的捐款总数．

查看试题解析
20. 如图，四边形ABCD是菱形，AE⊥BC，AF⊥CD，分别交CB、CD的延长线于点E、点F．

(1)、求证：△ABE≌△ADF；

(2)、若CD＝5，AE＝3，则四边形AECF的面积为．

查看试题解析
21. 甲、乙两名自行车运动员在同一条公路上进行骑自行车训练，他们同时同地同向出发，乙在行驶途中变过一次速度，甲、乙两人各自在公路上训练时行驶路程y（千米）与行驶时间x（小时）（0≤x≤4）之间的函数图象如图所示．

(1)、甲行驶的速度为；

(2)、求乙改变速度后行驶路程y（千米）与行驶时间x（小时）之间的函数解析式；

(3)、当甲、乙相距5千米时，x对应的值为．

查看试题解析
22. 如图，在△ABC中，AB＝AC，D为边BC上一点，以AB、BD为邻边作▱ABDE，连接AD、EC，AC和DE相交于点O．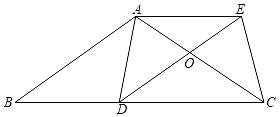

(1)、求证：OD＝OC；

(2)、若BD＝CD，求证：四边形ADCE是矩形．

查看试题解析
23. 类比平行四边形，我们学习筝形定义：两组临边分别相等的四边形叫做筝形，如图①，若AD＝CD，AB＝CB，则四边形ABCD是筝形．

(1)、在同一平面内，△ABC与△ADE按如图②所示放置，其中∠B＝∠D＝90°，AB＝AD，BC与DE相交于点F．请你判断四边形ABFD是不是筝形，说明理由；

(2)、请你结合图形①，写出一个筝形的判断方法；（定义除外）

(3)、如图③，△OGH为等边三角形，点G的坐标为（ $\sqrt{3}$ ﹣1，0），点P为直线y＝﹣x上的一点．在第四象限内是否存在点P，使得以O、G、H、P为顶点的四边形为筝形？若存在，请直接写出点P的坐标；若不存在，请说明理由．

查看试题解析
24. 如图，正方形ABCD的边长为2cm，动点P从B点出发沿B﹣C﹣D的方向运动到点D停止，在此运动过程中，设△ADP的面积为y（cm²），点P运动的路程为x（cm）．

(1)、x的值为时，△ADP为等腰三角形；

(2)、当点P在BC边上时，y＝；

(3)、当点P在CD边上时（点P不与D点重合），求y与x之间的函数解析式，并在平面直角坐标系中，直接画出此函数的图象；

(4)、求当△ADP的面积等于正方形ABCD面积的 $\frac{1}{3}$ 时，x的值是多少？

查看试题解析