黑龙江省绥化市绥棱县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 下列二次根式中,属于最简二次根式的是( )A、 B、 C、 D、2. 下列各图给出了变量x与y之间的函数是( )A、
 B、
B、 C、
C、 D、
D、 3. 下列计算结果正确的是( )A、 B、 C、 D、4. 矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )A、12 B、10 C、7.5 D、55. 正方形具备而菱形不具备的性质是( )A、四条边都相等 B、四个角都是直角 C、对角线互相垂直平分 D、每条对角线平分一组对角6. 在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )A、a=9,b=41,c=40 B、a=5,b=12,c=13 C、a:b:c=3:4:5 D、a=11,b=12,c=157. 关于函数y=﹣x﹣2的图象,有如下说法:
3. 下列计算结果正确的是( )A、 B、 C、 D、4. 矩形的两条对角线的夹角为60度,对角线长为15,则矩形的较短边长为( )A、12 B、10 C、7.5 D、55. 正方形具备而菱形不具备的性质是( )A、四条边都相等 B、四个角都是直角 C、对角线互相垂直平分 D、每条对角线平分一组对角6. 在下列以线段a,b,c的长为三边的三角形中,不能构成直角三角形的是( )A、a=9,b=41,c=40 B、a=5,b=12,c=13 C、a:b:c=3:4:5 D、a=11,b=12,c=157. 关于函数y=﹣x﹣2的图象,有如下说法:①图象过点(0,2);
②图象与x轴的交点是(2,0);
③由图象可知y随x的增大而增大;
④图象不经过第一象限;
⑤图象是与y=﹣x+2平行的直线.
其中正确的说法有( )
A、5个 B、4个 C、3个 D、2个8. 如图,已知四边形ABCD是平行四边形,下列结论中错误的是()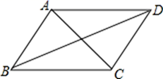 A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形9. 一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )A、
A、当AB=BC时,它是菱形 B、当AC⊥BD时,它是菱形 C、当∠ABC=90°时,它是矩形 D、当AC=BD时,它是正方形9. 一次函数y=mx+n与y=mnx(mn≠0),在同一平面直角坐标系的图象是( )A、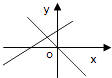 B、
B、 C、
C、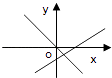 D、
D、 10. 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
10. 如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF .
其中,将正确结论的序号全部选对的是( )
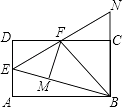 A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
11. 若式子 在实数范围内有意义,则x的取值范围是 .12. 若函数y=(k+1)x+k2-1是正比例函数,则k的值为。13. 数据“1,2,1,3,3”,则这组数据的方差是 .
14. 如图,在Rt△ABC中,∠ACB=90°,AC=9,BC=12,则点C到AB的距离CD= .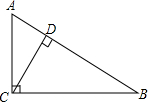 15. 若x,y为实数,且满足|x﹣3|+ =0,则( )2021的值是 .16. 已知直角三角形的两边长分别为3、4.则第三边长为.17. 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .
15. 若x,y为实数,且满足|x﹣3|+ =0,则( )2021的值是 .16. 已知直角三角形的两边长分别为3、4.则第三边长为.17. 已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值= .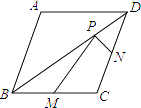 18. 如图,▱ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为cm.
18. 如图,▱ABCD的周长是26cm,对角线AC与BD交于点O,AC⊥AB,点E是BC的中点,△AOD的周长比△AOB的周长多3cm,则AE的长度为cm. 19. 如图,把矩形ABCD沿EF翻转,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是
19. 如图,把矩形ABCD沿EF翻转,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是 20. 在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为
20. 在平面直角坐标系中,直线y=kx+x+1过一定点A,坐标系中有点B(2,0)和点C,要使以A、O、B、C为顶点的四边形为平行四边形,则点C的坐标为三、解答题
-
21. 计算:(1)、(2)、 .22. 当今,青少年视力水平下降已引起全社会的关注,为了了解某市3000名学生的视力情况,从中抽取了一部分学生进行了一次抽样调查,利用所得数据绘制的频数分布直方图如图,解答下列问题:
 (1)、本次抽样调查共抽测了名学生;(2)、参加抽测的学生的视力的众数在范围内;中位数在范围内;(3)、若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?23. 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
(1)、本次抽样调查共抽测了名学生;(2)、参加抽测的学生的视力的众数在范围内;中位数在范围内;(3)、若视力为4.9及以上为正常,试估计该市学生的视力正常的人数约为多少?23. 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0). (1)、请直接写出点B关于点A对称的点的坐标;(2)、将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.24. 先观察下列各等式及其验证过程,然后解答问题:
(1)、请直接写出点B关于点A对称的点的坐标;(2)、将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.24. 先观察下列各等式及其验证过程,然后解答问题:① 验证: ;
② 验证: ;
解答下列问题:
(1)、按上述两个等式及其验证过程的基本思路,猜想 的变形结果并进行验证;(2)、针对上述各式所反映的一般规律,写出用 为自然数,且 表示的等式,并给出证明.25. 甲乙两车分别从A、B两地相向而行,甲车出发1小时后乙车出发,并以各自速度匀速行驶,两车相遇后依然按照原速度原方向各自行驶,如图所示是甲乙两车之间的距离S(千米)与甲车出发时间t(小时)之间的函数图象,其中D点表示甲车到达B地,停止行驶.
 (1)、A、B两地的距离千米;乙车速度是;a表示 .(2)、乙出发多长时间后两车相距330千米?26. 已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E.
(1)、A、B两地的距离千米;乙车速度是;a表示 .(2)、乙出发多长时间后两车相距330千米?26. 已知:如图,平行四边形ABCD中,O是CD的中点,连接AO并延长,交BC的延长线于点E. (1)、求证: ;(2)、连接AC,DE,当 四边形ACED是正方形?请说明理由 .27. 无锡火车货运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物往徐州,这列货车可挂A、B两种不同规格的货厢50节,已知用一节A型货厢的运费是0.5万元,用一节B型货厢的运费是0.8万元.(1)、设运输这批货物的总运费为y (万元),用A型货箱的节数为x (节),试写出y与x之间的函数关系式;(2)、已知甲种货物35吨和乙种货物15吨,可装满一节A型货厢,甲种货物25吨和乙种货物35吨吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,有哪几种运输方案?请你设计出来.(3)、利用函数的性质说明,在这些方案中,哪种方案总运费最少?最少运费是多少万元?28. 如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.
(1)、求证: ;(2)、连接AC,DE,当 四边形ACED是正方形?请说明理由 .27. 无锡火车货运站现有甲种货物1530吨,乙种货物1150吨,安排用一列货车将这批货物往徐州,这列货车可挂A、B两种不同规格的货厢50节,已知用一节A型货厢的运费是0.5万元,用一节B型货厢的运费是0.8万元.(1)、设运输这批货物的总运费为y (万元),用A型货箱的节数为x (节),试写出y与x之间的函数关系式;(2)、已知甲种货物35吨和乙种货物15吨,可装满一节A型货厢,甲种货物25吨和乙种货物35吨吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,有哪几种运输方案?请你设计出来.(3)、利用函数的性质说明,在这些方案中,哪种方案总运费最少?最少运费是多少万元?28. 如图,正方形ABCD中,AC是对角线,今有较大的直角三角板,一边始终经过点B,直角顶点P在射线AC上移动,另一边交DC于Q.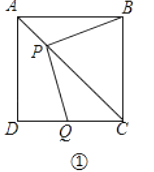
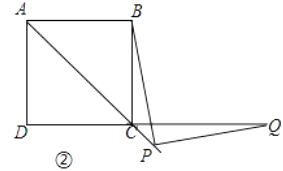 (1)、如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;(2)、如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.
(1)、如图①,当点Q在DC边上时,猜想并写出PB与PQ所满足的数量关系,并加以证明;(2)、如图②,当点Q落在DC的延长线上时,猜想并写出PB与PQ满足的数量关系,并证明你的猜想.