黑龙江省绥化市海伦市2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 二次根式 $\sqrt{a - 2}$ 在实数范围内有意义，则a的取值范围是（）

A、 $a \geq 2$ B、 $a > 2$ C、 $0 < a < 2$ D、 $a < 2$

查看试题解析
2. 下列计算正确的是（）

A、 $2 \sqrt{3} + 3 \sqrt{2} = 5 \sqrt{3}$ B、 $\sqrt{8} \div \sqrt{2} = 2$ C、 $5 \sqrt{2} \times 5 \sqrt{3} = 5 \sqrt{6}$ D、 $4 \sqrt{3} - \sqrt{3} = 4$

查看试题解析
3. 甲、乙、丙、丁四位选手各射击10次，每人的平均成绩都是9.3环，方差如表：

选手

甲

乙

丙

丁

方差（环²）

0.035

0.016

0.022

0.025

则这四个人种成绩发挥最稳定的是（）

A、甲 B、乙 C、丙 D、丁

查看试题解析
4. 下列各线段的长，能构成直角三角形的是（）

A、9，16，25 B、5，12，13 C、 $\sqrt{5}$ ， $\sqrt{4}$ ， $\sqrt{5}$ D、 $\frac{1}{3}$ ， $\frac{1}{4}$ ， $\frac{1}{5}$

查看试题解析
5. 下列四个命题中，真命题是（　）

A、对角线互相垂直的四边形是菱形 B、对角线互相平分且垂直的四边形是矩形 C、顺次连接矩形四边中点得到的四边形是菱形 D、对角线互相垂直相等的四边形是正方形

查看试题解析
6. 五名女生的体重（单位： $kg$ ）分别为：37、40、38、42、42，这组数据的众数和中位数分别是（）

A、38、40 B、42、38 C、40、42 D、42、40

查看试题解析
7. 如图，点 $A (- 1 ， 2)$ 是一次函数 $y = k x + b (k > 0 ）$ 图象上的一点，则关于x的不等式 $k x + b \geq 2$ 的解集是（）

A、 $0 \leq x \leq 2$ B、 $x \geq 2$ C、 $x \geq - 1$ D、 $x \leq - 1$

查看试题解析
8. 关于一次函数y＝﹣2x+3，下列结论正确的是（）

A、图象过点（1，﹣1） B、图象经过一、二、三象限 C、y随x的增大而增大 D、当x＞ $\frac{3}{2}$ 时，y＜0

查看试题解析
9. 如图，将边长为2的正方形OABC放在平面直角坐标系中，O是原点，点A的横坐标为1，则点C的坐标为（）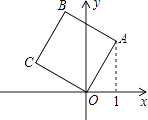

A、（﹣2，1） B、（﹣1，2） C、（ $\sqrt{3}$ ，﹣1） D、（﹣ $\sqrt{3}$ ，1）

查看试题解析
10. 我市某小区实施供暖改造工程，现甲、乙两工程队分别同时开挖两条600米长的管道，所挖管道长度y（米）与挖掘时间x（天）之间的关系如图所示，则下列说法中，正确的个数有（）个．
①甲队每天挖100米；
②乙队开挖两天后，每天挖50米；
③当x=4时，甲、乙两队所挖管道长度相同；
④甲队比乙队提前2天完成任务．

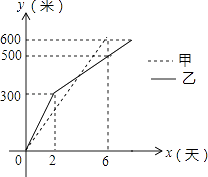A、1 B、2 C、3 D、4

查看试题解析

二、填空题

11. 在函数 $y = \frac{\sqrt{x}}{x - 1}$ 中，自变量x的取值范围是.

查看试题解析
12. 平行四边形ABCD中，∠A－∠B＝20°，则∠A＝， ∠B＝.

查看试题解析
13. 若一组数据 $x_{1}$ ， $x_{2}$ ， $x_{3}$ 的平均数是2，则数据 $x_{1} + 1$ ， $x_{2} + 1$ ， $x_{3} + 1$ 的平均数是．

查看试题解析
14. 将直线y＝﹣4x+3向下平移4个单位，得到的直线解析式是.

查看试题解析
15. 若直线 $y = m x + 1$ 与直线 $y = 2 x - 1$ 的交点在x轴上，则 $m =$ .

查看试题解析
16. 某公司要招聘职员，竟聘者需通过计算机、语言表达和写作能力测试，李丽的三项成绩百分制依次是70分，90分，80分，其中计算机成绩占 $50 %$ ，语言表达成绩占 $30 %$ ，写作能力成绩占 $20 %$ ，则李丽最终的成绩是分.

查看试题解析
17. 实数a、b在数轴上对应点的位置如图所示，化简： $\sqrt{a^{2}} + \sqrt{{(a + b)}^{2}} - | a - b |$ = ．

查看试题解析
18. 已知一次函数y=(1－m)x＋m－2，当m时，y随x的增大而增大．

查看试题解析
19. 等腰 $Δ A B C$ 中， $A B = A C ， B D ⊥ A C$ 于点 $D ， B D = 6 ， A D = 8$ ，则 $C D$ 的长为．

查看试题解析
20. 如图，依次连接第一个矩形各边的中点得到一个菱形，再依次连接菱形各边的中点得到第二个矩形，按照此方法继续下去.已知第一个矩形的面积为1，则第n个矩形的面积为.

查看试题解析

三、解答题

21. 计算：

(1)、 $\sqrt{8} + \sqrt{12} - (\sqrt{27} - \sqrt{\frac{1}{2}})$ ；

(2)、 $(2 \sqrt{48} - 3 \sqrt{27}) \div \sqrt{3}$ ．

查看试题解析

22. 2020年4月是我国第32个爱国卫生月.某校八年级通过网课举行了主题为“防疫有我，爱卫同行”的知识竞赛活动，对全校2200名学生“预防新冠病毒知识”进行了测试（试卷满分100分），从中随机抽取了20名学生的测试卷，按

A ， B ， C ， D ， E

五个级别分别进行了统计，其中得分在C级别这一范围内的成绩分别是：70，72，74，76，77，78，78，78，79，79

（数据整理与描述）将调查结果绘制成如下的统计表和不完整的统计图：

级别	分数	频数	频率
A	$0 \leq x < 60$	2	0.10
B	$60 \leq x < 70$	m	0.20
C	$70 \leq x < 80$	10	0.50
D	$80 \leq x < 90$	3	n
E	$90 \leq x < 100$	1	0.05

（数据应用）请根据以上信息解答下列问题：

(1)、填空：

m =

，

n =

；

(2)、补全频数分布直方图；

(3)、被抽取的20名学生成绩的中位数为；

(4)、若这次测试成绩不低于80分的确定为优秀，请估计该校这次测试获得优秀的学生人数.

查看试题解析

23. 如图，在平行四边形 $A B C D$ 中，点 $O$ 是 $A C$ 与 $B D$ 的交点，过点 $O$ 的直线 $E F$ 与 $A B$ 、 $C D$ 的延长线分别交于点 $E$ 、 $F$ ．

(1)、求证： $△ B O E ≌ △ D O F$

(2)、连接 $C E$ 和 $A F$ ，当 $E F ⊥ A C$ 时，四边形 $A E C F$ 是怎样的特殊四边形？证明你的结论．

查看试题解析
24. 小锤和豆花要测量校园里的一块四边形场地ABCD（如图所示）的周长，其中边BC上有水池及建筑遮挡，没有办法直接测量其长度.小锤经测量得知AB＝AD＝5m，∠A＝60°，DC＝13m，∠ABC＝150°.豆花说根据小锤所得的数据可以求出CB的长度.你同意豆花的说法吗？若同意，请求出CB的长度；若不同意，请说明理由.

查看试题解析
25. 如图，直线y=2x+3与x轴相交于点A，与y轴相交于点B.

(1)、求A，B两点的坐标；

(2)、过B点作直线与x轴交于点P，若△ABP的面积为 $\frac{15}{4}$ ，试求点P的坐标.

查看试题解析
26.
甲、乙两车从A地驶向B地，并以各自的速度匀速行驶，甲车比乙车早行驶2h，并且甲车途中休息了0.5h，如图是甲乙两车行驶的距离y（km）与时间x（h）的函数图象．

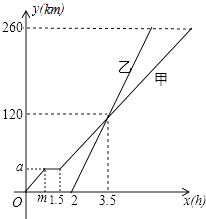(1)、求出图中m，a的值；

(2)、求出甲车行驶路程y（km）与时间x（h）的函数解析式，并写出相应的x的取值范围；

(3)、当乙车行驶多长时间时，两车恰好相距50km．

查看试题解析
27. 在正方形 $A B C D$ 中，连接 $A C$ ，点 $E$ 在线段 $A D$ 上，连接 $B E$ 交 $A C$ 于 $M$ ，过点 $M$ 作 $F M ⊥ B E$ 交 $C D$ 于 $F$ ．

(1)、如图①，求证：∠ABE+∠CMF=∠ACD；

(2)、如图②，求证：BM=MF；

(3)、如图③，连接BF，当AE：AD=1：2，AB=6时，求BF的长．

查看试题解析

选手	甲	乙	丙	丁
方差（环²）	0.035	0.016	0.022	0.025