黑龙江省齐齐哈尔市铁锋区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算中，计算结果正确的是（）

A、 $a^{2} \cdot a^{3} = a^{6}$ B、 $a^{8} \div a^{2} = a^{4}$ C、 ${(a^{2} b)}^{2} = a^{2} b^{2}$ D、 $\sqrt{27} - \sqrt{3} = 2 \sqrt{3}$

查看试题解析
2. 下列各组数是勾股数的一组是（）

A、7，24，25 B、 $\sqrt{3}$ ， $\sqrt{4}$ ， $\sqrt{7}$ C、1.5，2，2.5 D、3² ， 4² ， 5²

查看试题解析
3. 在四边形ABCD中，AD∥BC，下列选项中，不能判定四边形ABCD为矩形的是（）

A、AD＝BC且AC＝BD B、AD＝BC且∠A＝∠B C、AB＝CD且∠A＝∠C D、AB＝CD且∠A＝∠B

查看试题解析
4. 如图，一根竹竿AB，斜靠在竖直的墙上，P是AB中点，A′B′表示竹竿AB端沿墙上、下滑动过程中的某个位置，则在竹竿AB滑动过程中OP（）

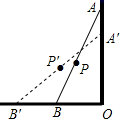A、下滑时，OP增大 B、上升时，OP减小 C、无论怎样滑动，OP不变 D、只要滑动，OP就变化

查看试题解析
5. 如图，A，B两点被池塘隔开，在AB外选一点C，连接AC，BC，并分别找出它们的中点D，E，连接DE，现测得DE=40m，则AB长为（）

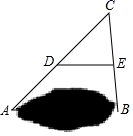A、20m B、40m C、60m D、80m

查看试题解析
6. 多年来，北京市以强有力的措施和力度治理大气污染，空气质量持续改善，主要污染物的年平均浓度值全面下降．下图是1998年至2019年二氧化硫（SO₂）和二氧化氮（NO₂）的年平均浓度值变化趋势图．下列说法错误的是（）

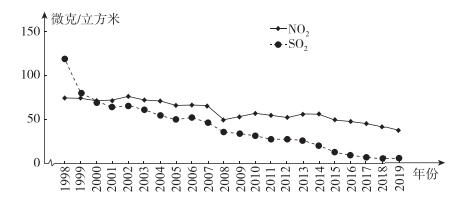A、1998年至2019年，SO₂的年平均浓度值的平均数小于NO₂的年平均浓度值的平均数 B、1998年至2019年，SO₂的年平均浓度值的中位数小于NO₂的年平均浓度值的中位数 C、1998年至2019年，SO₂的年平均浓度值的方差小于NO₂的年平均浓度值的方差 D、1998年至2019年，SO₂的年平均浓度值比NO₂的年平均浓度值下降得更快

查看试题解析
7. 如图所示的是一种数值转换程序，当输入的x值为﹣0.5时，输出的y值为（）

A、﹣2 B、 $\frac{21}{4}$ C、﹣6 D、4

查看试题解析
8. 直线y₁＝k₁x+b与直线y₂＝k₂x在同一平面直角坐标系中的图象如图所示，则关于x的不等式k₁x+b≤k₂x的解为（）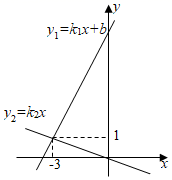

A、x＞﹣3 B、x＜﹣3 C、x≤﹣3 D、x≥﹣3

查看试题解析
9. “赵爽弦图”是由4个全等的直角三角形与中间的一个小正方形拼成的一个大正方形（如图所示）．若直角三角形的两条直角边的长分别是2和1，则图中阴影区域的面积与大正方形的面积之比为（）

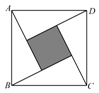A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{1}{5}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
10. 已知正比例函数 $y = k x (k \neq 0)$ 的图象过点 $(2 ， 3)$ ，把正比例函数 $y = k x (k \neq 0)$ 的图象平移，使它过点 $(1 ， - 1)$ ，则平移后的函数图象大致是（）

A、 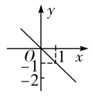B、 C、 D、

查看试题解析

二、填空题

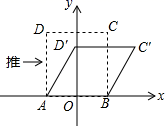
11. 要使函数 $y = \frac{\sqrt{2 x - 1}}{x - 1} + {(x - 3)}^{0}$ 有意义，则x的取值范围是．

查看试题解析
12. 我们知道，四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB的中点是坐标原点O，固定点A，B，把正方形沿箭头方向推，使点D落在y轴正半轴上点D'处，则点C的对应点C'的坐标为．

查看试题解析
13.
在数轴上表示实数a的点如图所示，化简 $\sqrt{{(a - 5)}^{2}}$ ＋|a－2|的结果为．

查看试题解析
14. 在平面直角坐标系xOy中，平行四边形的三个顶点O（0，0），A（3，0），B（3，2），则其第四个顶点C的坐标是．

查看试题解析
15. 在菱形ABCD中，∠A=30°，在同一平面内，以对角线BD为底边作顶角为120°的等腰三角形BDE，则∠EBC的度数为．

查看试题解析
16. 在矩形ABCD中，AB＝6，AD＝5，点P在AD上，连接CP，PB，则PC+PB的最小值为．

查看试题解析
17. 如图，在平面直角坐标系中，等腰直角三角形①沿x轴正半轴滚动并且按一定规律变换，每次变换后得到的图形仍是等腰直角三角形．第一次滚动后点A₁（0，2）变换到点A₂（6，0），得到等腰直角三角形②；第二次滚动后点A₂变换到点A₃（6，0），得到等腰直角三角形③；第三次滚动后点A₃变换到点A₄（10，4 $\sqrt{2}$ ），得到等腰直角三角形④；第四次滚动后点A₄变换到点A₅（10+12 $\sqrt{2}$ ，0），得到等腰直角三角形⑤；依此规律…，则第2020个等腰直角三角形的面积是．

查看试题解析

三、解答题

18. 计算：

(1)、 $(2 \sqrt{12} - 6 \sqrt{\frac{1}{3}} + 3 \sqrt{48}) \div (2 \sqrt{3})$ ；

(2)、 $(2 \sqrt{5} + 5 \sqrt{2}) (2 \sqrt{5} - 5 \sqrt{2}) - {(\sqrt{5} - \sqrt{2})}^{2}$ ．

查看试题解析
19. 阅读下列材料，然后回答问题．在进行二次根式的化简与运算时，我们有时会碰上如 $\frac{5}{\sqrt{3}} ， \sqrt{\frac{2}{3}} ， \frac{2}{\sqrt{3} + 1}$ 一样的式子，其实我们还可以将其进一步化简：
$\frac{5}{\sqrt{3}} = \frac{5 \times \sqrt{3}}{\sqrt{3} \times \sqrt{3}} = \frac{5 \sqrt{3}}{3}$ （一）

$\sqrt{\frac{2}{3}} = \sqrt{\frac{2 \times 3}{3 \times 3}} = \frac{\sqrt{6}}{3}$ （二）

$\frac{2}{\sqrt{3} + 1} = \frac{2 \times (\sqrt{3} - 1)}{(\sqrt{3} + 1) (\sqrt{3} - 1)} = \frac{2 (\sqrt{3} - 1)}{{(\sqrt{3})}^{2} - 1^{2}} = \sqrt{3} - 1$ （三）

以上这种化简的步骤叫做分母有理化．

(1)、请化简： $\frac{2}{\sqrt{3}}$ ＝．

(2)、参照（三）式化简： $\frac{2}{\sqrt{5} + \sqrt{3}}$ ＝．

查看试题解析
20. 如图，在Rt△ABC中，∠ACB＝90°，D ， E分别是边AB ， BC的中点，连接DE并延长到点F ，使EF＝DE ，连接CF ， BF ．

(1)、求证：四边形CFBD是菱形；

(2)、连接AE ，若CF＝ $\sqrt{10}$ ，DF＝2，求AE的长．

查看试题解析
21. 某学校未了解今年九年级学生足球运球的掌握情况，随机抽取部分九年级学生足球运球的测试成绩作为一个样本，按 $A$ ， $B$ ， $C$ ， $D$ 四个等级进行统计，制成了如下不完整的统计图.

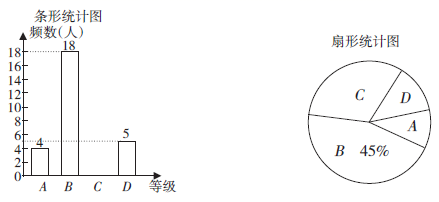
根据所给信息，解答以下问题

(1)、在扇形统计图中， $C$ 对应的扇形的圆心角是度；

(2)、补全条形统计图；

(3)、该校九年级有300名学生，请估计足球运球测试成绩达到 $A$ 级的学生有多少人？

查看试题解析
22. 在一条公路上依次有A，B，C三地，甲车从A地出发，驶向C地，同时乙车从C地出发驶向B地，到达B地停留0.5小时后，按原路原速返回C地，两车匀速行驶，甲车比乙车晚1.5小时到达C地．两车距各自出发地的路程y（千米）与时间x（小时）之间的函数关系如图所示．请结合图象信息解答下列问题：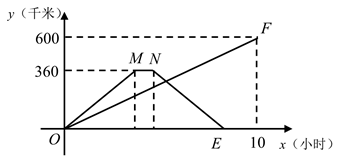

(1)、甲车行驶速度是千米1时，B，C两地的路程为千米；

(2)、求乙车从B地返回C地的过程中，y（千米）与x（小时）之间的函数关系式（不需要写出自变量x的取值范围）；

(3)、出发多少小时，行驶中的两车之间的路程是15千米？请你直接写出答案．

查看试题解析
23. 综合与实践．折纸是我们在研究轴对称问题时最常见的活动．例如教材八年级下册的数学活动﹣﹣折纸，就引起了许多同学的兴趣．在经历图形变换的过程中，进一步发展了同学们的空间观念，积累了数学活动经验．
实践发现：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展平；再一次折叠纸片，使点A落在EF上的点N处，并使折痕经过点B，得到折痕BM，把纸片展平，连接AN，如图1

(1)、折痕直线BM（填“是”或“不是”）线段AN的垂直平分线；请判断图中△ABN是什么特殊三角形？答：；进一步计算出∠MNE＝°；

(2)、继续折叠纸片，使点A落在BC边上的点H处，并使折痕经过点B，得到折痕BG，把纸片展平，如图2，则∠GBN＝°；

(3)、解决问题：
如图3，折叠矩形纸片ABCD，使点A落在BC边上的点A'处，并且折痕交BC边于点T，交AD边于点S，把纸片展平，连接AA'交ST于点O，连接AT．求证：四边形SATA'是菱形．

查看试题解析
24. 综合与探究．如图，在平面直角坐标系xOy中，直线AB与x轴，y轴分别交于点A（3，0）、点B（0，4），点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．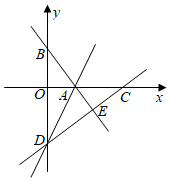

(1)、直接写出AB的长；

(2)、点C的坐标，点D的坐标；

(3)、求直线AB的函数表达式；

(4)、y轴上是否存在一点P，使得S_△PAB＝ $\frac{1}{2}$ S_△OCD？若存在，直接写出点P的坐标；若不存在，请说明理由．

查看试题解析