黑龙江省齐齐哈尔市讷河市等五县市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
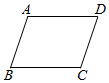
1. 下列计算正确的是( )A、 B、 C、 D、2. 如图,在▱ABCD中,若AB=2,BC= ,则▱ABCD的周长为( )
 A、 B、 C、 D、3. 函数y=﹣2x的图象一定经过下列四个点中的( )A、(﹣2,4) B、(﹣3,﹣6) C、( ,3) D、( ,﹣ )4. 下列各式中最简二次根式为( )A、 B、 C、 D、5. 一组数据由4个数组成,其中3个数分别为4,5,6,且这组数据的平均数为4,则这组数据的中位数为( )A、4.5 B、5.5 C、5 D、46. 将直线y=3x﹣1向上平移2个单位长度,平移后的直线所对应的函数解析式为( )A、y=3x+5 B、y=3x﹣3 C、y=3x+1 D、y=3x+37. 如图,直线y=﹣ 分别交x轴于点A,y轴于点B,点D、E分别是线段AB、AO的中点,连结DE,则DE的长是( )
A、 B、 C、 D、3. 函数y=﹣2x的图象一定经过下列四个点中的( )A、(﹣2,4) B、(﹣3,﹣6) C、( ,3) D、( ,﹣ )4. 下列各式中最简二次根式为( )A、 B、 C、 D、5. 一组数据由4个数组成,其中3个数分别为4,5,6,且这组数据的平均数为4,则这组数据的中位数为( )A、4.5 B、5.5 C、5 D、46. 将直线y=3x﹣1向上平移2个单位长度,平移后的直线所对应的函数解析式为( )A、y=3x+5 B、y=3x﹣3 C、y=3x+1 D、y=3x+37. 如图,直线y=﹣ 分别交x轴于点A,y轴于点B,点D、E分别是线段AB、AO的中点,连结DE,则DE的长是( ) A、4 B、2 C、1 D、8. 如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连结CE.若∠AFD=56°,则∠CEF的度数为( )
A、4 B、2 C、1 D、8. 如图,在正方形ABCD中,E是对角线BD上一点,AE的延长线交CD于点F,连结CE.若∠AFD=56°,则∠CEF的度数为( ) A、22° B、24° C、26° D、28°9. 如图,在菱形 中,P是对角线 上一动点,过点P作 于点E. 于点F.若菱形 的周长为20,面积为24,则 的值为( )
A、22° B、24° C、26° D、28°9. 如图,在菱形 中,P是对角线 上一动点,过点P作 于点E. 于点F.若菱形 的周长为20,面积为24,则 的值为( ) A、4 B、 C、6 D、10. 如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( ).
A、4 B、 C、6 D、10. 如图,在长方形ABCD中,AB=2,BC=1,运点P从点B出发,沿路线B→C→D作匀速运动,那么△ABP的面积y与点P运动的路程x之间的函数图象大致是( ).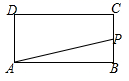 A、
A、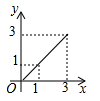 B、
B、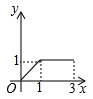 C、
C、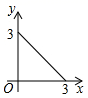 D、
D、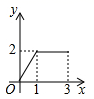
二、填空题
-
11. 在函数y=中,自变量x的取值范围是 .
12. 如图,在▱ABCD中,对角线AC、BD相交于点O,在不添加任何辅助线的情况下,请你添加一个条件 , 使▱ABCD是菱形. 13. 从甲、乙两人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86.5分,方差分别是S甲2=1.5,S乙2=2.6,你认为更合适去参赛的是 . (填“甲”或“乙”)14. 若实数x,y满足 ,则xy﹣3的值为 .15. 已知菱形ABCD中,∠ABC=60°,一条对角线长为6,则菱形的边长为 .16. 如图,点E在正方形ABCD的对角线AC上,连结DE,点O是AC的中点,点F是DE的中点,连结OF.若AC=8,CE=2,则OF的长为 .
13. 从甲、乙两人中选一人参加诗词大会比赛,经过三轮初赛,他们的平均成绩都是86.5分,方差分别是S甲2=1.5,S乙2=2.6,你认为更合适去参赛的是 . (填“甲”或“乙”)14. 若实数x,y满足 ,则xy﹣3的值为 .15. 已知菱形ABCD中,∠ABC=60°,一条对角线长为6,则菱形的边长为 .16. 如图,点E在正方形ABCD的对角线AC上,连结DE,点O是AC的中点,点F是DE的中点,连结OF.若AC=8,CE=2,则OF的长为 . 17. 如图,矩形ABCD的面积为17cm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOn﹣1CnB的面积为cm2 .
17. 如图,矩形ABCD的面积为17cm2 , 对角线交于点O;以AB、AO为邻边作平行四边形AOC1B,对角线交于点O1;以AB、AO1为邻边作平行四边形AO1C2B;…;以此类推,则平行四边形AOn﹣1CnB的面积为cm2 .
三、解答题
-
18. 计算:(1)、 ;(2)、 .19. 如图,在正方形网格中,每个小正方形的边长均为1,点A、B、C都在格点上.
 (1)、请直接写出线段AB、AC的长度;(2)、连结BC,请判断△ABC的形状,并说明理由.20. 如图,在▱ABCD中,AE,CF分别平分∠BAD和∠DCB,交对角线BD于点E,F.
(1)、请直接写出线段AB、AC的长度;(2)、连结BC,请判断△ABC的形状,并说明理由.20. 如图,在▱ABCD中,AE,CF分别平分∠BAD和∠DCB,交对角线BD于点E,F. (1)、若∠BCF=60°,求∠ABC的度数;(2)、连结AF、CE,则四边形AECF(填“是”或“不是”)平行四边形.21. 某校为了了解初中学生每天的睡眠时间(单位:h),随机调查了该校的部分初中学生,根据调查结果,绘制出如图所示的统计图.
(1)、若∠BCF=60°,求∠ABC的度数;(2)、连结AF、CE,则四边形AECF(填“是”或“不是”)平行四边形.21. 某校为了了解初中学生每天的睡眠时间(单位:h),随机调查了该校的部分初中学生,根据调查结果,绘制出如图所示的统计图.
请根据相关信息,解答下列问题:
(1)、本次接受调查的初中学生人数为 . 扇形统计图中的m= . 条形统计图中的n= .(2)、所调查的初中学生每天睡眠时间的众数是 .(3)、该校共有1600名初中学生,根据样本数据,估计该校初中学生每天睡眠时间不足8h的人数.22. 一辆货车从A地出发将一批物资运往B地,以80千米/时的速度行驶到中途的服务区C地休息了一段时间,然后提高车速继续向B地行驶,到达B地后用30分钟卸完物资.货车距A地的路程y(千米)与货车离开A地后经过的时间x(小时)的函数关系如图所示,请结合图象信息,解答下列问题: (1)、A,B两地的路程为千米,a= .(2)、货车在服务区C地休息了小时,b= .(3)、求货车离开A地后,经过多少小时距A地300千米?23. 在综合与实践活动课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动,如图1,现有矩形纸片ABCD,AB=4,BC=7.
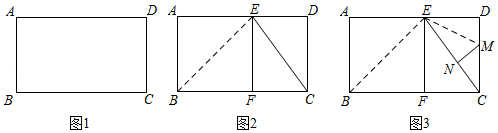
(1)、A,B两地的路程为千米,a= .(2)、货车在服务区C地休息了小时,b= .(3)、求货车离开A地后,经过多少小时距A地300千米?23. 在综合与实践活动课上,老师组织同学们以“矩形纸片的折叠”为主题开展数学活动,如图1,现有矩形纸片ABCD,AB=4,BC=7.动手操作
将图1中的矩形纸片折叠,使点A落在BC边上的点F处,然后展平,得到折痕BE,连结EF,EC,如图2.
解决问题
请根据图2完成下列问题:
(1)、线段CF的长为 .线段CE的长为 .(2)、试判断四边形ABFE的形状,并给予证明.(3)、将图2中的矩形纸片再次折叠,使点D落在CE上的点N处,然后展平,得到折痕EM,连结MN,如图3,则线段CM的长为 .24. 如图,直线l1:y=x+3与过点A(3,0)的直线l2交于点C(1,m),与x轴交于点B. (1)、求直线l2对应的函数解析式;(2)、求△ABC的面积;(3)、请你找到图象中直线l1在直线l2上方的部分,直接写出此时自变量x的取值范围;(4)、在坐标平面内是否存在点P,使以点A、B、C、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
(1)、求直线l2对应的函数解析式;(2)、求△ABC的面积;(3)、请你找到图象中直线l1在直线l2上方的部分,直接写出此时自变量x的取值范围;(4)、在坐标平面内是否存在点P,使以点A、B、C、P为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.