黑龙江省鹤岗市萝北县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 在学校举办的“中华诗词大赛”中,有11名选手进入决赛,他们的决赛成绩各不相同,其中一名参赛选手想知道自己是否能进入前6名,他需要了解这11名学生成绩的( )A、中位数 B、平均数 C、众数 D、方差3. 小张的爷爷每天坚持体育锻炼,星期天爷爷从家里跑步到公园,打了一会太极拳,然后沿原路慢步走到家,下面能反映当天爷爷离家的距离y(米)与时间t(分钟)之间关系的大致图象是( )A、
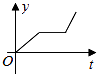 B、
B、 C、
C、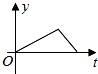 D、
D、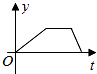 4. 若直角三角形的两条直角边长分别为 、 ,则该直角三角形斜边上的中线为( )A、 B、 C、 D、5. 由下列线段a,b,c可以组成直角三角形的是( ).A、a=1,b=2,c=3 B、a=b=1,c= C、a=4,b=5,c=6 D、a=2,b=2 ,c=46. 如图为一次函数y=kx+b(k≠0)的图象,则下列正确的是( )
4. 若直角三角形的两条直角边长分别为 、 ,则该直角三角形斜边上的中线为( )A、 B、 C、 D、5. 由下列线段a,b,c可以组成直角三角形的是( ).A、a=1,b=2,c=3 B、a=b=1,c= C、a=4,b=5,c=6 D、a=2,b=2 ,c=46. 如图为一次函数y=kx+b(k≠0)的图象,则下列正确的是( ) A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<07. 在四边形 中 , , 且 ,则四边形 的面积( )
A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<07. 在四边形 中 , , 且 ,则四边形 的面积( ) A、1 B、2 C、3 D、48. 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
A、1 B、2 C、3 D、48. 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( ) A、3和2 B、2和3 C、4和1 D、1和49. 如图,在正方形 的外侧,作等边 ,连接 、 ,线段 与 相交于点 ,则 的大小为( )
A、3和2 B、2和3 C、4和1 D、1和49. 如图,在正方形 的外侧,作等边 ,连接 、 ,线段 与 相交于点 ,则 的大小为( ) A、55° B、60° C、67.5° D、75°10. 如图,已知在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下面结论中:①图形中全等的三角形只有三对;②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF= OA;⑤ =2OP·OB.正确结论的个数是( )
A、55° B、60° C、67.5° D、75°10. 如图,已知在正方形ABCD中,点O为对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,则下面结论中:①图形中全等的三角形只有三对;②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF= OA;⑤ =2OP·OB.正确结论的个数是( ) A、4个 B、3个 C、2个 D、1个
A、4个 B、3个 C、2个 D、1个二、填空题
-
11. 函数 中,自变量x的取值范围是 .12. 若 是关于 的正比例函数,则常数 .13.
如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件 ,可
得平行四边形ABCD是矩形.
 14. 若a<1,化简 =.15. 八年级甲班与乙班各选出20名学生进行英文打字比赛,通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的平均数相同,甲班成绩的方差为17.5,乙班成绩的方差为15.由此可知班的成绩稳定.16. 如图,在平面直角坐标系中,菱形 的顶点 坐标是 ,则顶点 的坐标是 .
14. 若a<1,化简 =.15. 八年级甲班与乙班各选出20名学生进行英文打字比赛,通过对参赛学生每分钟输入的单词个数进行统计,两班成绩的平均数相同,甲班成绩的方差为17.5,乙班成绩的方差为15.由此可知班的成绩稳定.16. 如图,在平面直角坐标系中,菱形 的顶点 坐标是 ,则顶点 的坐标是 . 17. 如图,矩形 的对角线 和 相交于点O,过点O的直线分别交 和 于点E、F,且 , ,那么图中阴影部分的面积为 .
17. 如图,矩形 的对角线 和 相交于点O,过点O的直线分别交 和 于点E、F,且 , ,那么图中阴影部分的面积为 . 18. 如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是dm.
18. 如图是一个三级台阶,它的每一级的长、宽和高分别为20 dm,3 dm,2 dm,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点的最短路程是dm.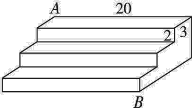 19. 在平面直角坐标系中,已知一次函数 的图象经过 , 两点,则 (填“ ”“ ”或“ ”).20. 如图,菱形 的边长为1, ;作 于点 ,以 为一边,做第二个菱形 ,使 ;作 于点 ,以 为一边做第三个菱形 ,使 ;……依此类推,这样做的第n个菱形 的边
19. 在平面直角坐标系中,已知一次函数 的图象经过 , 两点,则 (填“ ”“ ”或“ ”).20. 如图,菱形 的边长为1, ;作 于点 ,以 为一边,做第二个菱形 ,使 ;作 于点 ,以 为一边做第三个菱形 ,使 ;……依此类推,这样做的第n个菱形 的边的长是.

三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 如图,已知 、 分别是平行四边形 的边 、 上的两点,且 .
 (1)、求证: ;(2)、判定四边形 是否是平行四边形?23. 已知一次函数 图象经过点 和点 ,
(1)、求证: ;(2)、判定四边形 是否是平行四边形?23. 已知一次函数 图象经过点 和点 , (1)、求这个函数解析式;(2)、求一次函数与坐标轴围成的三角形的面积;(3)、当 取何值时, ?24. 某区对参加2010年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分,请根据图表信息回答下列问题:
(1)、求这个函数解析式;(2)、求一次函数与坐标轴围成的三角形的面积;(3)、当 取何值时, ?24. 某区对参加2010年中考的5000名初中毕业生进行了一次视力抽样调查,绘制出频数分布表和频数分布直方图的一部分,请根据图表信息回答下列问题:视力
频数(人)
频率
20
0.1
40
0.2
70
0.35
a
0.3
10
b
 (1)、在频数分布表中, 的值为 , 的值为 , 并将频数分布直方图补充完整;(2)、甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?(3)、若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 , 并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?25. 已知 、 两地相距100千米,甲、乙两人骑车同时分别从 、 两地相向而行.假设他们都保持匀速行使,则他们各自到 地的距离 (千米)都是骑车时间 (时)的一次函数.
(1)、在频数分布表中, 的值为 , 的值为 , 并将频数分布直方图补充完整;(2)、甲同学说“我的视力情况是此次抽样调查所得数据的中位数”,问甲同学的视力情况应在什么范围内?(3)、若视力在4.9以上(含4.9)均属正常,则视力正常的人数占被统计人数的百分比是 , 并根据上述信息估计全区初中毕业生中视力正常的学生有多少人?25. 已知 、 两地相距100千米,甲、乙两人骑车同时分别从 、 两地相向而行.假设他们都保持匀速行使,则他们各自到 地的距离 (千米)都是骑车时间 (时)的一次函数. (1)、甲的速度为 , 乙的速度为;(2)、求出: 和 的关系式;(3)、问经过多长时间两人相遇.26. 在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.
(1)、甲的速度为 , 乙的速度为;(2)、求出: 和 的关系式;(3)、问经过多长时间两人相遇.26. 在菱形ABCD中,∠ABC=60°,E是对角线AC上一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.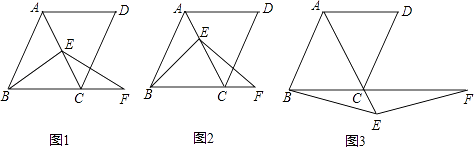 (1)、若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(1)、若E是线段AC的中点,如图1,易证:BE=EF(不需证明);
(2)、若E是线段AC或AC延长线上的任意一点,其它条件不变,如图2、图3,线段BE,EF有怎样的数量关系,直接写出你的猜想;并选择一种情况给予证明.27. 某学校为改善办学条件,计划采购A、B两种型号的空调,已知采购3台A型空调和2台B型空调,需费用39000元;4台A型空调比5台B型空调的费用多6000元.
(1)、求A型空调和B型空调每台各需多少元;
(2)、若学校计划采购A、B两种型号空调共30台,且A型空调的台数不少于B型空调的一半,两种型号空调的采购总费用不超过217000元,该校共有哪几种采购方案?
(3)、在(2)的条件下,采用哪一种采购方案可使总费用最低,最低费用是多少元?28. 如图,平面直角坐标系中,直线 经过点 , ,点 是第一象限的点且 ,过点 作 轴,垂足为 , . (1)、直线 的解析式;(2)、求点 坐标;(3)、若点 是直线 上的一个动点,在 轴上存在另一个点 ,且以 、 、 、 为顶点的四边形是平行四边形,请直接写出点 的坐标.
(1)、直线 的解析式;(2)、求点 坐标;(3)、若点 是直线 上的一个动点,在 轴上存在另一个点 ,且以 、 、 、 为顶点的四边形是平行四边形,请直接写出点 的坐标.