黑龙江省哈尔滨市道里区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列选项中的方程，是一元二次方程的为（）

A、x+ $\frac{1}{x^{2}}$ ＝1 B、x²+2y﹣3＝0 C、3x²＝1 D、x³﹣2x+1＝0

查看试题解析
2. 线段a、b、c组成的三角形不是直角三角形的是（　　）

A、a＝7，b＝24，c＝25 B、a＝ $\sqrt{41}$ ，b＝4，c＝5 C、a＝ $\frac{5}{4}$ ，b＝1，c＝ $\frac{3}{4}$ D、a＝40，b＝50，c＝60

查看试题解析
3. 下列命题错误的是（）

A、对角线互相平分的四边形是平行四边形 B、对角线相等的平行四边形是矩形 C、一条对角线平分一组对角的四边形是菱形 D、对角线互相垂直的矩形是正方形

查看试题解析
4. 如图，在菱形ABCD中，对角线AC、BD相交于点O，E为AB的中点，且OE=2，则菱形ABCD的周长为（）

A、12 B、16 C、8 D、4

查看试题解析
5. 已知点（－1，y₁），（4，y₂）在一次函数y＝3x－2的图象上，则y₁ ， y₂ ， 0的大小关系是（）

A、0＜y₁＜y₂ B、y₁＜0＜y₂ C、y₁＜y₂＜0 D、y₂＜0＜y₁

查看试题解析
6. 某商店今年1月份的销售额是2万元，3月份的销售额是4.5万元，从1月份到3月份，该店销售额平均每月的增长率是（）

A、20% B、25% C、50% D、62.5%

查看试题解析
7. 如图，在矩形纸片ABCD中，AB=3，点E在边BC上，将△ABE沿直线AE折叠，点B恰好落在对角线AC上的点F处，若∠EAC=∠ECA，则AC的长是（）

A、 $3 \sqrt{3}$ B、6 C、4 D、5

查看试题解析
8. 若关于x的一元二次方程 $k x^{2} - 2 x - 1 = 0$ 有两个不相等的实数根，则实数k的取值范围是（）

A、 $k > - 1$ B、 $k > - 1$ 且 $k \neq 0$ C、 $k < - 1$ D、 $k < - 1$ 或 $k = 0$

查看试题解析
9. 如图，点E为正方形ABCD的边CD的中点，DE＝5，则BE的长为（）

A、13 B、12 C、5 $\sqrt{5}$ D、10 $\sqrt{5}$

查看试题解析
10. A，B两地相距200千米的路程．货车甲从A地出发将一批物资运往B地，匀速行驶一段路程后出现故障，即刻停车与B地联系．B地收到消息后立即派货车乙从B地出发匀速行进去接运甲车上的物资．货车乙遇到货车甲后，用了18分钟将物资从货车甲搬运到货车乙上，随后开往B地．两辆货车距离各自出发地的路程y（千米）与甲车离开A地时间x（小时）的函数关系如图所示，（通话等其他时间忽略不计）以下四个结论错误的是（）

A、货车甲从出发到出现故障前的速度为50千米/时 B、货车乙从出发到遇到货车甲前的速度为80千米/时 C、货车乙从出发到遇到货车甲用3.1小时 D、物资由货车甲全部搬运到货车乙上时，甲货车已经出发3.4小时

查看试题解析

二、填空题

11. 函数y= $\frac{x - 2}{x + 3}$ 中，自变量x的取值范围是

查看试题解析
12. 若正比例函数y＝kx的图象经过点（2，﹣4），则k的值为．

查看试题解析
13. 在△ABC中，AB＝13，BC＝10，BC边上的中线AD＝12，则△ABC的周长为．

查看试题解析
14. x＝2是关于x的一元二次方程ax²﹣4x﹣4＝0的一个根，则a的值为．

查看试题解析
15. 如图，在平行四边形ABCD中，∠B＝60°，∠BCD的平分线交AD于点E，若CD＝6，四边形ABCE的周长为26，则BC长为．

查看试题解析
16. 函数y=﹣2x+3的图象不经过第象限.

查看试题解析
17. 四边形ABCD为菱形，该菱形的周长为8，面积为2，则∠ABC为度．

查看试题解析
18. 参加足球联赛的每两队之间都进行两场比赛，共要比赛210场，则参加比赛的足球队共有个．

查看试题解析
19. 如图，矩形ABCD，AB＝4，AD＝7，点E在BC上，CE＝CD，DF⊥AE，点F为垂足，则DF的长为．

查看试题解析
20. 如图，在正方形ABCD的外侧，作等边三角形ADE，AC，BE相交于点F，则∠BFC为°.

查看试题解析

三、解答题

21. 解下列方程：

(1)、 $x^{2} - 3 x = 0$

(2)、 $5 x^{2} - 4 x - 1 = 0$ .

查看试题解析
22. 如图，每个小正方形的边长都为1，AB的位置如图所示．

(1)、在图中确定点C，请你连接CA，CB，使CB⊥BA，AC＝5；

(2)、在完成（1）后，在图中确定点D，请你连接DA，DC，DB，使CD＝ $\sqrt{10}$ ，AD＝ $\sqrt{17}$ ，直接写出BD的长．

查看试题解析
23. 如图，在平面直角坐标系中，点O为坐标原点，直线y＝2x﹣1与直线y＝ $\frac{3}{4}$ x+ $\frac{3}{2}$ 交于点A，过点A作x轴的垂线，点B为垂足，点C的横坐标为﹣1，点C在直线y＝2x﹣1上，连接BC．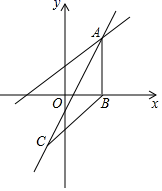

(1)、求点A的坐标；

(2)、求∠CBO的度数．

查看试题解析
24. 如图，点E，F分别在正方形ABCD的边CD，BC上，AE与DF交于点G，∠AGD＝90°．

(1)、求证：AE＝DF；

(2)、若AG＝4GE，在不添加任何辅助线的情况下，请写出图中所有长度等于AB一半的线段．

查看试题解析
25. 已知某列货车挂有A，B两种不同规格的货车厢共60节，使用A型车厢每节费用为6000元，使用B型车厢每节费用为8000元，设使用该列车全部车厢的总费用为y万元，这列货车挂A型车厢x节．

(1)、试写出y与x之间的函数关系式；

(2)、若使用该列车全部车厢的总费用少于45万元，则至少挂A型车厢多少节？

查看试题解析
26. 四边形ABCD，AD∥BC，∠ABC＝∠D．

(1)、如图（1），求证：四边形ABCD为平行四边形；

(2)、如图（2），过A，C两点分别作AE⊥BC，CF⊥AD，E，F为垂足．求证：BE＝DF；

(3)、如图（3），在（2）的条件下，点G在AC上，点H为四边形ABCD所在平面内一点，∠BHG＝∠D＝60°，∠AHG＝30°，∠ACB＝2∠AGH，BC＝8，AG＝5，求AF长．

查看试题解析
27. 在平面直角坐标系中，点O为坐标原点，过点B的直线y＝﹣ $\frac{4}{3}$ x+ $\frac{16}{3}$ 交x轴于点A，点B的横坐标为1，点C在x轴负半轴，OC＝1．

(1)、如图（1），求直线BC的解析式；

(2)、如图（2），点P在直线BC上，点P的横坐标为t，点P在第三象限，过点P作x轴的平行线交直线AB于点Q，设PQ的长为d，求d与t之间的函数关系式，不要求写出自变量t的取值范围；

(3)、如图（3），在（2）的条件下，点D在PQ上，CD⊥BC，∠BDA＝45°，求d的值．

查看试题解析