河北省石家庄市赞皇县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 下列二次根式中,最简二次根式是( )A、 B、 C、 D、2. 函数 的自变 的取值范围是( )A、 B、 C、 D、 且3. 下列四组线段不能围成直角三角形的是( )A、a=8,b=15,c=17 B、a=9,b=12,c=15 C、a=3,b=4,c=5 D、a=4,b=6,c=114. 下列各式正确的是( )A、 =±5 B、 =﹣3 C、± =3 D、 =﹣25. 甲、乙两人进行射击测试,每人10次射击,两人射击平均成绩均为9.2环,方差分别为S甲2、S乙2 , 若甲的成绩更稳定,则S甲2、S乙2的大小关系为( )A、S甲2>S乙2 B、S甲2<S乙2 C、S甲2=S乙2 D、无法确定6. 已知一次函数 ,若 ,则该函数的图象可能是( )A、
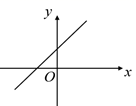 B、
B、 C、
C、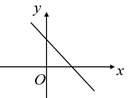 D、
D、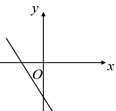 7. 已知平行四边形ABCD中,∠A比∠B小40°,那么∠C的度数是( )A、40° B、70° C、110° D、140°8. 下列关于四边形的说法,正确的是( )A、四个角相等的四边形是菱形 B、对角线互相垂直的四边形是矩形 C、有两边相等的平行四边形是菱形 D、两条对角线相等的平行四边形是矩形9. 如图,某公园内的一块草坪是长方形 ,已知 ,公园管理处为了方便群众,沿 修了一条近道.一个人从A到C走 比直接走 多走了( )
7. 已知平行四边形ABCD中,∠A比∠B小40°,那么∠C的度数是( )A、40° B、70° C、110° D、140°8. 下列关于四边形的说法,正确的是( )A、四个角相等的四边形是菱形 B、对角线互相垂直的四边形是矩形 C、有两边相等的平行四边形是菱形 D、两条对角线相等的平行四边形是矩形9. 如图,某公园内的一块草坪是长方形 ,已知 ,公园管理处为了方便群众,沿 修了一条近道.一个人从A到C走 比直接走 多走了( )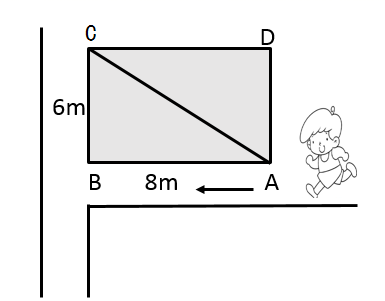 A、2米 B、4米 C、6米 D、8米10. 如图,直线 上有三个正方形 、 、 ,若正方形 、 的边长分别为5和7,则正方形 的面积为( )
A、2米 B、4米 C、6米 D、8米10. 如图,直线 上有三个正方形 、 、 ,若正方形 、 的边长分别为5和7,则正方形 的面积为( )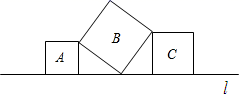 A、36 B、49 C、74 D、8111. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm , 接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )
A、36 B、49 C、74 D、8111. 小明用四根长度相同的木条制作了能够活动的菱形学具,他先活动学具成为图1所示菱形,并测得∠B=60°,对角线AC=20cm , 接着活动学具成为图2所示正方形,则图2中对角线AC的长为( )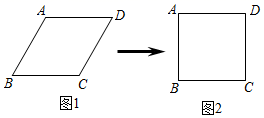 A、20cm B、30cm C、40cm D、20 cm12. 正比例函数y=2x的图象经过点A(3,m),B(﹣2,n),则m与n的大小关系是( )A、m>n B、m<n C、m=n D、无法确定13. 若函数y= , 则当函数值y=8时,自变量x的值是( )
A、20cm B、30cm C、40cm D、20 cm12. 正比例函数y=2x的图象经过点A(3,m),B(﹣2,n),则m与n的大小关系是( )A、m>n B、m<n C、m=n D、无法确定13. 若函数y= , 则当函数值y=8时,自变量x的值是( )
A、± B、4 C、±或4 D、4或-14. 直线l1:y=k1x+b与直线l2:y=k2x在同一平面直角坐标系中的图象如图所示,直线l1:y=k1x+b交x轴于点(﹣3,0),则关于x的不等式k2x<k1x+b<0的解集为( )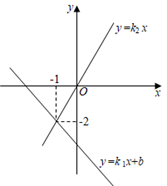 A、﹣3<x<﹣1 B、﹣2<x<﹣1 C、﹣3<x<1 D、﹣1<x<215. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )
A、﹣3<x<﹣1 B、﹣2<x<﹣1 C、﹣3<x<1 D、﹣1<x<215. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )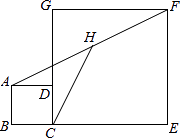 A、2.5 B、 C、 D、216. 如图中的图象(折线ABCDE)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法:
A、2.5 B、 C、 D、216. 如图中的图象(折线ABCDE)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法:①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为 千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法有( )
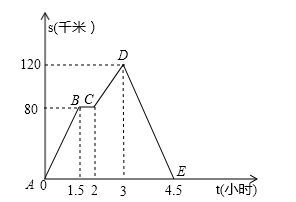 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题
-
17. 比较大小:18. 如图,AC是菱形ABCD的对角线,P是AC上的一个动点,过点P分别作AB和BC的垂线,垂足分别是点F和E,若菱形的周长是12cm,面积是6cm2 , 则PE+PF的值是cm.
 19. 如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交ll于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点作y轴的垂线交l2于点A4 , …依次进行下去.则点A4的坐标为;点 的坐标为;点A2021的坐标为 .
19. 如图,在平面直角坐标系中,函数y=2x和y=﹣x的图象分别为直线l1 , l2 , 过点(1,0)作x轴的垂线交ll于点A1 , 过点A1作y轴的垂线交l2于点A2 , 过点A2作x轴的垂线交l1于点A3 , 过点作y轴的垂线交l2于点A4 , …依次进行下去.则点A4的坐标为;点 的坐标为;点A2021的坐标为 .
三、解答题
-
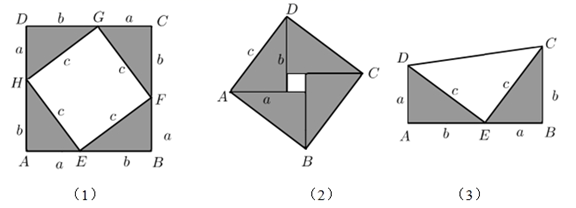
20. 已知x= + ,y= ﹣ ,求:(1)、 的值;(2)、) + 的值.21. 勾股定理是毕达哥拉斯定理的中国称谓,它揭示了直角三角形三边的数量关系:直角三角形两直角边的平方和等于斜边的平方,中国是发现、研究和运用勾股定理最古老的国家之一,我国古称直角三角形的直角边为“勾”或“股”,斜边为“弦”,因而将这条定理称为勾股定理.请你从以下图形中,任意选择一个来证明这个定理.

 22. 在信息技术考试中,初二某班除两名同学因故未参加外,其余同学全部参加考试,考试结束后,把得到的成绩(均为整数分,满分10分)进行统计并制成如图1所示的条形统计图和如图2所示的扇形统计图(不完整).
22. 在信息技术考试中,初二某班除两名同学因故未参加外,其余同学全部参加考试,考试结束后,把得到的成绩(均为整数分,满分10分)进行统计并制成如图1所示的条形统计图和如图2所示的扇形统计图(不完整).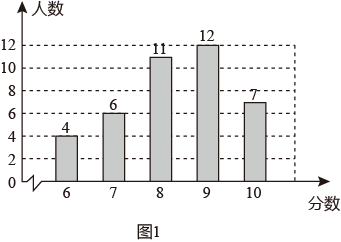
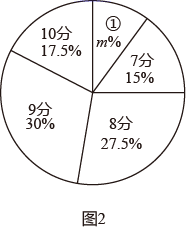 (1)、 ;(2)、图2中9分成绩所在扇形对应的圆心角的度数为 ;(3)、这组数据的平均数;中位数 ;众数 ;(4)、若两名同学经过补测,把得到的成绩与原来成绩合并后,发现成绩的中位数发生改变,求这两名同学的成绩和.23. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.
(1)、 ;(2)、图2中9分成绩所在扇形对应的圆心角的度数为 ;(3)、这组数据的平均数;中位数 ;众数 ;(4)、若两名同学经过补测,把得到的成绩与原来成绩合并后,发现成绩的中位数发生改变,求这两名同学的成绩和.23. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于F,且AF=BD,连接BF.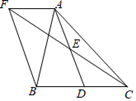 (1)、求证:BD=DC.(2)、若AB=AC时,试证明四边形AFBD是矩形.24. 问题探究:嘉嘉同学根据学习函数的经验,对函数y=-2|x|+5的图象和性质进行了探究.下面是嘉嘉的探究过程,请你解决相关问题:
(1)、求证:BD=DC.(2)、若AB=AC时,试证明四边形AFBD是矩形.24. 问题探究:嘉嘉同学根据学习函数的经验,对函数y=-2|x|+5的图象和性质进行了探究.下面是嘉嘉的探究过程,请你解决相关问题:(Ⅰ)在函数y=-2|x|+5中,自变量x可以是任意实数;
(Ⅱ)如下表是y与x的几组对应值:
x
…
-4
-3
-2
-1
0
1
2
3
4
…
y
…
-3
-1
1
3
5
3
1
-1
-3
…
(1)、如图,嘉嘉同学在平面直角坐标系中,描出了以表中各对对应值为坐标的点,请你根据描出的点,画出该函数的图象:
若A(m,n),B(6,n)为该函数图象上不同的两点,则m=;
(2)、观察函数y=-2|x|+5的图象,写出该图象的两条性质;(3)、直接写出,当0<-2|x|+5≤3时,自变量x的取值范围.25. 能够完全重合的平行四边形纸片ABCD和AEFG按图①方式摆放,其中AD=AG=5,AB=AE=9.点D,G分别在边AE,AB上,CD与FG相交于点H.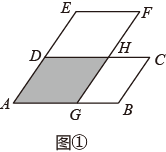
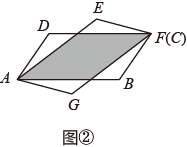
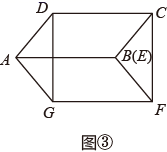 (1)、(探究)求证:四边形AGHD是菱形.(2)、(操作一)固定图①中的平行四边形纸片ABCD,将平行四边形纸片AEFG绕着点A顺时针旋转一定的角度,使点F与点C重合,如图②.则这两张平行四边形纸片未重叠部分图形的周长和为 .(3)、(操作二)将图②中的平行四边形纸片AEFG绕着点A继续顺时针旋转一定的角度,使点E与点B重合,连接DG,CF,如图③,若∠BAD= ,求四边形DCFG的面积.26. 众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到A地和B地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
(1)、(探究)求证:四边形AGHD是菱形.(2)、(操作一)固定图①中的平行四边形纸片ABCD,将平行四边形纸片AEFG绕着点A顺时针旋转一定的角度,使点F与点C重合,如图②.则这两张平行四边形纸片未重叠部分图形的周长和为 .(3)、(操作二)将图②中的平行四边形纸片AEFG绕着点A继续顺时针旋转一定的角度,使点E与点B重合,连接DG,CF,如图③,若∠BAD= ,求四边形DCFG的面积.26. 众志成城抗疫情,全国人民在行动.某公司决定安排大、小货车共20辆,运送260吨物资到A地和B地,支援当地抗击疫情.每辆大货车装15吨物资,每辆小货车装10吨物资,这20辆货车恰好装完这批物资.已知这两种货车的运费如下表:
A地(元/辆)
B地(元/辆)
大货车
900
1000
小货车
500
700
现安排上述装好物资的20辆货车(每辆大货车装15吨物资,每辆小货车装10吨物资)中的10辆前往A地,其余前往B地,设前往A地的大货车有x辆,这20辆货车的总运费为y元.
(1)、这20辆货车中,大货车、小货车各有多少辆?(2)、求 与 的函数解析式,并直接写出 的取值范围;(3)、若运往A地的物资不少于140吨,求总运费y的最小值.