河北省邯郸市大名县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 已知点P的坐标为 ,则点P到x轴的距离是A、1 B、2 C、 D、2. 要反映某市某一周每天的最高气温的变化趋势,宜采用( )A、条形统计图 B、扇形统计图 C、折线统计图 D、以上均可3. 函数y= 中自变量x的取值范围是( )A、x>2 B、x≥2 C、x≠2 D、x<24. 下列函数:① ;② ;③ ;④ ;⑤ .其中,是一次函数的有( )A、1个 B、2个 C、3个 D、4个5. 不能判定一个四边形是平行四边形的条件是()
A、两组对边分别平行 B、一组对边平行,另一组对边相等 C、一组对边平行且相等 D、两组对边分别相等6. 如图,D、E分别为△ABC边AC、BC的中点,∠A=60°,DE=6,则下列判断错误的是( ) A、∠ADE=120° B、AB=12 C、∠CDE=60° D、DC=67. 为了解某校八年级900名学生每天做家庭作业所用的时间,随机抽取其中120名学生进行抽样调查下列说法 正确的是( )A、该校八年级全体学生是总体 B、从中抽取的120名学生是个体 C、每个八年级学生是总体的一个样本 D、样本容量是1208. 在平面直角坐标系中,点 所在的象限是A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知多边形的内角和等于外角和的三倍,则这个多边形的边数为( )A、9 B、8 C、7 D、610. 如图是某手机店今年1﹣5月份音乐手机销售额统计图.根据图中信息,可以判断相邻两个月音乐手机销售额变化最大的是( )
A、∠ADE=120° B、AB=12 C、∠CDE=60° D、DC=67. 为了解某校八年级900名学生每天做家庭作业所用的时间,随机抽取其中120名学生进行抽样调查下列说法 正确的是( )A、该校八年级全体学生是总体 B、从中抽取的120名学生是个体 C、每个八年级学生是总体的一个样本 D、样本容量是1208. 在平面直角坐标系中,点 所在的象限是A、第一象限 B、第二象限 C、第三象限 D、第四象限9. 已知多边形的内角和等于外角和的三倍,则这个多边形的边数为( )A、9 B、8 C、7 D、610. 如图是某手机店今年1﹣5月份音乐手机销售额统计图.根据图中信息,可以判断相邻两个月音乐手机销售额变化最大的是( ) A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月11. 李雷同学周末晨练,他从家里出发,跑步到公园,然后在公园玩一会儿篮球,再走路回家,那么,他与自己家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )A、
A、1月至2月 B、2月至3月 C、3月至4月 D、4月至5月11. 李雷同学周末晨练,他从家里出发,跑步到公园,然后在公园玩一会儿篮球,再走路回家,那么,他与自己家的距离y(米)与时间x(分钟)之间的关系的大致图象是( )A、 B、
B、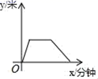 C、
C、 D、
D、 12. 如图,四边形ABCD的对角线为AC、BD,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( )
12. 如图,四边形ABCD的对角线为AC、BD,且AC=BD,则下列条件能判定四边形ABCD为矩形的是( ) A、BA=BC B、AC、BD互相平分 C、AC⊥BD D、AB∥CD13. 将点 向左平移 个单位长度,在向上平移 个单位长度得到点 ,则点 的坐标是( )A、 B、 C、 D、14. 在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )
A、BA=BC B、AC、BD互相平分 C、AC⊥BD D、AB∥CD13. 将点 向左平移 个单位长度,在向上平移 个单位长度得到点 ,则点 的坐标是( )A、 B、 C、 D、14. 在平面直角坐标系中,一次函数y=kx+b的图象如图所示,则k和b的取值范围是( )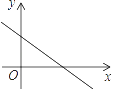 A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<015. 在一个三角形中,一个外角是其相邻内角的3倍,那么这个外角是( )A、150° B、135° C、120° D、100°16. 两个一次函数y=-x+5和y=﹣2x+8的图象的交点坐标是( )A、(3,2) B、(-3,2) C、(3,-2) D、(-3,-2)
A、k>0,b>0 B、k>0,b<0 C、k<0,b>0 D、k<0,b<015. 在一个三角形中,一个外角是其相邻内角的3倍,那么这个外角是( )A、150° B、135° C、120° D、100°16. 两个一次函数y=-x+5和y=﹣2x+8的图象的交点坐标是( )A、(3,2) B、(-3,2) C、(3,-2) D、(-3,-2)二、填空题
-
17. 点P(2,-5)关于x轴对称的点的坐标为18. 已知一个正比例函数的图象经过点(-1,2),则这个正比例函数的解析式是 .19. 已知点P(3﹣m,m)在第二象限,则m的取值范围是 .20. 如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处,连接A′C,则∠BA′C=度.

三、解答题
-
21. 已知一次函数的图象经过点 和 .(1)、求该函数图象与x轴的交点坐标;(2)、判断点 是否在该函数图象上.22. 如图,在▱ABCD中,AE⊥BD,CF⊥BD,垂足分别为E、F.求证:
 (1)、AE=CF;(2)、四边形AECF是平行四边形.23. 某中学为丰富综合实践活动,开设了四个实验室如下:A.物理;B.化学;C.信息;D.生物.为了解学生最喜欢哪个实验室,随机抽取了部分学生进行调查,每位被调查的学生都选择了一个自己最喜欢的实验室,调查后将调查结果绘制成了如图统计图,请根据统计图回答下列问题
(1)、AE=CF;(2)、四边形AECF是平行四边形.23. 某中学为丰富综合实践活动,开设了四个实验室如下:A.物理;B.化学;C.信息;D.生物.为了解学生最喜欢哪个实验室,随机抽取了部分学生进行调查,每位被调查的学生都选择了一个自己最喜欢的实验室,调查后将调查结果绘制成了如图统计图,请根据统计图回答下列问题 (1)、求这次被调查的学生人数.(2)、请将条形统计图补充完整.(3)、求出扇形统计图中B对应的圆心角的度数.24. 已知:如图,在 ABC中,AB=AC,AD⊥BC,AN为 ABC外角∠CAM的平分线,CE⊥AN.
(1)、求这次被调查的学生人数.(2)、请将条形统计图补充完整.(3)、求出扇形统计图中B对应的圆心角的度数.24. 已知:如图,在 ABC中,AB=AC,AD⊥BC,AN为 ABC外角∠CAM的平分线,CE⊥AN. (1)、求证:四边形ADCE为矩形;(2)、猜想当AD、BC满足怎样的数量关系时,四边形ADCE是正方形,并说明理由.25. 如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程 、 与时间 的关系,观察图象并回答下列问题:
(1)、求证:四边形ADCE为矩形;(2)、猜想当AD、BC满足怎样的数量关系时,四边形ADCE是正方形,并说明理由.25. 如图,分别表示甲步行与乙骑自行车(在同一条路上)行走的路程 、 与时间 的关系,观察图象并回答下列问题: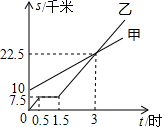 (1)、乙出发时,乙与甲相距千米;(2)、走了一段路程后,乙有事耽搁,停下来时间为小时;(3)、甲从出发起,经过 小时与乙相遇;(4)、甲行走的平均速度是多少千米 小时?26. 如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH.
(1)、乙出发时,乙与甲相距千米;(2)、走了一段路程后,乙有事耽搁,停下来时间为小时;(3)、甲从出发起,经过 小时与乙相遇;(4)、甲行走的平均速度是多少千米 小时?26. 如图,四边形ABCD为平行四边形,E为AD上的一点,连接EB并延长,使BF=BE,连接EC并延长,使CG=CE,连接FG.H为FG的中点,连接DH. (1)、求证:四边形AFHD为平行四边形;(2)、若CB=CE,∠BAE=70°,∠DCE=20°,求∠CBE的度数.27. 甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示.
(1)、求证:四边形AFHD为平行四边形;(2)、若CB=CE,∠BAE=70°,∠DCE=20°,求∠CBE的度数.27. 甲、乙两车分别从A、B两地同时出发,甲车匀速前往B地,到达B地立即以另一速度按原路匀速返回到A地;乙车匀速前往A地,设甲、乙两车距A地的路程为y(千米),甲车行驶的时间为x(时),y与x之间的函数图象如图所示. (1)、求甲车从A地到达B地的行驶时间;(2)、求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(1)、求甲车从A地到达B地的行驶时间;(2)、求甲车返回时y与x之间的函数关系式,并写出自变量x的取值范围;
(3)、求乙车到达A地时甲车距A地的路程.