河北省承德市兴隆县2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形具有稳定性的是（）

A、 B、 C、 D、

查看试题解析
2. 点P（2，5）关于x轴对称的点的坐标是（）

A、（﹣5，2） B、（﹣2，5） C、（﹣2，﹣5） D、（2，﹣5）

查看试题解析
3. 如图，点D、点E分别为AB、AC的中点，且DE=3，则BC之间的距离为（）

A、3 B、6 C、9 D、1.5

查看试题解析
4. 函数y $= \frac{1}{x + 1}$ 中自变量x的取值范围是（）

A、x≠0 B、x≥﹣1 C、x≠﹣1 D、x＜﹣1

查看试题解析
5. 下列哪组条件能判别四边形ABCD是平行四边形（）

A、AB $//$ CD ， AD=BC B、AB=CD ， AD=BC C、∠A=∠B ， ∠C=∠D D、AB=AD ， CB=CD

查看试题解析
6. 平面直角坐标系中，一个三角形的三个顶点的坐标，横坐标保持不变，纵坐标增加3个单位，则所得的图形与原图形相比（）．

A、形状不变，大小扩大了3倍 B、形状不变，向右平移了3个单位 C、形状不变，向上平移了3个单位 D、三角形被纵向拉伸为原来的3倍

查看试题解析
7.
在某次训练中，甲、乙两名射击运动员各射击10发子弹的成绩统计图如图所示，对于本次训练，有如下结论：①S_甲²＞S_乙²；②S_甲²＜S_乙²；③甲的射击成绩比乙稳定；④乙的射击成绩比甲稳定，由统计图可知正确的结论是（　　）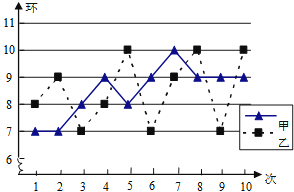

A、①③ B、①④ C、②③ D、②④

查看试题解析
8. 小明用50元钱去买单价是8元的笔记本，则他剩余的钱Q（元）与他买这种笔记本的本数x之间的函数关系式是（）

A、 $Q = 8 x$ B、 $Q = 8 x - 50$ C、 $Q = 8 x + 50$ D、 $Q = 50 - 8 x$

查看试题解析
9. 已知方程 $k x + b = 0$ 的解是 $x = 3$ ，则一次函数的图象可能是（）

A、 B、 C、 D、

查看试题解析
10. 下列说法错误的是（）

A、平行于x轴的直线上的所有点的纵坐标相同 B、点M（﹣2，1）与（2，﹣1）关于原点成中心对称 C、若点P（a，b）在x轴上，则a=0 D、（﹣3，4）与（4，﹣3）表示两个不同的点

查看试题解析
11. 下列关于平行四边形ABCD的叙述，正确的是（）

A、若AC＝BD，则平行四边形ABCD是矩形 B、若AB＝AD，则平行四边形ABCD是正方形 C、若AB⊥BC，则平行四边形ABCD是菱形 D、若AC⊥BD，则平行四边形ABCD是正方形

查看试题解析
12. 如图，菱形ABCD中， $∠ D = 150 °$ ，则 $∠ 1 =$ （）

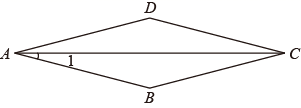A、30° B、25° C、20° D、15°

查看试题解析
13. 如图是小颖前三次购买苹果单价的统计图，第四次又买的苹果单价是a元/千克，发现这四个单价的中位数恰好也是众数，则a=（）

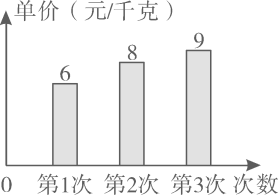A、9 B、8 C、7 D、6

查看试题解析
14. 有一个装水的容器，如图所示容器内的水面高度是10cm，现向容器内注水，并同时开始计时．在注水过程中，水面高度以每秒0.2cm的速度匀速增加，则容器注满水之前，容器内的水面高度与对应的注水时间满足的关系是（）

A、正比例函数关系 B、一次函数关系 C、不是函数关系 D、是函数关系但不能表达为具体函数

查看试题解析
15. 如图，AB $//$ CD，AD $//$ BE，点B、C、E在一直线上，连结AC、AE，则图中与△AED面积相等的三角形有（）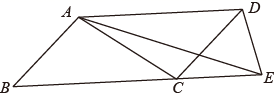

A、0个 B、1个 C、2个 D、3个

查看试题解析
16. 已知一组数据的方差s² $= \frac{1}{n}$ [（6﹣7）²+（10﹣7）²+（a﹣7）²+（b﹣7）²+（8﹣7）²]（a，b为常数），则a+b的值为（）

A、5 B、7 C、10 D、11

查看试题解析

二、填空题

17. 从一个多边形的一个顶点出发，一共可作9条对角线，则这个多边形的内角和是度．

查看试题解析
18. 如图，依据尺规作图的痕迹，计算∠α=°．

查看试题解析
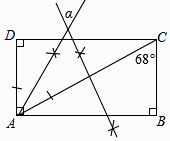19. 如图，在边长为10的正方形ABCD中，E，F分别为AD，BC的中点，P为对角线BD上的一个动点，则AF的长为， AP+EP的最小值的是．

查看试题解析

三、解答题

20. 一次函数的图象过点（﹣1，2）和点（ $\frac{1}{2}$ ，3），求这个函数的表达式．

查看试题解析
21. 小明就班级内所有学生的到校方式进行了一次调查，图（1）和图（2）是根据整理后的数据绘制的两幅不完整的统计图．

根据图中提供信息，解答以下问题：

(1)、求该班共有多少名学生？

(2)、求该班有多少名学生乘车到校？

(3)、在图（1）中，将表示“乘车”的部分补充完整；

(4)、求图（2）中，“步行”部分圆心角的度数．

查看试题解析
22. 如图，在正方形ABCD中，点P在对角线BD上，PE⊥BC，PF⊥CD，垂足分别为E、F．求证：AP=EF．

查看试题解析
23. 如图，直角坐标系xOy中，一次函数y $= - \frac{1}{2}$ x+5的图象l₁分别与x，y轴交于A，B两点，正比例函数的图象l₂与l₁交于点C（m，4）．

(1)、求m的值及l₂的解析式；

(2)、求△AOC的面积S_△AOC；

(3)、一次函数y=kx+1的图象与线段AC有交点，直接写出k的值．

查看试题解析
24. 如图，在菱形ABCD中，AB=2，∠ABC=60°，对角线AC、BD相交于点O，将对角线AC所在的直线绕点O顺时针旋转角α，（0°＜α＜90°）后得到直线l，直线l与AD、BC的两边相交于点E、F．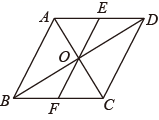

(1)、求证：△AOE≌△COF；

(2)、当α=30°时，求线段EF的长；

(3)、当α=60°时，直接写出四边形EOCD的面积．

查看试题解析
25. 有这样一个问题：探究函数y $= \frac{| x - 3 | + x + 3}{2}$ 的图象与性质．小东根据学习函数的经验，对函数y $= \frac{| x - 3 | + x + 3}{2}$ 的图象与性质进行了探究．

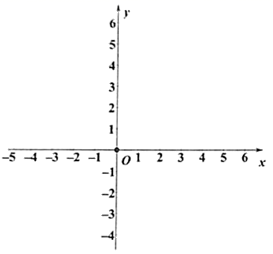
下面是小东的探究过程，请补充完成：

(1)、化简函数解析式，当x≥3时，y= ，当x＜3时，y=；

(2)、根据（1）中的结果，请在所给坐标系中画出函数y $= \frac{| x - 3 | + x + 3}{2}$ 的图象；

(3)、结合画出的函数图象，解决问题：若关于的方程x+a $= \frac{| x - 3 | + x + 3}{2}$ 有唯一解，直接写出实数a的取值范围：．

查看试题解析
26. 小张前往某精密仪器产应聘，公司承诺工资待遇如图，进厂后小张发现：加工1件A型零件和3件B型零件需5小时；加工2件A型零件和5件B型零件需9小时．
工资待遇：每月工资至少3000元；每天工作8小时，每月工作25天，加工1件A型零件计酬16元，加工1件B型零件计酬12元；月工资=底薪（800元）+计件工资．

(1)、小张加工1件A型零件和1件B型零件各需要多少小时？

(2)、若公司规定：小张每月必须加工A、B两种型号的零件，且加工B型的数量不大于A型零件数量的2倍，设小张每月加工A型零件a件，工资总额为W元，请你运用所学知识判断该公司颁布执行此规定后是否违背了工资待遇承诺？

查看试题解析