河北省承德市宽城满族自治县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 点(﹣4,2)所在的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 某同学要统计本班最受学生欢迎的社团活动,以下是排乱的统计步骤:
①从扇形图中分析出最受学生欢迎的社团活动
②制作问卷调查表,实施全班同学问卷调查
③绘制扇形图来表示各个社团所占的百分比
④整理问卷调查表并绘制频数分布表
正确统计步骤的顺序是( )
A、②→③→①→④ B、③→④→①→② C、①→②→④→③ D、②→④→③→①3. 刘师傅到加油站加油,如图是所用的加油机上的数据显示牌,则其中的变量是( ). A、金额 B、单价 C、数量 D、金额和数量4. 一个正多边形的每个外角都是36°,这个正多边形的边数是( )A、9 B、10 C、11 D、125. 已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )A、k>5 B、k<5 C、k>−5 D、k<−56. 如图,在平面直角坐标系中,菱形ABCD的顶点D在x轴上,边BC在y轴上,若点A的坐标为(12,13),则点B的坐标为( )
A、金额 B、单价 C、数量 D、金额和数量4. 一个正多边形的每个外角都是36°,这个正多边形的边数是( )A、9 B、10 C、11 D、125. 已知正比例函数y=(k+5)x,且y随x的增大而减小,则k的取值范围是( )A、k>5 B、k<5 C、k>−5 D、k<−56. 如图,在平面直角坐标系中,菱形ABCD的顶点D在x轴上,边BC在y轴上,若点A的坐标为(12,13),则点B的坐标为( ) A、 B、 C、 D、7. 如图,E , F是四边形ABCD两边AB , CD的中点,G , H是对角线AC , BD的中点,若EH=6,则以下结论错误的是( )
A、 B、 C、 D、7. 如图,E , F是四边形ABCD两边AB , CD的中点,G , H是对角线AC , BD的中点,若EH=6,则以下结论错误的是( ) A、 B、 C、 D、8. 若点A(3.5,y1),B(1.3,y2)都在直线y=3x﹣1上,则y1 , y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、无法比较大小9. 如图所示图象中,函数y=ax+a的图象可能是下列图象中的( )A、
A、 B、 C、 D、8. 若点A(3.5,y1),B(1.3,y2)都在直线y=3x﹣1上,则y1 , y2的大小关系是( )A、y1<y2 B、y1=y2 C、y1>y2 D、无法比较大小9. 如图所示图象中,函数y=ax+a的图象可能是下列图象中的( )A、 B、
B、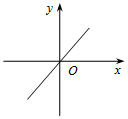 C、
C、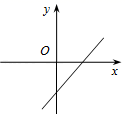 D、
D、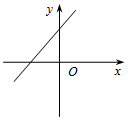 10. 下列说法中正确的是( )A、一组对边平行、一组对边相等的四边形是平行四边形 B、四个角都相等的四边形是矩形 C、菱形是轴对称图形不是中心对称图形 D、对角线垂直相等的四边形是正方形11. 海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是( )
10. 下列说法中正确的是( )A、一组对边平行、一组对边相等的四边形是平行四边形 B、四个角都相等的四边形是矩形 C、菱形是轴对称图形不是中心对称图形 D、对角线垂直相等的四边形是正方形11. 海平面上,有一个灯塔,测得海岛A在灯塔北偏东30°方向上,同时测得海岛B在灯塔北偏东60°的方向上,则灯塔的位置可以是( ) A、点O1 B、点O2 C、点O3 D、点O412. 等腰三角形的周长是40 cm,腰长y(cm)是底边长x(cm)的函数.此函数的表达式和自变量取值范围正确的是( )A、y=-2x+40(0<x<20) B、y=-0.5x+20(10<x<20) C、y=-2x+40(10<x<20) D、y=-0.5x+20(0<x<20)13. 如图,直线 经过点(2,0),则关于x的不等式 的解集是( )
A、点O1 B、点O2 C、点O3 D、点O412. 等腰三角形的周长是40 cm,腰长y(cm)是底边长x(cm)的函数.此函数的表达式和自变量取值范围正确的是( )A、y=-2x+40(0<x<20) B、y=-0.5x+20(10<x<20) C、y=-2x+40(10<x<20) D、y=-0.5x+20(0<x<20)13. 如图,直线 经过点(2,0),则关于x的不等式 的解集是( ) A、 B、 C、 D、14. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )
A、 B、 C、 D、14. 如图,在矩形ABCD中,AB=3,BC=4,动点P沿折线BCD从点B开始运动到点D,设点P运动的路程为x,△ADP的面积为y,那么y与x之间的函数关系的图象大致是( )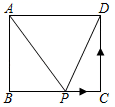 A、
A、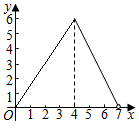 B、
B、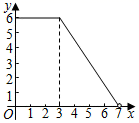 C、
C、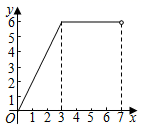 D、
D、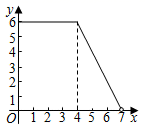 15. 如图,平行四边形ABCD的周长为52cm , 对角线AC与BD交于点O , 是BC的中点, 的周长比 的周长多6cm , 则AE的长度是( )
15. 如图,平行四边形ABCD的周长为52cm , 对角线AC与BD交于点O , 是BC的中点, 的周长比 的周长多6cm , 则AE的长度是( ) A、8cm B、5cm C、4cm D、3cm16. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形O ,依此方式,绕点O连续旋转2021次得到正方形O ,如果点A的坐标为(1,0),那么点 的坐标为( )
A、8cm B、5cm C、4cm D、3cm16. 如图,在平面直角坐标系中,将正方形OABC绕点O逆时针旋转45°后得到正方形O ,依此方式,绕点O连续旋转2021次得到正方形O ,如果点A的坐标为(1,0),那么点 的坐标为( )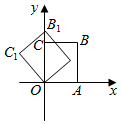 A、(1,1) B、(0, ) C、(0,﹣ ) D、(﹣1,1)
A、(1,1) B、(0, ) C、(0,﹣ ) D、(﹣1,1)二、填空题
-
17. 点P(3,﹣5)关于x轴对称的点的坐标为 .18. 如图,在矩形ABCD中,BE交AD于点E且平分∠ABC,对角线BD平分∠EBC,则 的值为 .
 19. 如图①,在平面上,边长为2的正方形和短边长为1的矩形对称中心重合.
19. 如图①,在平面上,边长为2的正方形和短边长为1的矩形对称中心重合. (1)、当正方形和矩形都水平放置时,重叠部分面积为 .(2)、当正方形不动,矩形绕着对称中心旋转,从图②到图③的过程中,重叠部分面积的大小 . (选择填写“不变”或“改变”)(3)、甲、乙两位同学分别给出了两个图形不同的重叠方式:
(1)、当正方形和矩形都水平放置时,重叠部分面积为 .(2)、当正方形不动,矩形绕着对称中心旋转,从图②到图③的过程中,重叠部分面积的大小 . (选择填写“不变”或“改变”)(3)、甲、乙两位同学分别给出了两个图形不同的重叠方式:甲:如图④,矩形绕着几何中心继续旋转,矩形的两条长边与正方形的对角线平行;
乙:如图⑤,将图④中的矩形向左上方平移,使矩形的一条长边恰好经过正方形的对角线;
在甲、乙两位同学给出的重叠方式中重叠部分面积小的是 . (选择填写“甲”或“乙”)
三、解答题
-
20. 定义新运算:对于任意实数 、 都有
例如 ,请根据上述知识解决下列问题:
(1)、 ,求 取值范围;(2)、若 ,求 的值;(3)、若方程 , 是一个常数,且此方程的一个解为 ,求 中的常数.21. 阅读材料:设a>0,b>0.∵( )2≥0,∴a﹣2 + ≥0,即a+ (当 = ,即a= 时,取“=”).由此可得结论:若a>0,b>0,则当a= 时,a+ 有最小值2 . (1)、理解概念:若x>0,则x=时,函数x+ 有最小值为 .(2)、拓展应用:若x>1,则代数式x+ 的最小值为 , 此时x=;(3)、解决问题:学校打算用篱笆围成一个长方形的生物园饲养小兔,生物园的一边AD靠墙(如图,墙足够长),面积为8m2 , 求至少需要多少米的篱笆?22. 《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了解学生对四大名著的阅读情况,就“四大古典名著”你读完了几部的问题在全校900名学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图,请根据以上信息,解决下列问题:
(1)、理解概念:若x>0,则x=时,函数x+ 有最小值为 .(2)、拓展应用:若x>1,则代数式x+ 的最小值为 , 此时x=;(3)、解决问题:学校打算用篱笆围成一个长方形的生物园饲养小兔,生物园的一边AD靠墙(如图,墙足够长),面积为8m2 , 求至少需要多少米的篱笆?22. 《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了解学生对四大名著的阅读情况,就“四大古典名著”你读完了几部的问题在全校900名学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图,请根据以上信息,解决下列问题: (1)、本次调查的学生名;(2)、求扇形统计图中1部所在扇形的圆心角的度数;(3)、请将条形统计图补充完整;(4)、试估算全校大约有多少学生读完了3部以上(含3部)名著.23. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作 , ,垂足分别为E,F.AC平分 .
(1)、本次调查的学生名;(2)、求扇形统计图中1部所在扇形的圆心角的度数;(3)、请将条形统计图补充完整;(4)、试估算全校大约有多少学生读完了3部以上(含3部)名著.23. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作 , ,垂足分别为E,F.AC平分 .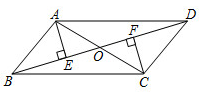 (1)、若 ,求 的度数;(2)、求证: .24. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示.
(1)、若 ,求 的度数;(2)、求证: .24. 一辆客车从甲地开往乙地,一辆出租车从乙地开往甲地,两车同时出发,设客车离甲地的距离为y1千米,出租车离甲地的距离为y2千米,两车行驶的时间为x小时,y1、y2关于x的函数图象如图所示. (1)、根据图象,求出y1、y2关于x的函数关系式;(2)、设两车之间的距离为S千米.
(1)、根据图象,求出y1、y2关于x的函数关系式;(2)、设两车之间的距离为S千米.①求两车相遇前S关于x的函数关系式;
②求出租车到达甲地后S关于x的函数关系式.
(3)、甲、乙两地间有A、B两个加油站,相距200千米,A加油站在甲地与B加油站之间,若两车相遇后,客车进入B加油站时,出租车恰好进入A加油站,求此时两车的行驶时间x的值和A加油站到甲地的距离.25. 为切实做好疫情防控工作,开学前夕,我县某校准备在民联药店购买口罩和水银体温计发放给每个学生.已知每盒口罩有100只,每盒水银体温计有10支,每盒口罩价格比每盒水银体温计价格多150元.用1200元购买口罩盒数与用300元购买水银体温计所得盒数相同.(1)、求每盒口罩和每盒水银体温计的价格各是多少元?(2)、如果给每位学生发放2只口罩和1支水银体温计,且口罩和水银体温计均整盒购买.设购买口罩m盒(m为正整数),则购买水银体温计多少盒能和口罩刚好配套?请用含m的代数式表示.(3)、在民联药店累计购医用品超过1800元后,超出1800元的部分可享受8折优惠.该校按(2)中的配套方案购买,共支付总费用w元;①当总费用不超过1800元时,求m的取值范围;并求w关于m的函数关系式.
②若该校有900名学生,按(2)中的配套方案购买,求所需总费用为多少元?
26. 如图1,在平面直角坐标系xOy中,直线y=﹣ x+ 与y=x相交于点A,与x轴交于点B,与y轴交于点C. (1)、求点A、B、C的坐标;(2)、如图1,若点D是线段OA上的点,且 COD的面积为 ,求直线CD的函数表达式;(3)、在直线OA上,是否存在一点E,使得 EOB是以OB为底边的等腰三角形?如果存在,直接写出所有符合条件的点E的坐标,如果不存在,请说明理由.(4)、在平面直角坐标系xOy中,是否存在一点F,使得以O,A,B,F为顶点的四边形是平行四边形?如果存在,请直接写出所有符合条件的点F的坐标;如果不存在,请说明理由.
(1)、求点A、B、C的坐标;(2)、如图1,若点D是线段OA上的点,且 COD的面积为 ,求直线CD的函数表达式;(3)、在直线OA上,是否存在一点E,使得 EOB是以OB为底边的等腰三角形?如果存在,直接写出所有符合条件的点E的坐标,如果不存在,请说明理由.(4)、在平面直角坐标系xOy中,是否存在一点F,使得以O,A,B,F为顶点的四边形是平行四边形?如果存在,请直接写出所有符合条件的点F的坐标;如果不存在,请说明理由.