河北省沧州市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 化简 的结果是( )A、2 B、4 C、8 D、162. 直线 不经过( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列各组数中能作为直角三角形的三边长的是( )A、1,2,3 B、 , , C、4,5, D、6,8,124. 在函数 中,自变量x的取值范围是( )A、x>2 B、x≤2且x≠0 C、x<2 D、x>2且x≠05. 下列各曲线中,表示y是x的函数的有( )
 A、1个 B、2个 C、3个 D、4个6. 在战“疫”诗歌创作大赛中,有7名同学进入了决赛,他们的最终成绩均不同.小弘同学想知道自己能否进入前3名,除要了解自己的成绩外,还要了解这7名同学成绩的( )A、中位数 B、平均数 C、众数 D、方差7. 已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )A、y=4x(x≥0) B、y=4x﹣3(x≥ ) C、y=3﹣4x(x≥0) D、y=3﹣4x(0≤x≤ )8. 下列命题的逆命题不成立的是( )A、平行四边形的对角线互相平分 B、四个角都是直角的四边形是矩形 C、菱形的对角线互相垂直 D、四条边都相等的四边形是正方形9. 已知直线y=﹣3x+m过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )A、y1>y2 B、y1<y2 C、y1=y2 D、不能确定10. 如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2 . 则OC的长为( )
A、1个 B、2个 C、3个 D、4个6. 在战“疫”诗歌创作大赛中,有7名同学进入了决赛,他们的最终成绩均不同.小弘同学想知道自己能否进入前3名,除要了解自己的成绩外,还要了解这7名同学成绩的( )A、中位数 B、平均数 C、众数 D、方差7. 已知小明从A地到B地,速度为4千米/小时,A、B两地相距3千米,若用x(小时)表示行走的时间,y(千米)表示余下的路程,则y与x之间的函数表达式是( )A、y=4x(x≥0) B、y=4x﹣3(x≥ ) C、y=3﹣4x(x≥0) D、y=3﹣4x(0≤x≤ )8. 下列命题的逆命题不成立的是( )A、平行四边形的对角线互相平分 B、四个角都是直角的四边形是矩形 C、菱形的对角线互相垂直 D、四条边都相等的四边形是正方形9. 已知直线y=﹣3x+m过点A(﹣1,y1)和点(﹣3,y2),则y1和y2的大小关系是( )A、y1>y2 B、y1<y2 C、y1=y2 D、不能确定10. 如图,在∠MON的两边上分别截取OA、OB,使OA=OB;分别以点A、B为圆心,OA长为半径作弧,两弧交于点C;连接AC、BC、AB、OC.若AB=2cm,四边形OACB的面积为4cm2 . 则OC的长为( )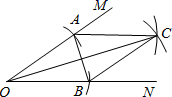 A、2 B、3 C、4 D、511. 船工小王驾驶一艘小艇匀速从甲港向乙港航行,离开甲港后不久便发现有重要物品落在甲港,小王马上驾驶小艇以相同的速度驰回甲港,到达甲港后,因找重要物品耽误了一段时间,为了按时到达乙港,小王回乙港时,加快了航行速度.则小艇离乙港的距离y与时间t之间的函数关系的大致图象是( )A、
A、2 B、3 C、4 D、511. 船工小王驾驶一艘小艇匀速从甲港向乙港航行,离开甲港后不久便发现有重要物品落在甲港,小王马上驾驶小艇以相同的速度驰回甲港,到达甲港后,因找重要物品耽误了一段时间,为了按时到达乙港,小王回乙港时,加快了航行速度.则小艇离乙港的距离y与时间t之间的函数关系的大致图象是( )A、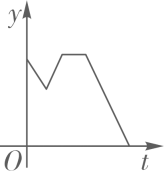 B、
B、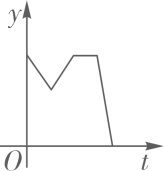 C、
C、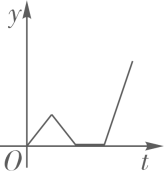 D、
D、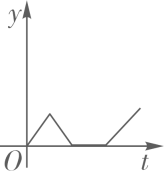 12. 数形结合是数学解题中常用的思想方法,使用数形结合的方法,很多问题可迎刃而解,且解法简洁.如图,直线y=3x和直线y=ax﹣b交于点(1,3),根据图象分析,3x>ax﹣b的解集为( )
12. 数形结合是数学解题中常用的思想方法,使用数形结合的方法,很多问题可迎刃而解,且解法简洁.如图,直线y=3x和直线y=ax﹣b交于点(1,3),根据图象分析,3x>ax﹣b的解集为( )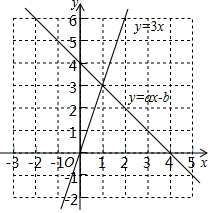 A、x>1 B、x<1 C、x>3 D、x<013. 《九章算术》是我国古代一部著名的数学专著,其中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子(1丈=10尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺.问折断处高地面的距离为( )A、5.45尺 B、4.55尺 C、5.8尺 D、4.2尺14. 某班有50人,一次体能测试后,符老师对测试成绩进行了统计.因小芝没有参加本次集体测试,因此计算其他49人的平均分为90分,方差s2=39.后来小芝进行了补测,成绩为90分,关于该班50人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变15. 如图,在 中, ,点 分别是边 的中点,延长 至 ,使 , 若 ,则EF的长是( )
A、x>1 B、x<1 C、x>3 D、x<013. 《九章算术》是我国古代一部著名的数学专著,其中记载了一个“折竹抵地”问题:今有竹高一丈,末折抵地,去本三尺,问折者高几何?其意思是:有一根与地面垂直且高一丈的竹子(1丈=10尺),现被大风折断成两截,尖端落在地面上,竹尖与竹根的距离为三尺.问折断处高地面的距离为( )A、5.45尺 B、4.55尺 C、5.8尺 D、4.2尺14. 某班有50人,一次体能测试后,符老师对测试成绩进行了统计.因小芝没有参加本次集体测试,因此计算其他49人的平均分为90分,方差s2=39.后来小芝进行了补测,成绩为90分,关于该班50人的测试成绩,下列说法正确的是( )A、平均分不变,方差变大 B、平均分不变,方差变小 C、平均分和方差都不变 D、平均分和方差都改变15. 如图,在 中, ,点 分别是边 的中点,延长 至 ,使 , 若 ,则EF的长是( ) A、7 B、6 C、5 D、416. 有一个边长为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( )
A、7 B、6 C、5 D、416. 有一个边长为1的正方形,经过一次“生长”后,在他的左右肩上生出两个小正方形,其中,三个正方形围成的三角形是直角三角形,再经过一次“生长”后,变成了如图,如果继续“生长”下去,它将变得“枝繁叶茂”,请你算出“生长”了2021次后形成的图形中所有的正方形的面积和是( ) A、2022 B、2021 C、2020 D、1
A、2022 B、2021 C、2020 D、1二、填空题
-
17. 一组数据4、5、8、x、3的平均数是5,则这组数的众数是 .18. 如果最简二次根式 与 可以合并,则x= .19. 我们规定:当k,b为常数,k≠0,b≠0,k≠b时,一次函数y=kx+b与y=bx+k互为交换函数,例如:y=5x+2的交换函数为y=2x+5.一次函数y=kx+2与它的交换函数图象的交点横坐标为 .20. 如图,在四边形ABCD中,AD∥BC,AD=9cm,BC=6cm,点P在AD边上以每秒2cm的速度从点A向点D运动,点Q在BC边上,以每秒1cm的速度从点C向点B运动,当秒时,直线PQ在四边形ABCD内部能截出一个平行四边形.

三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 如图,正方形网格的每个小方格都是边长为1的正方形,每个小正方形的顶点叫格点.某数学探究小组进行了如下探究活动:以格点为顶点分别按下列要求画图形.
 (1)、画一个三角形、使三边长为3, , 在网格1中完成;(2)、画一个平行四边形,使其有一锐角为45°,且面积为6,在网格2中完成;(3)、线段AB的端点都在格点上,将线段AB平移得到线段CD,并保证点C和点D也在格点上.
(1)、画一个三角形、使三边长为3, , 在网格1中完成;(2)、画一个平行四边形,使其有一锐角为45°,且面积为6,在网格2中完成;(3)、线段AB的端点都在格点上,将线段AB平移得到线段CD,并保证点C和点D也在格点上.①平移后使形成的四边形ABDC为正方形,画出符合条件的所有图形,在网格3中完成;
②平移后使形成的四边形ABDC为菱形(正方形除外),画出符合条件的所有图形,在网格4中完成.
23. 九年级甲班和乙班各推选10名同学进行投篮比赛,按照比赛规则,每人各投了10个球;将两班选手的进球数绘制成如下尚不完整的统计图表:进球数/个
10
9
8
7
4
3
乙班人数/个
1
1
2
4
1
1
平均成绩
中位数
众数
甲班
7
7
c
乙班
a
b
7
 (1)、表格中b= , c= 并求a的值;(2)、如果要从这两个班中选出一个成绩较为稳定的班代表年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班,请说明理由;如果要争取个人进球数进入学校前三名,你认为应该选择哪个班,请说明理由.24. “莓好生活,幸福家园”2021年草莓旅游文化节期间,甲、乙两家草莓采摘园草莓品质相同,销售价格也相同,且推出了优惠方案:
(1)、表格中b= , c= 并求a的值;(2)、如果要从这两个班中选出一个成绩较为稳定的班代表年级参加学校的投篮比赛,争取夺得总进球数团体第一名,你认为应该选择哪个班,请说明理由;如果要争取个人进球数进入学校前三名,你认为应该选择哪个班,请说明理由.24. “莓好生活,幸福家园”2021年草莓旅游文化节期间,甲、乙两家草莓采摘园草莓品质相同,销售价格也相同,且推出了优惠方案:甲园
甲园游客进园需购买门票,采摘的草莓六折优惠
乙园
乙园游客进园不需购买门票,采摘的草莓超过一定数量后,超过部分打折优惠
优惠期间,某游客的草莓采摘量为x(千克),在甲园所需总费用为y甲(元),在乙园所需费用为y乙(元),y甲、y乙与x之间的函数关系如图所示.
 (1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克元;(2)、当x>10时,求y乙与x的函数表达式;(3)、当游客采摘22千克草莓时,选择哪一家采摘园更便宜?25. 如图,在平行四边形ABCD中,BC=AC,E、F分别是AB、CD的中点,连接CE、AF.
(1)、甲采摘园的门票是元,两个采摘园优惠前的草莓单价是每千克元;(2)、当x>10时,求y乙与x的函数表达式;(3)、当游客采摘22千克草莓时,选择哪一家采摘园更便宜?25. 如图,在平行四边形ABCD中,BC=AC,E、F分别是AB、CD的中点,连接CE、AF. (1)、求证:四边形AECF是矩形;(2)、当平行四边形ABCD的边或角满足什么关系时,四边形AECF是正方形?请说明理由.(3)、在(2)的条件下,若AE=4,点M为EC中点,当点P在线段AC上运动时,求PE+PM的最小值.26. 在一次函数学习中,我们经历了列表、描点、连线画函数图象,结合图象研究函数性质并对其性质进行应用的过程.小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.请同学们阅读探究过程并解答:
(1)、求证:四边形AECF是矩形;(2)、当平行四边形ABCD的边或角满足什么关系时,四边形AECF是正方形?请说明理由.(3)、在(2)的条件下,若AE=4,点M为EC中点,当点P在线段AC上运动时,求PE+PM的最小值.26. 在一次函数学习中,我们经历了列表、描点、连线画函数图象,结合图象研究函数性质并对其性质进行应用的过程.小华根据学习函数的经验,对函数y=|x|﹣2的图象与性质进行了探究.请同学们阅读探究过程并解答: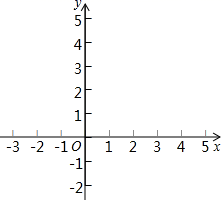
在函数y=|x|﹣2中,自变量x可以是任意实数;
(1)、下表是y与x的几组对应值.x
…
﹣3
﹣2
﹣1
0
1
2
3
…
y
…
1
0
﹣1
﹣2
﹣1
0
m
…
①m=;
②若A(n,8),B(10,8)为该函数图象上不同的两点,则n=;
(2)、在平面直角坐标系xOy中,描出表中各组对应值为坐标的点.并根据描出的点,画出该函数的图象;根据函数图象可得:①当x=时,y有最小值为;
②如果y=|x|﹣2的图象与直线y=k有两个交点,则k的取值范围是;
③请再写出该函数的一条性质:;
(3)、已知直线y1= x,①求它与函数y=|x|﹣2的图象围成的三角形的面积;
②直接写出当y1<y时,x的取值范围.