河北省保定市曲阳县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 函数 的自变量x的取值范围是( )A、 B、 C、 D、2. 国务院决定于2020年11月1日零时开展第七次全国人口普查,人口调查采用普查方式的理由是( )A、人口调查的数目不太大 B、人口调查需要获得全面准确的信息 C、人口调查具有破坏性 D、受条件限制,无法进行抽样调查3. 下列角度中,是多边形内角和的只有( )A、270° B、560° C、630° D、1 800°4. 经过两点A(2,3)、B(-4,3)作直线AB,则直线AB( )A、平行于x轴 B、平行于y轴 C、经过原点 D、无法确定5. 一次函数y=kx-(2-b)的图像如图所示,则k和b的取值范围是( )
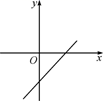 A、k>0,b>2 B、k>0,b<2 C、k<0,b>2 D、k<0,b<26. 如图,在矩形ABCD中,有以下结论:①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.正确结论的个数是( )
A、k>0,b>2 B、k>0,b<2 C、k<0,b>2 D、k<0,b<26. 如图,在矩形ABCD中,有以下结论:①△AOB是等腰三角形;②S△ABO=S△ADO;③AC=BD;④AC⊥BD;⑤当∠ABD=45°时,矩形ABCD会变成正方形.正确结论的个数是( )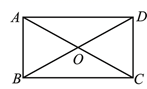 A、2 B、3 C、4 D、57. 如图,在平面直角坐标系中,点 在第一象限,若点 关于 轴的对称点 在直线 上,则 的值为( )
A、2 B、3 C、4 D、57. 如图,在平面直角坐标系中,点 在第一象限,若点 关于 轴的对称点 在直线 上,则 的值为( ) A、-1 B、1 C、2 D、38. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )
A、-1 B、1 C、2 D、38. 如图,将正方形OABC放在平面直角坐标系中,O是原点,点A的坐标为(1, ),则点C的坐标为( )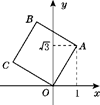 A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)9. 如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( )
A、(- ,1) B、(-1, ) C、( ,1) D、(- ,-1)9. 如图1,平行四边形纸片ABCD的面积为120,AD=20,AB=18.今沿两对角线将四边形ABCD剪成甲、乙、丙、丁四个三角形纸片.若将甲、丙合并(AD、CB重合)形成一线对称图形戊,如图2所示,则图形戊的两对角线长度和( ) A、26 B、29 C、24 D、2510.
A、26 B、29 C、24 D、2510.如图是本地区一种产品30天的销售图象,图①是产品日销售量y(单位:件)与时间t(单位;天)的函数关系,图②是一件产品的销售利润z(单位:元)与时间t(单位:天)的函数关系,已知日销售利润=日销售量×一件产品的销售利润,下列结论错误的是( )
 A、第24天的销售量为200件 B、第10天销售一件产品的利润是15元 C、第12天与第30天这两天的日销售利润相等 D、第30天的日销售利润是750元
A、第24天的销售量为200件 B、第10天销售一件产品的利润是15元 C、第12天与第30天这两天的日销售利润相等 D、第30天的日销售利润是750元二、填空题
-
11. 期末考试后,小红将本班50名学生的数学成绩进行分类统计,得到如图的扇形统计图,则优生人数为 .
 12. 如图,在△ABC中,AB=5,BC=7,EF是△ABC的中位线,则EF的长度范围是 .
12. 如图,在△ABC中,AB=5,BC=7,EF是△ABC的中位线,则EF的长度范围是 . 13. 已知 ABC的边BC在x轴上,顶点A在y轴上,且B点坐标为(﹣6,0),C点坐标为(2,0), ABC的面积为12,则A点坐标为 .14. 变量x与y之间的关系y= x2﹣2,当自变量x=2时,因变量y的值是 .15. 如图,已知菱形ABCD中,∠ABD=70°,则∠ABC= .
13. 已知 ABC的边BC在x轴上,顶点A在y轴上,且B点坐标为(﹣6,0),C点坐标为(2,0), ABC的面积为12,则A点坐标为 .14. 变量x与y之间的关系y= x2﹣2,当自变量x=2时,因变量y的值是 .15. 如图,已知菱形ABCD中,∠ABD=70°,则∠ABC= .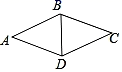 16. 某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是打 折.
16. 某商店在节日期间开展优惠促销活动:购买原价超过500元的商品,超过500元的部分可以享受打折优惠.若购买商品的实际付款金额y(单位:元)与商品原价x(单位:元)的函数关系的图象如图所示,则超过500元的部分可以享受的优惠是打 折. 17. 在一个凸n边形的纸板上切下一个三角形后,剩下一个内角和为1080°的多边形,则n的值为 .18. 在平面直角坐标系中,方程2x+3y=4所对应的直线为a,方程3x+2y=4所对应的直线为b,直线a与b的交点坐标为 .19. 如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论:①BO=OH;②DF=CE;③DH=CG;④AB=AE;正确的是 . (填序号)
17. 在一个凸n边形的纸板上切下一个三角形后,剩下一个内角和为1080°的多边形,则n的值为 .18. 在平面直角坐标系中,方程2x+3y=4所对应的直线为a,方程3x+2y=4所对应的直线为b,直线a与b的交点坐标为 .19. 如图,在▱ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连接BE,下列结论:①BO=OH;②DF=CE;③DH=CG;④AB=AE;正确的是 . (填序号) 20. A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线 所示.其中点C的坐标是 ,点D的坐标是 ,则点E的坐标是 .
20. A,B两地相距240 km,甲货车从A地以40km/h的速度匀速前往B地,到达B地后停止,在甲出发的同时,乙货车从B地沿同一公路匀速前往A地,到达A地后停止,两车之间的路程y(km)与甲货车出发时间x(h)之间的函数关系如图中的折线 所示.其中点C的坐标是 ,点D的坐标是 ,则点E的坐标是 .
三、解答题
-
21. 如图,在平行四边形ABCD中,对角线AC,BD相交于点O,分别过点A,C作 , ,垂足分别为E,F.AC平分 .
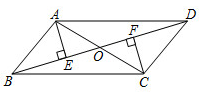 (1)、若 ,求 的度数;(2)、求证: .22. 如图,在平面直角坐标系 中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形 的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动).
(1)、若 ,求 的度数;(2)、求证: .22. 如图,在平面直角坐标系 中,A(4,0),C(0,6),点B在第一象限内,点P从原点O出发,以每秒2个单位长度的速度沿着长方形 的边逆时针移动一周(即:沿着O→A→B→C→O的路线移动). (1)、点B的坐标为;(2)、当点P移动4s时,求出点P的坐标;(3)、在移动过程中,当点P到 轴的距离为5个单位长度时,求点P移动的时间t .23. 某校七年级共有500名学生,团委准备调查他们对“低碳”知识的了解程度,
(1)、点B的坐标为;(2)、当点P移动4s时,求出点P的坐标;(3)、在移动过程中,当点P到 轴的距离为5个单位长度时,求点P移动的时间t .23. 某校七年级共有500名学生,团委准备调查他们对“低碳”知识的了解程度, (1)、在确定调查方式时,团委设计了以下三种方案:
(1)、在确定调查方式时,团委设计了以下三种方案:方案一:调查七年级部分女生;
方案二:调查七年级部分男生;
方案三:到七年级每个班去随机调查一定数量的学生
请问其中最具有代表性的一个方案是
(2)、团委采用了最具有代表性的调查方案,并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示),请你根据图中信息,将其补充完整;(3)、请你估计该校七年级约有多少名学生比较了解“低碳”知识.24. 如图,直线 与 轴交于点 ,直线 与 轴交于点 ,两条直线交于点 . (1)、方程组 的解是;(2)、当 与 同时成立时, 的取值范围是;(3)、求 的面积;(4)、在直线 的图象上存在异于点 的另一点 ,使得 与 的面积相等,请求出点 的坐标.25. 甲、乙两人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度v1与v2(v1>v2),甲前一半的路程使用速度v1、后一半的路程使用速度v2;乙前一半的时间使用速度v2、后一半的时间使用速度v1 .
(1)、方程组 的解是;(2)、当 与 同时成立时, 的取值范围是;(3)、求 的面积;(4)、在直线 的图象上存在异于点 的另一点 ,使得 与 的面积相等,请求出点 的坐标.25. 甲、乙两人同时从A地出发,沿同一条道路去B地,途中都使用两种不同的速度v1与v2(v1>v2),甲前一半的路程使用速度v1、后一半的路程使用速度v2;乙前一半的时间使用速度v2、后一半的时间使用速度v1 . (1)、甲、乙两人从A地到达B地的平均速度各是多少(用v1和v2表示)(2)、甲、乙两人谁先到达B地,为什么?(3)、如图是甲从A地到达B地的路程s与时间t的函数图象,请你在图中画出相应的乙从A地到达B地的路程s与t的函数图象.26. 已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:
(1)、甲、乙两人从A地到达B地的平均速度各是多少(用v1和v2表示)(2)、甲、乙两人谁先到达B地,为什么?(3)、如图是甲从A地到达B地的路程s与时间t的函数图象,请你在图中画出相应的乙从A地到达B地的路程s与t的函数图象.26. 已知在Rt△ABC中,∠ACB=90°,现按如下步骤作图:①分别以A,C为圆心,a为半径(a> AC)作弧,两弧分别交于M,N两点;
②过M,N两点作直线MN交AB于点D,交AC于点E;
③将△ADE绕点E顺时针旋转180°,设点D的像为点F.
 (1)、请在图中直线标出点F并连接CF;(2)、求证:四边形BCFD是平行四边形;(3)、当∠B为多少度时,四边形BCFD是菱形.
(1)、请在图中直线标出点F并连接CF;(2)、求证:四边形BCFD是平行四边形;(3)、当∠B为多少度时,四边形BCFD是菱形.