广东省肇庆市广宁县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
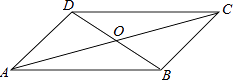
1. 要使 有意义,则x的取值范围为(( )A、x≤0 B、x≥1 C、x≥0 D、x≤12. 下列各组数据中的三个数作为三角形的边长,其中能构成直角三角形的是( )A、 , , B、1, , C、6,7,8 D、2,3,43. 下列二次根式是最简二次根式的是( )A、 B、 C、 D、4. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )
 A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC5. 下列事件中是必然事件是( )A、明天太阳从西边升起 B、篮球队员在罚球线投篮一次,未投中 C、实心铁球投入水中会沉入水底 D、抛出一枚硬币,落地后正面向上6. 两个一次函数y=ax+b和y=bx+a在同一直角坐标系中的图象可能是( )A、
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC5. 下列事件中是必然事件是( )A、明天太阳从西边升起 B、篮球队员在罚球线投篮一次,未投中 C、实心铁球投入水中会沉入水底 D、抛出一枚硬币,落地后正面向上6. 两个一次函数y=ax+b和y=bx+a在同一直角坐标系中的图象可能是( )A、 B、
B、 C、
C、 D、
D、 7. 下列命题中,是真命题的是()A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形8. 学校决定从甲、乙两人中选一人去参加全县的射击比赛,在最后5次射击训练中,甲、乙两人的射击成绩分别为(单位:环)
7. 下列命题中,是真命题的是()A、两条对角线互相平分的四边形是平行四边形 B、两条对角线相等的四边形是矩形 C、两条对角线互相垂直的四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形8. 学校决定从甲、乙两人中选一人去参加全县的射击比赛,在最后5次射击训练中,甲、乙两人的射击成绩分别为(单位:环)甲:10 9 10 8 8
乙:7 9 10 10 9
则选谁去参加比赛更合适( )
A、甲、乙选谁都一样 B、选甲 C、选乙 D、无法确定9. 对于函数y=﹣4x+3,下列结论正确的是( )A、它的图象必经过点(﹣1,1) B、y随x的增大而增大 C、当x>0时,y>0 D、它的图象不经过第三象限10. 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=1,CE=3,H是AF的中点,那么CH的长是( )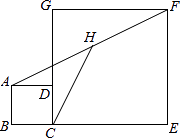 A、2.5 B、 C、 D、2
A、2.5 B、 C、 D、2二、填空题
-
11. 一组数据为2,3,3,5,7,则这组数据的中位数是 .12. 计算 .13. 如图,一个圆形转盘被分成6个圆心角都是60°的扇形.任意转动这个转盘1次,当转动停止时,指针指向阴影区域的概率为 .
 14. 已知某校女子田径队23人年龄的平均数是13岁,但是后来发现其中一位同学的年龄登记出现不符合题意,将14岁写成了15岁,经重新计算后,正确的平均数为a岁,则a13(在横线上填上“>”或“=”或“<”).15. 如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的点,ED平分∠AEC,则EC= .
14. 已知某校女子田径队23人年龄的平均数是13岁,但是后来发现其中一位同学的年龄登记出现不符合题意,将14岁写成了15岁,经重新计算后,正确的平均数为a岁,则a13(在横线上填上“>”或“=”或“<”).15. 如图,在矩形ABCD中,AD=10,AB=6,点E为BC上的点,ED平分∠AEC,则EC= . 16. 若函数y=(k+1)x+k2-1是正比例函数,则k的值为。17. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF.正确的是 .
16. 若函数y=(k+1)x+k2-1是正比例函数,则k的值为。17. 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF.正确的是 .
三、解答题
-
18. 计算: .19. 如图,一棵大树被大风刮断后,折断处离地面 ,树的顶端离树根 ,则这棵树在折断之前的高度是多少米?
 20. 如图,▱ABCD的对角线AC,BD相交于O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF.
20. 如图,▱ABCD的对角线AC,BD相交于O,EF过点O且与AD,BC分别相交于点E,F.求证:OE=OF. 21. 如图,在四边形 中, .求
21. 如图,在四边形 中, .求 (1)、 的度数;(2)、四边形 的面积.22. 某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):
(1)、 的度数;(2)、四边形 的面积.22. 某中学开设的体育选修课有篮球、足球、排球、羽毛球、乒乓球,学生可以根据自己的爱好选修其中1门.某班班主任对全班同学的选课情况进行了调查统计,制成了两幅不完整的统计图(图(1)和图(2)):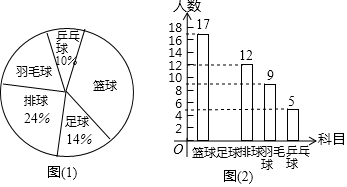 (1)、请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);(2)、在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?23. 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.
(1)、请你求出该班的总人数,并补全条形图(注:在所补小矩形上方标出人数);(2)、在该班团支部4人中,有1人选修排球,2人选修羽毛球,1人选修乒乓球.如果该班班主任要从他们4人中任选2人作为学生会候选人,那么选出的两人中恰好有1人选修排球、1人选修羽毛球的概率是多少?23. 如图,BD是△ABC的角平分线,点E,F分别在BC,AB上,且DE∥AB,BE=AF.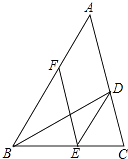 (1)、求证:四边形ADEF是平行四边形;(2)、若∠ABC=60°,BD=4,求平行四边形ADEF的面积.24. 如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
(1)、求证:四边形ADEF是平行四边形;(2)、若∠ABC=60°,BD=4,求平行四边形ADEF的面积.24. 如图,直线l1的函数解析式为y=﹣2x+4,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C. (1)、求直线l2的函数解析式;(2)、求△ADC的面积;
(1)、求直线l2的函数解析式;(2)、求△ADC的面积;
(3)、在直线l2上是否存在点P,使得△ADP面积是△ADC面积的2倍?如果存在,请求出P坐标;如果不存在,请说明理由.25. 如图,把矩形OABC放入平面直角坐标系xO中,使OA、OC分别落在x、y轴的正半轴上,其中AB=15,对角线AC所在直线解析式为y=﹣ x+b,将矩形OABC沿着BE折叠,使点A落在边OC上的点D处. (1)、求点B的坐标;(2)、求EA的长度;(3)、点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.
(1)、求点B的坐标;(2)、求EA的长度;(3)、点P是y轴上一动点,是否存在点P使得△PBE的周长最小,若存在,请求出点P的坐标,若不存在,请说明理由.