广东省惠州市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 下列二次根式,最简二次根式是( )A、 B、 C、 D、2. 下列几组数中,不能作为直角三角形三边长度的是( )A、3,4,5 B、5,7,8 C、8,15,17 D、1,3. 在函数y= 中,自变量x的取值范围是( )A、x≥2 B、x≥﹣2 C、x>2 D、x>﹣24. 下列图象中,表示 不是 的函数的是( )A、
 B、
B、 C、
C、 D、
D、 5. 若一次函数y=x+4的图象上有两点A(﹣ ,y1)、B(1,y2),则下列说法正确的是( )A、y1>y2 B、y1≥y2 C、y1<y2 D、y1≤y26. 下列计算结果,正确的是( )A、 = B、3 =3、 C、 × = D、 =7. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB,若AD=4, ,则AB的长为( )
5. 若一次函数y=x+4的图象上有两点A(﹣ ,y1)、B(1,y2),则下列说法正确的是( )A、y1>y2 B、y1≥y2 C、y1<y2 D、y1≤y26. 下列计算结果,正确的是( )A、 = B、3 =3、 C、 × = D、 =7. 如图,在平行四边形ABCD中,对角线AC、BD相交于点O,且OA=OB,若AD=4, ,则AB的长为( ) A、 B、 C、8 D、8. 一组数据3、2、4、5、2,则这组数据的众数是( )A、2 B、3 C、3.2 D、49. 对于函数 ,下列结论正确的是( )A、它的图象必经过点(-1,1) B、它的图象不经过第三象限 C、当 时, D、 的值随 值的增大而增大10. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )
A、 B、 C、8 D、8. 一组数据3、2、4、5、2,则这组数据的众数是( )A、2 B、3 C、3.2 D、49. 对于函数 ,下列结论正确的是( )A、它的图象必经过点(-1,1) B、它的图象不经过第三象限 C、当 时, D、 的值随 值的增大而增大10. 小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,看作一个容器.然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出容器最高水位h与注水时间t之间的变化情况的是( )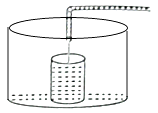 A、
A、 B、
B、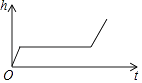 C、
C、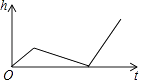 D、
D、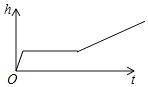
二、填空题
-
11. 化为最简二次根式 .12. 如图,¨ABCD的对角线AC,BD交于点O,M是CD的中点,连接OM,若OM=2,则BC的长是 .
 13. 菱形的对角线长分别为6和8,则此菱形的面积为 .14. 甲、乙两个样本,甲的方差为0.102,乙的方差为0.06,哪个样本的数据波动大?答: .15. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为 .
13. 菱形的对角线长分别为6和8,则此菱形的面积为 .14. 甲、乙两个样本,甲的方差为0.102,乙的方差为0.06,哪个样本的数据波动大?答: .15. 如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为PQ,则线段BQ的长度为 . 16. 实数 、 在数轴上位置如图,化简: ;
16. 实数 、 在数轴上位置如图,化简: ;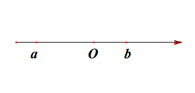 17. 如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1 , 再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是 .
17. 如图,正方形ABCD的边长为2,顺次连接正方形ABCD四边的中点得到第一个正方形A1B1C1D1 , 再顺次连接正方形A1B1C1D1四边的中点得到第二个正方形A2B2C2D2…,以此类推,则第五个正方形A5B5C5D5周长是 .
三、解答题
-
18. 计算: .19. 已知y与x成正比例,且x=2时,y=﹣6.求:y与x的函数解析式.20. 如图四边形ABCD是一块草坪,量得四边长AB=3m,BC=4m,DC=12m,AD=13m,∠B=90°,求这块草坪的面积.
 21. 已知 , ,计算:(1)、(2)、22. 珠海市某中学在创建“书香校园”活动中,为了解学生的读书情况,某校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题:
21. 已知 , ,计算:(1)、(2)、22. 珠海市某中学在创建“书香校园”活动中,为了解学生的读书情况,某校抽样调查了部分同学在一周内的阅读时间,绘制如下统计图.根据图中信息,解答下列问题: (1)、被抽查学生阅读时间的中位数为h,平均数为h;(2)、若该校共有1500名学生,请你估算该校一周内阅读时间不少于3h的学生人数.23. 如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.
(1)、被抽查学生阅读时间的中位数为h,平均数为h;(2)、若该校共有1500名学生,请你估算该校一周内阅读时间不少于3h的学生人数.23. 如图,在正方形ABCD中,AF=BE,AE与DF相交于点O.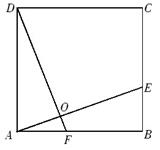 (1)、求证:△DAF≌△ABE;(2)、写出线段AE、DF的数量和位置关系,并说明理由.24. 如图,已知函数y=mx 的图象为直线l1 , 函数y=kx+b的图象为直线l2 , 直线l1、l2分别交x轴于点B和点C(3,0),分别交y轴于点D和E,l1和l2相交于点A(2,2).
(1)、求证:△DAF≌△ABE;(2)、写出线段AE、DF的数量和位置关系,并说明理由.24. 如图,已知函数y=mx 的图象为直线l1 , 函数y=kx+b的图象为直线l2 , 直线l1、l2分别交x轴于点B和点C(3,0),分别交y轴于点D和E,l1和l2相交于点A(2,2). (1)、填空:m=;求直线l2的解析式为;(2)、若点M是x轴上一点,连接AM,当△ABM的面积是△ACM面积的2倍时,请求出符合条件的点M的坐标;(3)、若函数y=nx﹣6的图象是直线l3 , 且l1、l2、l3不能围成三角形,直接写出n的值.25. 如图,矩形ABCD的对角线AC,BD相交于点O,将△COD沿CD所在直线折叠,得到△CED.
(1)、填空:m=;求直线l2的解析式为;(2)、若点M是x轴上一点,连接AM,当△ABM的面积是△ACM面积的2倍时,请求出符合条件的点M的坐标;(3)、若函数y=nx﹣6的图象是直线l3 , 且l1、l2、l3不能围成三角形,直接写出n的值.25. 如图,矩形ABCD的对角线AC,BD相交于点O,将△COD沿CD所在直线折叠,得到△CED. (1)、求证:四边形OCED是菱形;(2)、若AB=2,当四边形OCED是正方形时,求OC的长;(3)、若BD=3,∠ACD=30°,P是CD边上的动点,Q是CE边上的动点,求PE+PQ的最小值.
(1)、求证:四边形OCED是菱形;(2)、若AB=2,当四边形OCED是正方形时,求OC的长;(3)、若BD=3,∠ACD=30°,P是CD边上的动点,Q是CE边上的动点,求PE+PQ的最小值.