广东省佛山市顺德区2020-2021学年八年级下学期数学期末试卷

试卷更新日期：2021-09-02 类型：期末考试

进入出卷网下载

一、单选题

1. 垃圾分类就是将垃圾分门别类地投放，并通过分类地清运和回收使之重新变成资源．对于下列垃圾分类的标志，既是轴对称图形，又是中心对称图形的是（）

A、有害垃圾 B、厨余垃圾 C、可回收物 D、其它垃圾

查看试题解析
2. 若等腰三角形的顶角是40°，则它的底角是（）

A、40° B、70° C、80° D、100°

查看试题解析
3. 若分式 $\frac{8}{x - 1}$ 有意义，则x的取值范围是（）

A、x=1 B、x≠1 C、x>1 D、x<1

查看试题解析
4. 一个多边形的内角和是720°，这个多边形是（）

A、五边形 B、六边形 C、七边形 D、八边形

查看试题解析
5. 如图，▱ABCD中，AB=3，BC=5，AE平分∠BAD交BC于点E，则CE的长为（）

A、1 B、2 C、3 D、4

查看试题解析
6. 下列因式分解正确的是（）

A、（x+y）（x﹣y）＝x²﹣y² B、x²﹣y²＝（x+y）（x﹣y） C、（x+y）²＝x²+y² D、x²+y²＝（x+y）²

查看试题解析
7. 一次函数 $y = k x + b$ 的图象如图所示，则不等式 $k x + b < 0$ 的解集是（）

A、 $x > - 2$ B、 $x < - 2$ C、 $x < - 3$ D、 $x > - 3$

查看试题解析
8. 如图，若正方形ABCD绕图中某点顺时针旋转90°得到正方形EFGH，则旋转中心应是（）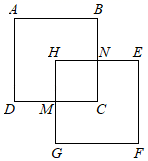

A、H点 B、N点 C、C点 D、M点

查看试题解析
9. 下面所描述的两个等腰三角形不一定全等的是（）

A、顶角和底角分别相等 B、腰和底角分别相等 C、底角和底边分别相等 D、腰和底边分别相等

查看试题解析
10. 如图，l₁反映了某产品的销售收入（单位：元）与销售量（单位：t）之间的关系，l₂反映了该产品的销售成本（单位：元）与销售量之间的关系，当销售收入大于销售成本时，该产品才开始赢利．下列说法错误的是（）

A、当销售量为0t时，销售收入为0元 B、当销售量小于4t时，没有赢利 C、当销售量为6t时，赢利1000元 D、当赢利为4000元，销售量为10t

查看试题解析

二、填空题

11. x的3倍小于6，用不等式表示为．

查看试题解析
12. 因式分解：2a²﹣2= ．

查看试题解析
13. 在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝6cm，则BC＝cm.

查看试题解析
14. 若▱ABCD中，∠A=50°，则∠C=°．

查看试题解析
15. 计算： $\frac{3 a}{4 y} \cdot \frac{2 y^{2}}{3 a^{2}}$ ＝．

查看试题解析
16. 若等腰三角形的两边分别为12和10，则等腰三角形底边上的高为．

查看试题解析
17. 在等腰三角形ABC中，AB＝AC，AC边上的中垂线交BC边于点D，垂足为E点，∠ABC的平分线交AC边于点F，交DE于点G，连接AD交BF于点H．则下列结论正确的是．
①C_△ABD＝AC+BC（C表示周长）；

②AH＝DH；

③若AB＝DB，则∠C＝36°；

④若BD＝CD，则图中有6个等腰三角形；

⑤若∠BDE＝α，则∠BAC＝360°﹣2α．

查看试题解析

三、解答题

18. 解不等式组： ${\begin{array}{l} - 2 x < 4 \\ \frac{3 x - 1}{2} < 1 + x \end{array}$ ．

查看试题解析
19. 先化简，后求值： $(1 - \frac{x^{2} + 4}{x^{2} + 4 x + 4}) \div \frac{x}{x + 2}$ ，其中x＝ $\sqrt{2}$ ﹣2．

查看试题解析
20. △ABC如图所示．

(1)、利用尺规作图法作▱ABCD（保留作图痕迹，不用写作法）；

(2)、在（1）所作的▱ABCD中，连接BD．若∠BAC＝90°，AB＝3，AC＝8，求BD的长．

查看试题解析
21. 在平面直角坐标系中，△ABC三个顶点的坐标分别是A（﹣5，1）、B（﹣3，3），C（﹣2，2）．

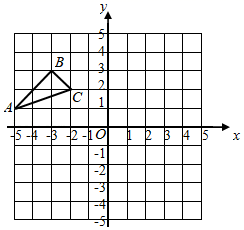(1)、将△ABC平移，使点B的对应点B坐标为（3，4），画出平移后的△A′B′C′，此时平移的距离为；

(2)、求△A′B'C′的面积．

查看试题解析
22. 如图，在△ABC中，中线BE、CD相交于点O．

(1)、若M、N分别是OB、OC的中点，求证：四边形MNED是平行四边形；

(2)、若AB＝AC，求证：△OBC是等腰三角形．

查看试题解析
23. 某市从今年1月1日起调整居民用水价格，每立方米水费上涨20%．小明家去年12月份的水费是50元，而今年6月份的水费则是72元．已知小明家今年6月份的用水量比去年12月份的用水量多了5m³ ．

(1)、求今年居民用水的价格；

(2)、随着夏季高温到来，小明家7月份用水量至少比6月份增加20%．若小明家计划将7月份的水费控制在100元以内，则按计划小明家7月份最多可用水多少立方米？（结果精确到1m³）

查看试题解析
24. 已知函数y₁＝﹣x+3，y₂＝2x﹣4．

(1)、若y₁＜y₂ ，求x的取值范围；

(2)、若点P（m，n）是函数y₁与y₂图象的交点，求32m²+16mn+2n²的值；

(3)、若关于x的不等式组 ${\begin{matrix} y_{1} + 2 b < 0 \\ a - y_{2} > 3 \end{matrix}$ 的解集为﹣1＜x＜1．求（a+1）（b﹣1）的值．

查看试题解析
25. 如图，ABCD的顶点A、B、D的坐标分别（0，0）、（5，0）、（1，3），将▱ABCD绕点A逆时针旋转．

(1)、直接写出点C的坐标；

(2)、如图1，当线段AB′与线段CD有交点时，求点B′的横坐标m的取值范围；

(3)、如图2，当点C′在射线AD上时，在直线AD′上求一点P，使得△AC′P为等腰三角形．

查看试题解析