广东省东莞市2020-2021学年八年级下学期数学期末试卷
试卷更新日期：2021-09-02 类型：期末考试
一、单选题
-
1. 等于（ ）A、2 B、±2 C、﹣2 D、±42. 下列二次根式是最简二次根式的是（ ）A、 B、 C、 D、3. 点A（1，m）在y=2x的图象上，则m的值是（ ）A、1 B、2 C、 D、04. 如图，点P是平面直角坐标系中一点，则点P到原点O的距离是（ ）
A、1 B、2 C、 D、5. 有一组数据：2，5，3，7，5，这组数据的中位数是（ ）A、2 B、3 C、5 D、76. 如图，在▱ABCD中，∠A＋∠C＝140°，则∠B的度数为（ ）
A、140° B、110° C、70° D、无法确定7. 下列计算正确的是（ ）A、 ＋ ＝ B、3＋ ＝3 C、3 ﹣ ＝3 D、（ ＋ ）2＝5＋28. 在一次古诗词诵读比赛中，五位评委给某选手打分，得到互不相等的五个分数，若去掉一个最高分，平均分为a；若去掉一个最低分，平均分为c；同时去掉一个最高分和一个最低分，平均分为m．则a，c，m的大小关系正确的是（ ）A、c＞m＞a B、a＞m＞c C、c＞a＞m D、m＞c＞a9. 如图，Rt△ABC中，∠ACB＝90°，以Rt△ABC的三边为边向外作正方形，其面积分别为S1 ， S2 ， S3 ， 且，且S1＝4，S3＝16，则S2＝（ ）
A、20 B、12 C、2 D、210. 如图，正方形硬纸片ABCD的边长是4，点E，F分别是AB，BC的中点，若沿左图中的虚线剪开，拼成如图的一座“小别墅”，则图中阴影部分的面积是（ ）
A、2 B、4 C、8 D、10二、填空题
-
11. 化简： ＝ ．12. 若二次根式 有意义，则 的取值范围是.13. 一次函数y＝（k﹣1）x＋1中，y随x增大而减小，则k的取值范围是 ．14. 已知矩形的面积为S，相邻两边长分别为a，b，若S＝ ，a＝ ，则b＝ ．15. 如图，矩形ABCD中，对角线AC、BD相交于点O，若OB＝2，∠ACB＝30°，则AB的长度为 ．
16. 如图，直线y＝ax+b过点A（0，2）和点B（﹣3，0），则方程ax+b＝0的解是 ．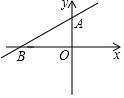
17. 如图1，在菱形ABCD中，动点P从点C出发，沿C→A→D运动至终点D．设点P的运动路程为x，△BCP的面积为y，若y与x的函数图象如图2所示，则图中a的值为 ．
三、解答题
-
18. 计算： ＋ （ ﹣2）﹣（ ）219. 如图，△ABC是等边三角形，边长是6
(1)、求高AD的长；(2)、求△ABC的面积．20. 如图，▱ABCD的对角线AC，BD相交于点O，点E、F在AC上，且AE=CF．求证：BE=DF．
21. 如图，每个小正方形的边长都是1，△ABC的三个顶点分别在正方形网格的格点上．
(1)、求AB，BC的长；(2)、判断△ABC的形状，并说明理由．22. 我校举行“校园好声音”歌手大赛，初二级有两组各5名选手参加了年级初赛，需选出一组代表初二年级参加学校总决赛．两个组各选手的成绩（单位：分）如图所示．选手1
选手2
选手3
选手4
选手5
平均数
第一组
75
80
85
b
100
85
第二组
70
a
100
75
80
m
根据以上信息，解答下列问题：
(1)、a＝ ， b＝ ， m＝；(2)、请求出第一组初赛成绩的方差；(3)、经计算，第二组初赛成绩的方差S22＝160，你认为选择第几组代表初二年级参加学校总决赛更合适？请说明理由．23. 杆称是我国传统的计重工具，如图1，可以用秤砣到秤纽的水平距离x（厘米），来得出秤钩上所挂物体的重量y（斤）．如表中为若干次称重时所记录的一些数据．x（厘米）
1
2
4
7
11
y（斤）
0.75
1.00
1.50
2.25
3.25
(1)、请在图2平面直角坐标系中描出表中五组数据对应的点；(2)、秤钩上所挂物体的重量y是否为秤纽的水平距离的函数？如果是，请求出符合表中数据的函数解析式；(3)、当秤钩所挂物重是4.5斤时，秤杆上秤砣到秤纽的水平距离为多少厘米？24. 如图，在四边形ABCD中，AC、BD是对角线，点E、F、G、H分别是边AB、BC、CD、DA的中点，依次连接E、F、G、H．
(1)、证明：四边形EFGH是平行四边形；(2)、在四边形ABCD中，若再补充一个条件： ， 则四边形EFGH是矩形；(3)、连接EG、FH，求证：EG2＋FH2＝EF2＋FG2＋GH2＋HE225. 如图，在平面直角坐标系中，一次函数y＝﹣ x＋6的图象与坐标轴交于A、B点，AE平分∠BAO，交x轴于点E．
(1)、填空：点A的坐标是 ， 点B的坐标是；(2)、求直线AE的表达式；(3)、过点B作BF⊥AE，垂足为F，连接OF，试判断△OFB的形状，并求△OFB的面积．