安徽省宿州市泗县2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 下列图形中,既是中心对称图形又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 若a>b,则下列各式中,一定成立的是( )A、a+2<b+2 B、a-2<b-2 C、 > D、-2a>-2b3. 下列图形中,只用一种多边形不能镶嵌整个平面的是( )A、正三角形 B、正四边形 C、正六边形 D、正七边形4. 将分式 中的x,y的值同时扩大为原来的2021倍,则变化后分式的值( )A、扩大为原来的2021倍 B、缩小为原来的 C、保持不变 D、以上都不符合题意5. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )
2. 若a>b,则下列各式中,一定成立的是( )A、a+2<b+2 B、a-2<b-2 C、 > D、-2a>-2b3. 下列图形中,只用一种多边形不能镶嵌整个平面的是( )A、正三角形 B、正四边形 C、正六边形 D、正七边形4. 将分式 中的x,y的值同时扩大为原来的2021倍,则变化后分式的值( )A、扩大为原来的2021倍 B、缩小为原来的 C、保持不变 D、以上都不符合题意5. 如图,直线 的解析式为 ,直线 的解析式为 ,则不等式 的解集是( )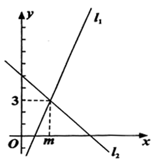 A、 B、 C、 D、6. 关于x的分式方程 有增根,则m的值是( )A、﹣2 B、3 C、﹣3 D、27. 用一条宽相等的足够长的纸条,打一个结,如下图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形 ABCDE,则∠BAC的度数是( )
A、 B、 C、 D、6. 关于x的分式方程 有增根,则m的值是( )A、﹣2 B、3 C、﹣3 D、27. 用一条宽相等的足够长的纸条,打一个结,如下图1所示,然后轻轻拉紧、压平就可以得到如图2所示的正五边形 ABCDE,则∠BAC的度数是( )
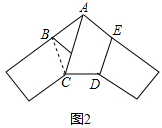 A、36° B、30° C、45° D、40°8. 平行四边形 的一边长为10,则它的两条对角线长可以是( )A、10和12 B、12和32 C、6和8 D、8和109. 用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设( )A、直角三角形中两个锐角都大于45° B、直角三角形中两个锐角都不大于45° C、直角三角形中有一个锐角大于45° D、直角三角形中有一个锐角不大于45°10. 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( )
A、36° B、30° C、45° D、40°8. 平行四边形 的一边长为10,则它的两条对角线长可以是( )A、10和12 B、12和32 C、6和8 D、8和109. 用反证法证明“直角三角形中至少有一个锐角不大于45°”,应先假设( )A、直角三角形中两个锐角都大于45° B、直角三角形中两个锐角都不大于45° C、直角三角形中有一个锐角大于45° D、直角三角形中有一个锐角不大于45°10. 如图,已知:∠MON=30°,点A1、A2、A3…在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,若OA1=1,则△A5B5A6的边长为( ) A、6 B、16 C、32 D、64
A、6 B、16 C、32 D、64二、填空题
-
11. 若代数式 有意义,则实数x的取值范围是.12. 正八边形的每个外角为度.
13. 分解因式14. 如图,已知 , 是 平分线上一点, ,交 于点 , ,垂足为点 ,且 ,则 等于.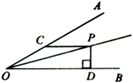 15. 如图,在□ 中, ,点 分别是 的中点,则 = .
15. 如图,在□ 中, ,点 分别是 的中点,则 = . 16. 不等式组 的解集是x>4,那么m的取值范围是 .17. 若关于 x 的分式方程 的解为正数,则 m 的取值范围是 .18. 如图,含45°角的直角三角板DBC的直角顶点D在∠BAC的角平分线AD上,DF⊥AB于F,DG⊥AC于G,将△DBC沿BC翻转,D的对应点落在E点处,当∠BAC=90°,AB=4,AC=3时,△ACE的面积等于 .
16. 不等式组 的解集是x>4,那么m的取值范围是 .17. 若关于 x 的分式方程 的解为正数,则 m 的取值范围是 .18. 如图,含45°角的直角三角板DBC的直角顶点D在∠BAC的角平分线AD上,DF⊥AB于F,DG⊥AC于G,将△DBC沿BC翻转,D的对应点落在E点处,当∠BAC=90°,AB=4,AC=3时,△ACE的面积等于 .
三、解答题
-
19. 先化简(x+1﹣ )÷ ,再从0,1,2中选出你喜欢的x的值代入求解.20. 在平面直角坐标系中的位置如图所示,其中每个小正方形的边长为1个单位长度.按要求作图:
 (1)、画出 关于原点 的中心对称图形 ;(2)、画出将 绕点 顺时针方向旋转90°得到的 .(3)、设 为 边上一点,在 上与点 对应的点是 .则点 坐标为 .21. 如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.
(1)、画出 关于原点 的中心对称图形 ;(2)、画出将 绕点 顺时针方向旋转90°得到的 .(3)、设 为 边上一点,在 上与点 对应的点是 .则点 坐标为 .21. 如图,已知四边形ABCD是平行四边形,点E,F是对角线BD上的两点,且BE=DF,连接AE,CF.求证:AE∥CF且AE=CF.
