安徽省安庆市2020-2021学年八年级下学期数学期末试卷
试卷更新日期:2021-09-02 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 下列关于 的一元二次方程中,有两个不相等的实数根的方程是( )A、 B、 C、 D、3. 下列根式中,与 不是同类二次根式的是( )A、 B、 C、 D、4. 某同学对数据 , , , , , 进行统计分析发现其中一个两位数的个位数字被墨水涂污看不到了,则计算结果与被涂污数字无关的是( )A、平均数 B、中位数 C、方差 D、众数5. 一个凸n边形,其每个内角都是140°,则n的值为( )A、6 B、7 C、8 D、96. 在 中, , , 的对边分别是 , , ,下列命题中的假命题是( ).A、若 ,则 不是直角三角形 B、若 ,则 是直角三角形 C、若 ,则 D、若 ,则 是直角三角形7. 已知实数 , 在数轴上的位置如图所示,化简: 的结果是( )
 A、 B、 C、 D、8. 据统计11月11日我省单日快递量比平时增加40%,到11月13日到达高峰,单日快递量为平时的3倍,设11日到13日单日快递量平均增长率为 ,则可列方程为( )A、 B、 C、 D、9. 观察分析下列数据,寻找规律:0, , ,3, , , ,…,那么第50个数据应该是( )A、 B、 C、 D、10. 如图, , , 、 两端在 的两边上滑动, 为等边三角形,则 的最小值为( )
A、 B、 C、 D、8. 据统计11月11日我省单日快递量比平时增加40%,到11月13日到达高峰,单日快递量为平时的3倍,设11日到13日单日快递量平均增长率为 ,则可列方程为( )A、 B、 C、 D、9. 观察分析下列数据,寻找规律:0, , ,3, , , ,…,那么第50个数据应该是( )A、 B、 C、 D、10. 如图, , , 、 两端在 的两边上滑动, 为等边三角形,则 的最小值为( ) A、 B、5 C、 D、2
A、 B、5 C、 D、2二、填空题
-
11. 二次根式 在实数范围内有意义,则 的取值范围是 .12. 设 , 是方程 的两个实数根,则 的值是 .13. 《九章算术》卷九“勾股”中记载:今有户不知高广,竿不知长短,横之不出四尺,纵之不出二尺,斜之适出,问户斜几何,意思是:一根竿子横放,竿比门宽长出四尺;竖放,竿比门高长出二尺,斜放恰好能出去,则竿长是尺.14. 如图,四边形纸片 中,点 , 分别在边 , 上,将纸片沿直线 折叠,点 恰好落在点 处;再将 , 分别沿 , 折叠,点 , 均落在 上的点 处.
 (1)、 的大小为°;(2)、若四边形 是菱形,点 为 中点且四边形纸片 的面积是 ,则 .
(1)、 的大小为°;(2)、若四边形 是菱形,点 为 中点且四边形纸片 的面积是 ,则 .三、解答题
-
15. 计算:16. 用配方法解方程 .17. 如图,已知四边形ABCD是平行四边形.
 (1)、作∠A的平分线交BC于点E.(用尺规作图,保留作图痕迹,不用写作法)(2)、在(1)中,若AD=6,EC=2,求平行四边形ABCD的周长.18. 已知关于x的一元二次方程x2﹣mx﹣2=0…①(1)、若x=﹣1是方程①的一个根,求m的值和方程①的另一根;(2)、对于任意实数m , 判断方程①的根的情况,并说明理由.19. 下面是 的网格
(1)、作∠A的平分线交BC于点E.(用尺规作图,保留作图痕迹,不用写作法)(2)、在(1)中,若AD=6,EC=2,求平行四边形ABCD的周长.18. 已知关于x的一元二次方程x2﹣mx﹣2=0…①(1)、若x=﹣1是方程①的一个根,求m的值和方程①的另一根;(2)、对于任意实数m , 判断方程①的根的情况,并说明理由.19. 下面是 的网格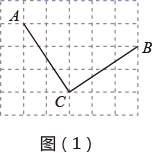
 (1)、如图(1), , , 是网格中的三个格点(即小正方形的顶点),判断 与 的数量和位置关系,直接写出结论,不需要说明理由;(2)、如图(2),求 的度数(要求:画出示意图并给出推导过程).20. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)、如图(1), , , 是网格中的三个格点(即小正方形的顶点),判断 与 的数量和位置关系,直接写出结论,不需要说明理由;(2)、如图(2),求 的度数(要求:画出示意图并给出推导过程).20. 如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.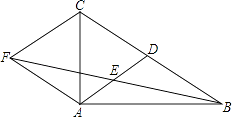 (1)、求证:AF=DC;(2)、若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.21. 某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下:
(1)、求证:AF=DC;(2)、若AB⊥AC,试判断四边形ADCF的形状,并证明你的结论.21. 某学校七年级、八年级各有500名学生,为了解两个年级的学生对垃圾分类知识的掌握情况,学校从七年级、八年级各随机抽取20名学生进行垃圾分类知识测试,满分100分,成绩整理分析过程如下:①(收集数据):七年级20名学生测试成绩统计如下:
67,58,64,56,69,70,95,84,74,77,78,78,71,86,91,86,86,92,86,70
②(整理数据):七年级20名学生测试成绩频数分布直方图(每组数据包括左端值不包括右端值,如最左边第一组的成绩范围为 ):

八年级20名学生测试成绩频数分布表:
成绩
人数
0
4
5
7
4
③分析数据,两组样本数据的平均数、中位数、众数、方差如下表所示:
年级
平均数
中位数
众数
方差
七年级
76.9
a
b
119.89
八年级
79.2
81
74
100.4
(1)、补全七年级20名学生测试成绩频数分布直方图;(2)、请直接写出 、 的值;(3)、请根据抽样调查数据,估计全校七年级垃圾分类知识测试成绩在80分及以上的大约有多少人;(4)、通过以上分析,你认为哪个年级学生对垃圾分类知识掌握得更好?请说明推断的理由(两条即可)22. 安庆某商场销售一批空气加湿器,平均每天可售出30台,每台可盈利50元,为了扩大销售量,增加盈利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每台每降价1元,商场平均每天可多售出2台.(1)、若该商场某天降价了5元,则当天可售出台,当天共盈利元.(2)、在尽快减少库存的前提下,商场每天要盈利2100元,每台空气加湿器应降价多少元?(3)、该商场平均每天盈利能达到2500元吗?如果能,求出此时应降价多少;如果不能,请说明理由.23. 已知,点 在正方形 的 边上(不与点 , 重合), 是对角线,延长 到点 ,使 ,过点 作 的垂线,垂足为 ,连接 , . (1)、根据题意补全图形,并证明 ;(2)、用等式表示线段 与 的数量关系,并证明.
(1)、根据题意补全图形,并证明 ;(2)、用等式表示线段 与 的数量关系,并证明.