初中数学湘教版九年级上册5.1总体平均数与方差的估计 同步练习

试卷更新日期：2021-09-02 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 在“开学考试”，“第1次月考”，“第2次月考”这三次考试中，小西，小南两名同学的数学平均分都是120分，小西数学成绩的方差是15，小南数学成绩的方差是3，则下列说法正确的是（   ）
    A、小西的成绩比小南稳定 B、小南的成绩比小西稳定 C、小西，小南成绩一样稳定 D、无法确定谁的成绩更稳定

    查看试题解析

  • 2. 某校开设了冰球选修课，12名同学被分成甲、乙两组进行训练，他们的身高（单位： cm ）如下图所示：

    设两队队员身高的平均数依次为 x¯甲 ， x¯乙 ，方差依次为 s甲2 ， s乙2 ，下列关系中完全正确的是（    ）

    A、x¯甲=x¯乙 ， s甲2<s乙2 B、x¯甲=x¯乙 ， s甲2>s乙2 C、x¯甲<x¯乙 ， s甲2<s乙2 D、x¯甲>x¯乙 ， s甲2>s乙2

    查看试题解析

  • 3. 老师要分析小刚的5次数学模拟考试成绩是否稳定，她需要统计小刚这5次成绩的（   ）
    A、平均数 B、方差或标准差 C、众数 D、中位数

    查看试题解析

  • 4. 为备战奥运会，甲、乙、丙、丁四位优秀短跑选手参加训练，近期的10次百米测试平均成绩都是10.3秒，但他们成绩的方差分别是0.020、0.019、0.021、0.022（单位：秒²）则这四人中发挥最稳定的是（   ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 5. 某车间对甲、乙、丙、丁四名生产工人一天生产出的各自20个零件长度进行调查。每位生产工人生产的零件长度的平均值均为10厘米，方差分别为S甲2=0.51，S乙2=1.5，S丙2=0.35，S丁2=0.75．其中生产出的零件长度最稳定的是（ ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 6. 某校七年级学生的平均年龄为13岁，年龄的方差为3，若学生人数没有变动，则两年后的同一批学生，对其年龄的说法正确的是（   ）
    A、平均年龄为13岁，方差改变 B、平均年龄为15岁，方差不变 C、平均年龄为15岁，方差改变 D、平均年龄为13岁，方差不变

    查看试题解析

  • 7. 某排球队6名场上队员的身高(单位：cm)是：180，184，188，190，192，194．现用一名身高为186cm的队员换下场上身高为192cm的队员，则与换人前相比，场上队员的身高的（ ）
    A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

    查看试题解析

  • 8. 甲、乙、丙三名射击运动员在某场测试中各射击20次，3人的测试成绩如下表．则甲、乙、丙3名运动员测试成绩最稳定的是（   ）

    甲的成绩

    乙的成绩

    丙的成绩

    环数

    7

    8

    9

    10

    环数

    7

    8

    9

    10

    环数

    7

    8

    9

    10

    频数

    4

    6

    6

    4

    频数

    6

    4

    4

    6

    频数

    5

    5

    5

    5
    A、甲 B、乙 C、丙 D、3人成绩稳定情况相同

    查看试题解析

  • 9. 某农场各用10块面积相同的试验田种植甲、乙两种大豆，收成后对两种大豆产量（单位：吨/亩）的数据统计如下： x¯甲≈0.54 ， x¯乙≈0.5 ， s甲2≈0.01 ， s乙2≈0.002 ，则由上述数据推断乙品种大豆产量比较稳定的依据是（   ）
    A、x¯甲>x¯乙 B、s甲2>s乙2 C、x¯甲>s甲2 D、x¯乙>s甲2

    查看试题解析

  • 10. 根据李飞与刘亮射击训练的成绩绘制了如图所示的折线统计图．

    根据图所提供的信息，若要推荐一位成绩较稳定的选手去参赛，应推荐（   ）

    A、李飞或刘亮 B、李飞 C、刘亮 D、无法确定

    查看试题解析

二、填空题

  • 11. 甲、乙两人参加“环保知识”竞赛，经过6轮比赛，他们的平均成绩都是97分.如果甲、乙两人比赛成绩的方差分别为 s甲 2=6.67, s乙2=2.50 ，则这6次比赛成绩比较稳定的是.（填“甲”或“乙”）

    查看试题解析

  • 12. 甲、乙两名运动员进行了5次百米赛跑测试，两人的平均成绩都是13.3秒，而S甲2=3.7，S乙2=6.25，则两人中成绩较稳定的是 ．

    查看试题解析

  • 13. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好是9.4环，方差分别是 S甲2=0 ． 90 ， S乙2=1.22 ， S丙2=0.43 ， S丁2=1.68 ，在本次射击测试中，成绩最稳定的是.

    查看试题解析

  • 14. 一组数据1，2，3，x，5的平均数是3，则该组数据的方差是 ．

    查看试题解析

  • 15. 据统计：2019年，邵阳市在教育扶贫方面，共资助学生91.3万人次，全市没有一名学生因贫失学，其中，某校老师承担了对甲，乙两名学生每周“送教上门”的任务，以下是甲、乙两名学生某十周每周接受“送教上门”的时间（单位：小时）：

    甲：7，8，8，9，7，8，8，9，7，9；

    乙：6，8，7，7，8，9，10，7，9，9．

    从接受“送教上门”的时间波动大小来看，学生每周接受送教的时间更稳定．（填“甲”或“乙”）

    查看试题解析

  • 16. 已知甲、乙两组数据的折线图如图，设甲、乙两组数据的方差分别为S甲2、S乙2 ， 则S甲2S乙2（填“＞”、“=”、“＜”）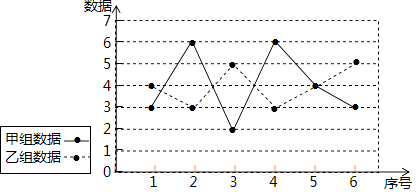

    查看试题解析

三、综合题

  • 17. 甲、乙两个电子厂在广告中都声称他们的某种电子产品在正常情况下的使用寿命都是5年.质检部门对这两家销售的产品的使用寿命进行了跟踪调查，统计结果如下：（单位：年）

    甲厂：3，4，5，6，7  乙厂：4，4，5，6，6

    (1)、分别求出甲、乙两厂的该种电子产品在正常情况下的使用寿命的平均数和方差；
    (2)、如果你是顾客，你会选购哪家电子厂的产品？说明理由.

    查看试题解析

  • 18. 甲、乙两人加工同一种直径为100mm的零件，现从他们加工好的零件中随机各抽取6个，量得零件的直径如下(单位：mm)：

    甲：98，102，100，100，101，99：

    乙：100，103，101，97，100，99．

    (1)、根据上述两组数据，完成下面的表格：

    平均数

    中位数

    众数

    方差

    甲

    100

    53

    乙

    100

    100

    (2)、请你结合(1)中的统计数据，评价一下甲、乙两人的加工质量．

    查看试题解析

  • 19. 某射击队教练为了了解队员训练情况，从队员中选取甲、乙两名队员进行射击测试，相同条件下各射靶5次，成绩统计如下：

    命中环数

    6

    7

    8

    9

    10

    甲命中相应环数的次数

    0

    1

    3

    1

    0

    乙命中相应环数的次数

    2

    0

    0

    2

    1

    (1)、根据上述信息可知：甲命中环数的中位数是环，乙命中环数的众数是环；
    (2)、试通过计算说明甲、乙两人的成绩谁比较稳定？
    (3)、如果乙再射击1次，命中8环，那么乙射击成绩的方差会 ． （填 “变大”、“变小” 或 “不变”）

    查看试题解析

  • 20. 甲、乙两台机床同时加工直径为 10mm 的同种规格零件，为了检查两台机床加工零件的稳定性，质检员从两台机床的产品中各抽取 5 件进行检测，结果如下（单位： mm ）：

    甲

    10

    9.8

    10

    10.2

    10

    乙

    9.9

    10

    10

    10.1

    10

    (1)、分别求出这两台机床所加工零件直径的平均数和方差；
    (2)、根据所学的统计知识，你认为哪一台机床生产零件的稳定性更好一些，说明理由.

    查看试题解析

  • 21. 某商场统计了A、B两种品牌洗衣机7个月的销售情况，结果如下：

    一月

    二月

    三月

    四月

    五月

    六月

    七月

    A品牌

    16

    31

    29

    24

    24

    24

    20

    B品牌

    16

    20

    24

    25

    26

    27

    30
    (1)、分别求这7个月A、B两种品牌洗衣机销量的方差；
    (2)、由于库存不足，商场采购部欲从厂家采购A、B两种品牌洗衣机以满足市场需求.请你结合上述两种品牌洗衣机的销售情况，对商场采购部提出建议，并从两个不同角度说明理由.

    查看试题解析