北师版数学九年级上册《第三章 概率的进一步认识》单元检测A卷
试卷更新日期:2021-09-01 类型:单元试卷
一、单选题
-
1. 妙妙上学经过两个路口,如果每个路口可直接通过和需等待的可能性相等,那么妙妙上学时在这两个路口都直接通过的概率是( )A、 B、 C、 D、2. 学校招募运动会广播员,从两名男生和两名女生共四名候选人中随机选取两人,则两人恰好是一男一女的概率是( )A、 B、 C、 D、3. 同时掷两枚质地均匀的骰子,则两枚骰子向上的点数之和为7的概率是( )A、 B、 C、 D、4. 现有4张卡片,正面图案如图所示,它们除此之外完全相同.把这4张卡片背面朝上洗匀,从中随机抽取两张,则这两张卡片正面图案恰好是“天问”和“九章”的概率是( )
 A、 B、 C、 D、5. 小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )A、 B、 C、 D、6. 工厂从三名男工人和两名女工人中,选出两人参加技能大赛,则这两名工人恰好都是男工人的概率为( )A、 B、 C、 D、7. 有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )A、 B、 C、 D、8. 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )A、 B、 C、 D、9. 经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为( )A、 B、 C、 D、10. 柜子里有两双不同的鞋,如果从中随机地取出2只,那么取出的鞋是同一双的概率为( )A、 B、 C、 D、11. 有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为( )A、 B、 C、 D、12. 如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )
A、 B、 C、 D、5. 小颖有两顶帽子,分别为红色和黑色,有三条围巾,分别为红色、黑色和白色,她随机拿出一顶帽子和一条围巾戴上,恰好为红色帽子和红色围巾的概率是( )A、 B、 C、 D、6. 工厂从三名男工人和两名女工人中,选出两人参加技能大赛,则这两名工人恰好都是男工人的概率为( )A、 B、 C、 D、7. 有一枚质地均匀的正方体骰子,六个面上分别刻有1到6的点数.将它投掷两次,则两次掷得骰子朝上一面的点数之和为5的概率是( )A、 B、 C、 D、8. 某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等。某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )A、 B、 C、 D、9. 经过某路口的汽车,可能直行,也可能左拐或右拐.假设这三种可能性相同,现有两车经过该路口,恰好有一车直行,另一车左拐的概率为( )A、 B、 C、 D、10. 柜子里有两双不同的鞋,如果从中随机地取出2只,那么取出的鞋是同一双的概率为( )A、 B、 C、 D、11. 有一首《对子歌》中唱到:天对地,雨对风,大陆对长空.现将“天,雨,大,空”四个字书写在材质、大小完全相同的卡片上,在暗箱搅匀后,随机抽取两张,恰为“天”、“空”二字的概率为( )A、 B、 C、 D、12. 如图所示的两个转盘分别被均匀地分成5个和4个扇形,每个扇形上都标有数字,同时自由转动两个转盘,转盘停止后,指针都落在奇数上的概率是( )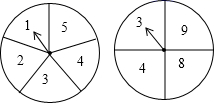 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 社团课上,同学们进行了“摸球游戏”:在一个不透明的盒子里装有几十个除颜色不同外其余均相同的黑、白两种球,将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程.整理数据后,制作了“摸出黑球的频率”与“摸球的总次数”的关系图象如图所示,经分析可以推断盒子里个数比较多的是(填“黑球”或“白球”).
 14. 贵阳市2021年中考物理实验操作技能测试中,要求学生两人一组合作进行,并随机抽签决定分组.有甲、乙、丙、丁四位同学参加测试,则甲、乙两位同学分到同一组的概率是.15. 从-1, ,2中任取两个不同的数作积,则所得积的中位数是.16. 不透明的布袋中有红、黄、蓝3种只是颜色不同的钢笔各1支,先从中摸出1支,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1支,记录下颜色,那么这两次摸出的钢笔为红色、黄色各一支的概率为.17. 我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和如图1, 是该三角形的顺序旋转和, 是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数k,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是.
14. 贵阳市2021年中考物理实验操作技能测试中,要求学生两人一组合作进行,并随机抽签决定分组.有甲、乙、丙、丁四位同学参加测试,则甲、乙两位同学分到同一组的概率是.15. 从-1, ,2中任取两个不同的数作积,则所得积的中位数是.16. 不透明的布袋中有红、黄、蓝3种只是颜色不同的钢笔各1支,先从中摸出1支,记录下它的颜色,将它放回布袋并搅匀,再从中随机摸出1支,记录下颜色,那么这两次摸出的钢笔为红色、黄色各一支的概率为.17. 我们对一个三角形的顶点和边都赋给一个特征值,并定义:从任意顶点出发,沿顺时针或逆时针方向依次将顶点和边的特征值相乘,再把三个乘积相加,所得之和称为此三角形的顺序旋转和或逆序旋转和如图1, 是该三角形的顺序旋转和, 是该三角形的逆序旋转和.已知某三角形的特征值如图2,若从1,2,3中任取一个数作为x,从1,2,3,4中任取一个数作为y,则对任意正整数k,此三角形的顺序旋转和与逆序旋转和的差都小于4的概率是.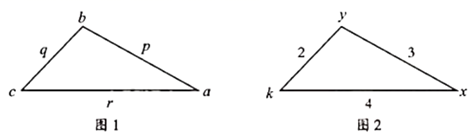 18. 如图所示,电路连接完好,且各元件工作正常随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是 .
18. 如图所示,电路连接完好,且各元件工作正常随机闭合开关 , , 中的两个,能让两个小灯泡同时发光的概率是 .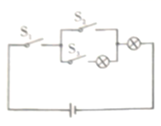
三、解答题
-
19. 如图,是一个竖直放置的钉板,其中,黑色圆面表示钉板上的钉子, 分别表示相邻两颗钉子之间的空隙,这些空隙大小均相等,从入口 处投放一个直径略小于两颗钉子之间空隙的圆球,圆球下落过程中,总是碰到空隙正下方的钉子,且沿该钉子左右两个相邻空隙继续下落的机会相等,直至圆球落入下面的某个槽内.用画树状图的方法,求圆球落入③号槽内的概率.
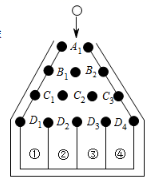 20. 第一盒中有1个白球、1个黑球,第二盒中有1个白球,2个黑球.这些球除颜色外无其他差别,分别从每个盒中随机取出1个球,用画树状图或列表的方法,求取出的2个球都是白球的概率.21. 如图,甲、乙两个转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙两个转盘中指针所指数字分别记为x , y . 请用树状图或列表法求点 落在平面直角坐标系第一象限内的概率.
20. 第一盒中有1个白球、1个黑球,第二盒中有1个白球,2个黑球.这些球除颜色外无其他差别,分别从每个盒中随机取出1个球,用画树状图或列表的方法,求取出的2个球都是白球的概率.21. 如图,甲、乙两个转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙两个转盘中指针所指数字分别记为x , y . 请用树状图或列表法求点 落在平面直角坐标系第一象限内的概率. 22. 小华有三张卡片,小明有两张卡片,卡片除正面上的数字不同外其它都相同,卡片上的数字如图所示.小华从自己的三张卡片中随机抽取一张,之后小明也从自己的两张卡片中随机抽取一张,请用画树状图(或列表)的方法,求抽取的两张卡片上的数字和为7的概率.
22. 小华有三张卡片,小明有两张卡片,卡片除正面上的数字不同外其它都相同,卡片上的数字如图所示.小华从自己的三张卡片中随机抽取一张,之后小明也从自己的两张卡片中随机抽取一张,请用画树状图(或列表)的方法,求抽取的两张卡片上的数字和为7的概率. 23. 某中学举行“中国梦•我的梦”演讲比赛.九年级(1)班的小明和小刚都想参加.现设计了如下游戏规则:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去,这个游戏规则是否公平?并说明理由.24. “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马 ,田忌也有上、中、下三匹马 ,且这六匹马在比赛中的胜负可用不等式表示如下: (注: 表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵( )获得了整场比赛的胜利,创造了以弱胜强的经典案例.
23. 某中学举行“中国梦•我的梦”演讲比赛.九年级(1)班的小明和小刚都想参加.现设计了如下游戏规则:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去,这个游戏规则是否公平?并说明理由.24. “田忌赛马”的故事闪烁着我国古代先贤的智慧光芒.该故事的大意是:齐王有上、中、下三匹马 ,田忌也有上、中、下三匹马 ,且这六匹马在比赛中的胜负可用不等式表示如下: (注: 表示A马与B马比赛,A马获胜).一天,齐王找田忌赛马,约定:每匹马都出场比赛一局,共赛三局,胜两局者获得整场比赛的胜利.面对劣势,田忌事先了解到齐王三局比赛的“出马”顺序为上马、中马、下马,并采用孙膑的策略:分别用下马、上马、中马与齐王的上马、中马、下马比赛,即借助对阵( )获得了整场比赛的胜利,创造了以弱胜强的经典案例.假设齐王事先不打探田忌的“出马”情况,试回答以下问题:
(1)、如果田忌事先只打探到齐王首局将出“上马”,他首局应出哪种马才可能获得整场比赛的胜利?并求其获胜的概率;(2)、如果田忌事先无法打探到齐王各局的“出马”情况,他是否必败无疑?若是,请说明理由;若不是,请列出田忌获得整场比赛胜利的所有对阵情况,并求其获胜的概率.25. 学完统计知识后,小明对同学们最近一周的睡眠情况进行随机抽样调查,得到他们每日平均睡眠时长 (单位:小时)的一组数据,将所得数据分为四组(A: ;B: ;C: ;D: ),并绘制成如下两幅不完整的统计图.
根据以上信息,解答下列问题:
(1)、小明一共抽样调查了名同学;在扇形统计图中,表示D组的扇形圆心角的度数为;(2)、将条形统计图补充完整;(3)、小明所在学校共有I400名学生,估计该校最近一周大约有多少名学生睡眠时长不足8小时?(4)、A组的四名学生是2名男生和2名女生,若从他们中任选2人了解最近一周睡眠时长不足8小时的原因,试求恰好选中1名男生和I名女生的概率.