北师版数学九年级上册同步训练《3.1 用树状图或表格求概率》

试卷更新日期：2021-09-01 类型：同步测试

进入出卷网下载

一、单选题

1. 同时抛掷两枚质地均匀的硬币，则一枚硬币正面向上､一枚硬币反面向上的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
2. 疫情期间进入学校都要进入测温通道，体温正常才可进入学校，昌平某校有2个测温通道，分别记为A、B通道，学生可随机选取其中的一个通道测温进校园．某日早晨该校所有学生体温正常．小王和小李两同学该日早晨进校园时，选择同一通道测温进校园的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{2}{3}$

查看试题解析
3. 学校组织学生外出集体劳动时，为九年级学生安排了三辆车．九年级的小明与小亮都可以从这三辆车中任选一辆搭乘，则他俩搭乘同一辆车的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{2}{3}$ C、 $\frac{1}{7}$ D、 $\frac{3}{4}$

查看试题解析
4. 小明计划到永州市体验民俗文化，想从“零陵渔鼓、瑶族长鼓舞、东安武术、舜帝祭典”四种民俗文化中任意选择两项，则小明选择体验“瑶族长鼓舞、舜帝祭典”的概率为（）

A、 $\frac{1}{3}$ B、 $\frac{1}{4}$ C、 $\frac{3}{4}$ D、 $\frac{1}{6}$

查看试题解析
5. 如图，一条毛毛虫要从A处去吃树叶，毛毛虫在交叉路口处选择任何树枝都是等可能的，它吃到树叶的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析
6. 男生昊昊、明明与女生贝贝、晶晶同在“黄梅飘香”社团，现要在该四人中随机挑选2名同学上台表演，那么恰好挑选到昊昊和一名女同学的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{2}{3}$

查看试题解析
7. 学校要举行运动会，小亮和小刚报名参加100米短跑项目的比赛，预赛分A ， B ， C三组进行，小亮和小刚恰好在同一个组的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{3}$ C、 $\frac{1}{6}$ D、 $\frac{1}{9}$

查看试题解析
8. $A$ 、 $B$ 、 $C$ 、 $D$ 四个人玩扑克牌游戏，他们先取出两张红桃和两张黑桃共四张扑克牌，洗匀后背面朝上放在桌面上，每人抽取其中一张，拿到相同颜色扑克牌的两个人为游戏搭档，若 $A$ 、 $B$ 两人各抽取了一张扑克牌，则两人恰好成为游戏搭档的概率为（）

A、 $\frac{1}{6}$ B、 $\frac{1}{3}$ C、 $\frac{1}{2}$ D、 $\frac{3}{4}$

查看试题解析
9. 如图，电路图上有4个开关和1个小灯泡，同时闭合2个开关，小灯泡发光的概率是（）

A、 $\frac{1}{4}$ B、 $\frac{3}{4}$ C、 $\frac{1}{2}$ D、 $\frac{1}{3}$

查看试题解析
10. 甲袋中装有2张相同的卡片，颜色分别为红色和黄色；乙袋中装有3张相同的卡片，颜色分别为红色、黄色、绿色．从这两个口袋中各随机抽取1张卡片，取出的两张卡片中至少有一张是红色的概率是（　　）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{1}{3}$ D、 $\frac{1}{6}$

查看试题解析

二、填空题

11. 端午节是我国传统佳节，小峰同学带了4个粽子(除粽馅不同外，其他均相同)，其中有两个肉馅粽子、一个红枣粽子和一个豆沙粽子，准备从中任意拿出两个送给他的好朋友小悦，小悦拿到的两个粽子都是肉馅的概率是

查看试题解析
12. 盒子里有4张形状、大小、质地完全相同的卡片，上面分别标着数字2，3，4，5，从中随机抽出1张后不放回，再随机抽出1张，则两次抽出的卡片上的数字之和为偶数的概率是.

查看试题解析
13. 一个不透明的口袋中有两个完全相同的小球，把它们分别标号为1，2．随机摸取一个小球后，放回并摇匀，再随机摸取一个小球，两次取出的小球标号的和等于4的概率为．

查看试题解析

14. 看了《田忌赛马》故事后，小杨用数学模型来分析齐王与田忌的上中下三个等级的三匹马记分如表，每匹马只赛一场，两数相比，大数为胜，三场两胜则赢．已知齐王的三匹马出场顺序为10，8，6．若田忌的三匹马随机出场，则田忌能赢得比赛的概率为．

马匹

姓名

下等马

中等马

上等马

齐王

田忌

查看试题解析

15. 不透明袋子中装有黑球1个、白球2个，这些球除了颜色外无其他差别.从袋子中随机摸出一个球，记下颜色后放回，将袋子中的球摇匀，再随机摸出一个球，记下颜色，前后两次摸出的球都是白球的概率是.

查看试题解析
16. 几何图形嵌板是一种开发幼儿智力的玩具．如图，甲，乙两个小朋友分别从 $A$ ， $B$ ， $C$ ， $D$ 四个嵌板中随机抓取一个，放在操作屉中，则他们抓取相同嵌板的概率为．

查看试题解析

三、解答题

17. “航天知识竞赛”活动中，获得“小宇航员”称号的小明得到了A、B、C三枚纪念章．如图，A、B、C三枚纪念章正面上分别印有“嫦娥五号”、“天问一号”和“天宫一号”的图案．三枚纪念章除正面图案不同外，其余均相同，小明将这三枚纪念章背面朝上放在桌面上，然后从中随机选取一枚，记下图案并放回，重新洗匀后再从中随机抽取一张．请用画树状图（或列表）的方法，求小明两次抽到图案上至少有一张印有“嫦娥五号”图案的概率．

查看试题解析
18. 在四编号为A，B，C，D的卡片（除编号外，其余完全相同）的正面分别写上如图所示正整数后，背面朝上，洗匀放好，现从中随机抽取一张（不放回），再从剩下的卡片中机抽取一张．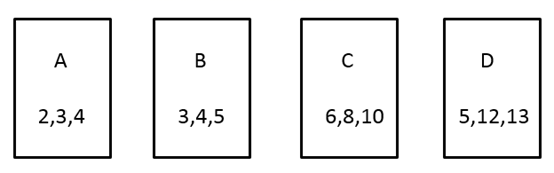
我们知道，满足 $a^{2} + b^{2} = c^{2}$ 的三个正整数a，b，c成为勾股数，请用“列表法”或“树状图法”求抽到的两张卡片上的数都是勾股数的概率（卡片用A，B，C，D表示）．

查看试题解析
19. 甲、乙两名同学玩一个游戏：在一个不透明的口袋中装有三个小球，分别标有数字1、2、3，这些小球除数字不同外其余均相同．甲先从口袋中随机摸出一个小球记下数字后放回，搅匀后乙再从口袋中随机摸出一个小球．若两次摸出的小球上数字之和是偶数则甲获胜；若两次摸出的小球上数字之和是奇数，则乙获胜．用画树状图或列表的方法，说明这个游戏对双方是否公平．

查看试题解析
20. 从－3，－1，1，3中任取一个值作为横坐标 $a$ ，不放回再任取一个作为纵坐标 $b$ ，请用树状图或列表的方法求点 $M (a ， b)$ 在双曲线 $y = \frac{3}{x}$ 的图象上的概率．

查看试题解析
21. 经过设有交通指示灯的路口时可能遇到红灯，也可能遇到黄灯或绿灯，假设这三种可能性相同.现小亮要连续通过前方的两个设有交通指示灯且运转正常的路口，请用列表法或画树状图法，求小亮至少遇到一次绿灯的概率.

查看试题解析
22. 如图，有两个可以自由转动的转盘A、B，转盘A被均匀分成4等份，每份标上数字1、2、3、4四个数字；转盘B被均匀分成6等份，每份标上数字1、2、3、4、5、6六个数字．有人为甲乙两人设计了一个游戏，其规则如下：
同时转动转盘A与B，转盘停止后，指针各指向一个数字（如果指针恰好指在分割线上，那么重转一次，直到指针指向一个数字为止），用所指的两个数字作乘积，如果所得的积是偶数，那么甲得1分；如果所得的积是奇数，那么乙得1分．你认为这样的规则是否公平？请你说明理由；如果不公平，请你修改规则使该游戏对双方公平．

查看试题解析