高中数学人教A版（2019）选择性必修一第一章空间向量的应用表示同步练习

试卷更新日期：2021-09-01 类型：同步测试

进入出卷网下载

一、单选题

1. 在正方体ABCD－A₁B₁C₁D₁中，E是C₁D₁的中点，则异面直线DE与AC所成角的余弦值为（）

A、 $\frac{1}{20}$ B、 $\frac{\sqrt{10}}{10}$ C、 $- \frac{\sqrt{10}}{10}$ D、 $- \frac{1}{20}$

查看试题解析
2. 三棱锥 $S - A B C$ 中， $S A ⊥$ 底面ABC， $S A = 4$ ， $A B = 3$ ，D为AB的中点， $∠ A B C = 90 °$ ，则点D到面 $S B C$ 的距离等于（）

A、 $\frac{12}{5}$ B、 $\frac{9}{5}$ C、 $\frac{6}{5}$ D、 $\frac{3}{5}$

查看试题解析
3. 蹴鞠是古人用脚、蹋、踢皮球的活动，类似今日的足球运动，2006年5月20日经国务院批准列入第一批国家非物质文化遗产名录，蹴鞠所用之鞠（球）一般比现代足球直径略小，已知一足球直径为22cm，其球心到截面圆 $O_{1}$ 的距离为9cm，若某跋鞠（球）的最大截面圆的面积恰好等于圆 $O_{1}$ 的面积，则该蹴鞠（球）的直径所在的区间是（）（单位：cm）

A、 $[10 ， 11)$ B、 $[11 ， 12)$ C、 $[12 ， 13)$ D、 $[13 ， 14]$

查看试题解析
4. 在棱长为1的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ 为 $C C_{1}$ 的中点，则直线 $A_{1} B$ 与平面 $B D E$ 所成角为（）

A、 $\frac{π}{6}$ B、 $\frac{π}{3}$ C、 $\frac{π}{2}$ D、 $\frac{5}{6} π$

查看试题解析
5. 如图，点 $P$ 为矩形 $A B C D$ 所在平面外一点， $P A ⊥$ 平面 $A B C D$ ， $Q$ 为 $A P$ 的中点， $A B = 3$ ， $B C = 4$ ， $P A = 2$ ，则点 $P$ 到平面 $B Q D$ 的距离为（）

A、 $\frac{5}{13}$ B、 $\frac{12}{13}$ C、 $\frac{13}{5}$ D、 $\frac{13}{12}$

查看试题解析
6. 四棱锥 $S - A B C D$ 中，侧面 $S B C$ 为等边三角形，底面 $A B C D$ 为矩形， $B C = 2$ ， $A B = a$ ，点 $F$ 是棱 $A D$ 的中点，顶点 $S$ 在底面 $A B C D$ 的射影为 $H$ ，则下列结论正确的是（）

A、棱 $S C$ 上存在点 $P$ 使得 $P D //$ 面 $B S F$ B、当 $H$ 落在 $A D$ 上时， $a$ 的取值范围是 $(0 ， \sqrt{3}]$ C、当 $H$ 落在 $A D$ 上时，四棱锥 $S - A B C D$ 的体积最大值是2 D、存在 $a$ 的值使得点 $B$ 到面 $S F C$ 的距离为 $\sqrt{3}$

查看试题解析
7. 如图，正三角形 $A C B$ 与正三角形 $A C D$ 所在平面互相垂直，则二面角 $B - C D - A$ 的余弦值是（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{2}}{2}$ C、 $\frac{\sqrt{3}}{3}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
8. 如图，在正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $M$ 为线段 $A_{1} D$ 的中点， $N$ 为线段 $C D_{1}$ 上的动点，则直线 $C_{1} D$ 与直线 $M N$ 所成角正弦值的最小值为（）

A、 $\frac{\sqrt{3}}{2}$ B、 $\frac{\sqrt{6}}{6}$ C、 $\frac{\sqrt{6}}{3}$ D、 $\frac{\sqrt{6}}{4}$

查看试题解析

二、多选题

9. 如图是长方体的平面展开图， $A B = 3$ ， $B E = 2$ ， $B C = 4$ ，则在该长方体中（）

A、 $B$ ， $C$ ， $F$ ， $G$ 四点共面 B、直线 $A E$ 与直线 $G C$ 平行 C、直线 $B H$ 与平面 $A C G$ 的距离为3 D、三棱锥 $B - D F H$ 外接球的表面积为 $29 π$

查看试题解析
10. 正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ ，的棱长为4，已知 $A C_{1} ⊥$ 平面α ， $A C_{1} \subset β$ ，则关于α､β截此正方体所得截面的判断正确的是（）

A、α截得的截面形状可能为正三角形 B、 $A A_{1}$ 与截面α所成角的余弦值为 $\frac{\sqrt{6}}{3}$ C、α截得的截面形状可能为正六边形 D、β截得的截面形状可能为正方形

查看试题解析
11. 如图，平面 $α \cap$ 平面 $β =$ 直线 $l$ ，点 $A ， C \in α$ ，点 $B ， D \in β$ ，且 $A 、 B 、 C 、 D \notin l$ ，点 $M$ 、 $N$ 分别是线段 $A B$ 、 $C D$ 的中点.（）

A、当直线 $A C$ 与 $B D$ 相交时，交点一定在直线 $l$ 上 B、当直线 $A B$ 与 $C D$ 异面时， $M N$ 可能与 $l$ 平行 C、当 $A$ 、 $B$ 、 $C$ 、 $D$ 四点共面且 $A C // l$ 时， $B D // l$ D、当 $M$ 、 $N$ 两点重合时，直线 $A C$ 与 $l$ 不可能相交

查看试题解析
12. 如图，在菱形 $A B C D$ 中， $A B = 2$ ， $∠ B A D = 60 °$ ，将 $△ A B D$ 沿对角线 $B D$ 翻折到 $△ C B D$ 位置，则在翻折的过程中，下列说法正确的（）

A、存在某个位置，使得 $P C = 3$ B、存在某个位置，使得 $P B ⊥ C D$ C、存在某个位置，使得 $P$ ， $B$ ， $C$ ， $D$ 四点落在半径为 $\frac{\sqrt{6}}{2}$ 的球面上 D、存在某个位置，使得点 $B$ 到平面 $P D C$ 的距离为 $\sqrt{3}$

查看试题解析

三、填空题

13. 已知球 $O$ 是三棱锥 $P - A B C$ 的外接球， $P A = A B = P B = A C = 2$ ， $C P = 2 \sqrt{2}$ ，点 $D$ 是 $P B$ 的中点，且 $C D = \sqrt{7}$ ，则球 $O$ 的表面积为.

查看试题解析
14. 在四棱锥 $S - A B C D$ 中，四边形 $A B C D$ 为正方形， $A B = 2$ ， $D S = 1$ ，平面 $A S D ⊥$ 平面 $A B C D$ ， $S D ⊥ A D$ ，点 $E$ 为 $D C$ 上的动点，平面 $B S E$ 与平面 $A S D$ 所成的二面角为 $θ$ （ $θ$ 为锐角），则当 $θ$ 取最小值时，三棱锥 $E - A S D$ 的体积为.

查看试题解析
15. 如图，在棱长为4的正方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中，M是棱 $A_{1} A$ 上的动点，N是棱 $B C$ 的中点.当平面 $D_{1} M N$ 与底面 $A B C D$ 所成的锐二面角最小时， $A_{1} M =$ .

查看试题解析
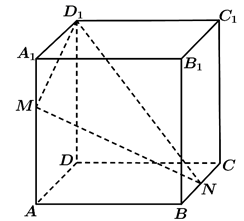16. 三棱锥P-ABC中，PA ， PB ， PC两两垂直， $P A = P B = P C = \sqrt{6}$ ，点Q为平面ABC内的动点，且满足 $P Q = \sqrt{3}$ ，记直线PQ与直线AB的所成角为 $θ$ ，则 $\sin θ$ 的取值范围为.

查看试题解析

四、解答题

17. 在四棱锥 $P - A B C D$ 中， $P D ⊥$ 底面ABCD， $A B // D C$ ， $∠ A D C = 120 °$ ，BD平分 $∠ A D C$ ， $D C = P D = 2 A B = 2 A D$ .

(1)、证明： $B C ⊥ P B$ ；

(2)、求二面角 $A - P B - C$ 的余弦值.

查看试题解析
18. 如图，在四棱锥 $P - A B C D$ 中，四边形 $A B C D$ 为矩形， $P A ⊥$ 平面 $A B C D$ ， $M$ 是 $P C$ 的中点， $P A = A D = 2$ ， $A B = 1$ .

(1)、求证： $P A //$ 平面 $M B D$

(2)、求点 $D$ 到平面 $P B C$ 的距离.

查看试题解析
19. 如图，在长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 中， $E$ ， $F$ 分别为 $A B$ ， $B C$ 的中点，点 $P$ 为面 $A_{1} B_{1} C_{1} D_{1}$ 内的一点．

(1)、画出图1中平面 $P E F$ 与平面 $B_{1} B C C_{1}$ 的交线；

(2)、如图2，若 $P$ 为矩形 $A_{1} B_{1} C_{1} D_{1}$ 对角线的交点， $A B = 6$ ， $B C = 4$ ， $B B_{1} = 2$ ，求点 $B$ 到平面 $P E F$ 的距离．

查看试题解析
20. 已知四棱锥 $S - A B C D$ 中，四边形 $A B C D$ 是菱形，且 $∠ A B C = 120 °$ ， $Δ S B C$ 为等边三角形，平面 $S B C ⊥$ 平面 $A B C D$ ．

(1)、求证： $B C ⊥ S D$ ；

(2)、若点 $E$ 是线段 $S A$ 上靠近 $S$ 的三等分点，求直线 $D E$ 与平面 $S A B$ 所成角的正弦值．

查看试题解析
21. 如图，长方体 $A B C D - A_{1} B_{1} C_{1} D_{1}$ 的底面 $A B C D$ 是正方形，点 $E$ 在棱 $A A_{1}$ 上， $B E ⊥ E C_{1}$ ．

(1)、证明： $B E ⊥$ 平面 $E B_{1} C_{1}$ ；

(2)、若 $A E = A_{1} E$ ， $A D = 1$ ，求二面角 $B - E C - C_{1}$ 的余弦值．

查看试题解析
22. 已知在六面体 $P A B C D E$ 中， $P A ⊥$ 平面 $A B C D$ ， $E D ⊥$ 平面 $A B C D$ ，且 $P A = 2 E D$ ，底面 $A B C D$ 为菱形，且 $∠ A B C = 60 °$ .

(1)、求证：平面 $P A C ⊥$ 平面 $P B D$ ；

(2)、若直线 $P C$ 与平面 $A B C D$ 所成角为 $45 °$ ，试问：在线段 $P E$ 上是否存在点 $M$ ，使二面角 $P - A C - M$ 为 $60 °$ ？若存在，确定点 $M$ 的位置；若不存在，请说明理由.

查看试题解析