山西省晋中市寿阳县2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1. 计算a2•a3的结果是( )A、5a B、a5 C、a6 D、a82. 冬季奥林匹克运动会是世界规模最大的冬季综合性运动会,每四年举办一次,第24届冬奥会将于2022年在北京和张家口举办.下列四个图分别是第24届冬奥会图标中的一部分,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 若气象部门预报明天下雨的概率是70%,下列说法正确的是( )A、明天下雨的可能性比较大 B、明天一定不会下雨 C、明天一定会下雨 D、明天下雨的可能性比较小4. 下列四个图形中, 和 是内错角的是( )A、
3. 若气象部门预报明天下雨的概率是70%,下列说法正确的是( )A、明天下雨的可能性比较大 B、明天一定不会下雨 C、明天一定会下雨 D、明天下雨的可能性比较小4. 下列四个图形中, 和 是内错角的是( )A、 B、
B、 C、
C、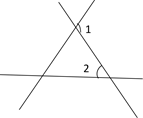 D、
D、 5. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )
5. 如图,一扇窗户打开后,用窗钩AB可将其固定,这里所运用的几何原理是( )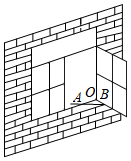 A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短6. 如图,测量河两岸相对的两点A,B的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△ABC的依据是( )
A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短6. 如图,测量河两岸相对的两点A,B的距离时,先在AB的垂线BF上取两点C,D,使CD=BC,再过点D画出BF的垂线DE,当点A,C,E在同一直线上时,可证明△EDC≌△ABC,从而得到ED=AB,则测得ED的长就是两点A,B的距离.判定△EDC≌△ABC的依据是( ) A、“边边边” B、“角边角” C、“全等三角形定义” D、“边角边”7. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、
A、“边边边” B、“角边角” C、“全等三角形定义” D、“边角边”7. 用三角板作△ABC的边BC上的高,下列三角板的摆放位置正确的是( )A、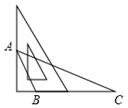 B、
B、 C、
C、 D、
D、 8. 如图,△ABC 中,∠B=60°,∠C=50°,点 D 是 BC 上任一点,点 E 和点 F 分别是点 D 关于 AB 和 AC 的对称点,连接 AE 和 AF,则∠EAF 的度数是( )
8. 如图,△ABC 中,∠B=60°,∠C=50°,点 D 是 BC 上任一点,点 E 和点 F 分别是点 D 关于 AB 和 AC 的对称点,连接 AE 和 AF,则∠EAF 的度数是( ) A、140° B、135° C、120° D、100°9. 适合条件∠A= ∠B= ∠C的△ABC是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形10. 如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等.
A、140° B、135° C、120° D、100°9. 适合条件∠A= ∠B= ∠C的△ABC是( )A、锐角三角形 B、直角三角形 C、钝角三角形 D、等边三角形10. 如图,AB=12m,CA⊥AB于点A,DB⊥AB于点B,且AC=4m,点P从B向A运动,每分钟走1m,点Q从B向D运动,每分钟走2m,P、Q两点同时出发,运动( )分钟后,△CAP与△PQB全等. A、2 B、3 C、4 D、8
A、2 B、3 C、4 D、8二、填空题
-
11. 芝麻被称为“八谷之冠”,是世界上最古老的油料作物之一,它作为食品和药物,得到广泛的使用。经测算,一粒芝麻的质量约为0.00000201千克,将0.00000201用科学记数法表示为 .12. 如图,一飞镖游戏板由大小相等的小正方形格子构成,向游戏板随机投掷一枚飞镖,击中黑色区域的概率是.
 13. 端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离S(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是点.
13. 端午节三天假期的某一天,小明一家上午8点自驾小汽车从家出发,到某旅游景点游玩,该小汽车离家的距离S(千米)与离家的时间t(时)的关系如图所示,则小明一家开车回到家的时间是点. 14. 如图,点P在∠AOB的平分线上,∠AOB=60°,PD⊥OA于D,点M在OP上,且DM=MP=6,若C是OB上的动点,则PC的最小值是 .
14. 如图,点P在∠AOB的平分线上,∠AOB=60°,PD⊥OA于D,点M在OP上,且DM=MP=6,若C是OB上的动点,则PC的最小值是 . 15. 已知:如图,在△ABC,BD⊥AC,CF⊥AB垂足分别为点D、F,线段BD、CF交于点E,若∠A=70°,则∠BEC= .
15. 已知:如图,在△ABC,BD⊥AC,CF⊥AB垂足分别为点D、F,线段BD、CF交于点E,若∠A=70°,则∠BEC= .
三、解答题
-
16. 计算:(1)、 .(2)、(2x2y)3•(﹣7xy2)÷14x4y3 .(3)、(x+4)2﹣(x﹣2)(x+5).(4)、(x+y﹣z)(x﹣y+z).17. 先化简再求值: 其中 , .18. 把下面的说理过程补充完整:
已知:如图,BC∥EF,BC=EF,AF=DC,线段AB和线段DE平行吗?请说明理由.

答:AB∥DE.
理由:
∵AF=DC(已知),
∴AF+FC=DC+ ▲ (等式的基本性质),
即:AC=DF,
∵BC∥EF(已知),
∴∠BCA=∠ ▲ ( ),
又∵BC=EF(已知),
∴△ABC≌△DEF( ),
∴∠A=∠ ▲ ( ),
∴AB∥ ▲ ( ).
19. 研究表明,当钾肥和磷肥的施用量一定时,土豆的产量与氮肥的施用量有如下关系:氮肥施用量/(千克/公顷)
0
34
67
101
135
202
259
336
404
471
土豆产量/(吨/公顷)
15.18
21.36
25.72
32.29
34.03
39.45
43.15
43.46
40.83
30.75
(1)、上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?(2)、当氮肥的施用量是101千克/公顷时,土豆的产量是多少?如果不施肥氮肥呢?(3)、根据表格中的数据,你认为氮肥的施用量是多少时比较适宜?说说你的理由.(4)、粗略说一说氮肥的施用量对土豆产量的影响.20. 如图,现有一个转盘被平均分成6等份,分别标有数字2、3、4、5、6、7这六个数字,转动转盘,当转盘停止时,指针指向的数字即为转出的数字,求: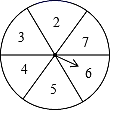 (1)、转到数字10是(从“不确定事件”“必然事件”“不可能事件”选一个填入);(2)、转动转盘,转出的数字大于3的概率是;(3)、现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.
(1)、转到数字10是(从“不确定事件”“必然事件”“不可能事件”选一个填入);(2)、转动转盘,转出的数字大于3的概率是;(3)、现有两张分别写有3和4的卡片,要随机转动转盘,转盘停止后记下转出的数字,与两张卡片上的数字分别作为三条线段的长度.①这三条线段能构成三角形的概率是多少?
②这三条线段能构成等腰三角形的概率是多少?
21. 如图,△ABC中. (1)、作边AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.(保留痕迹,不写作法)(2)、连接AD、AE,若BC=8cm,求△ADE的周长.(3)、若∠BAC=100°,求∠DAE的度数.22. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2 .
(1)、作边AB,AC的垂直平分线分别交BC于D,E两点,垂足分别是M,N.(保留痕迹,不写作法)(2)、连接AD、AE,若BC=8cm,求△ADE的周长.(3)、若∠BAC=100°,求∠DAE的度数.22. 两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2 .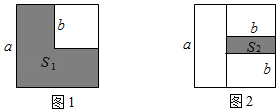 (1)、用含a,b的代数式分别表示S1、S2;(2)、若a+b=10,ab=20,求S1+S2的值.23. 综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E.
(1)、用含a,b的代数式分别表示S1、S2;(2)、若a+b=10,ab=20,求S1+S2的值.23. 综合与探究:问题情景:如图1所示,已知,在△ABC中,AC=BA,∠ACB=90°,AD是△ABC的中线,过点C作CE⊥AD,垂足为M,且交AB于点E. (1)、(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;(2)、(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;(3)、(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.
(1)、(探究一)小虎通过度量发现∠BCE=∠CAD,请你帮他说明理由;(2)、(探究二)小明在图中添加了一条线段CN,且CN平分∠ACB交AD于点N,如图2所示,即可得CN=BE,符合题意吗?请说明理由;(3)、(探究三)小刚在(2)的基础上,连接DE,如图3所示,又发现了一组全等三角形,你能发现吗?请找出来,并说明理由.