山东省临沂市河东区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各数中，是无理数的是（）

A、3.1415 B、 $\sqrt{4}$ C、 $\frac{22}{7}$ D、 $\sqrt{6}$

查看试题解析
2. 如图，直线a、b相交于点O，若∠1＝30°，则∠2等于（）

A、60° B、30° C、140° D、150°

查看试题解析
3. 在某个电影院里，如果用（2，15）表示2排15号，那么5排9号可以表示为（　　）

A、（2，15） B、（2，5） C、（5，9） D、（9，5）

查看试题解析
4. 如图，∠1和∠2是同位角的是（　　）

A、 B、 C、 D、

查看试题解析
5. 如图，将木条a，b与c钉在一起，∠1＝85°，∠2＝50°，要使木条a与b平行，木条a旋转的度数至少是（）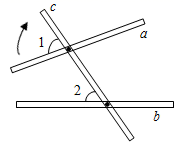

A、15° B、25° C、35° D、50°

查看试题解析
6. 已知点A在第二象限，到 x轴的距离是5，到y轴的距离是6，点A的坐标为（）

A、 $(- 5 ， 6)$ B、 $(- 6 ， 5)$ C、 $(5 ， - 6)$ D、 $(6 ， - 5)$

查看试题解析
7. 已知 $\sqrt{a - 2020}$ + $| b + 2021 |$ =0，则 $\sqrt{（ a + b ）^{2}}$ 的值为（）

A、0 B、2021 C、-1 D、1

查看试题解析
8. 给出以下命题：①对顶角相等；②在同一平面内，垂直于同一条直线的两条直线平行；③相等的角是对顶角；④内错角相等．其中假命题有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 为了了解某校3000名学生的体重情况，从中抽取了200名学生的体重，就这个问题来说，下列说法正确的是（）

A、3000名学生是总体 B、3000名学生的体重是总体 C、每个学生是个体 D、200名学生是所抽取的一个样本

查看试题解析
10. 不等式3（1﹣x）＞2﹣4x的解在数轴上表示正确的是（）

A、 B、 C、 D、

查看试题解析
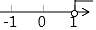11. 若点P（a-3，a-1）是第二象限内的一点，则a的取值范围是（）

A、 $a > 3$ B、 $a < 3$ C、 $a > 1$ D、 $1 < a < 3$

查看试题解析

12. 一道来自课本的习题：

从甲地到乙地有一段上坡与一段平路，如果保持上坡每小时走3km，平路每小时走4km，下坡每小时走5km，那么从甲地到乙地需54min，从乙地到甲地需42min，甲地到乙地全程是多少？

小红将这个实际问题转化为二元一次方程组问题，设未知数x，y，已经列出一个方程 $\frac{x}{3} + \frac{y}{4} = \frac{54}{60}$ ，则另一个方程正确的是（）

A、

\frac{x}{4} + \frac{y}{3} = \frac{42}{60}

B、

\frac{x}{5} + \frac{y}{4} = \frac{42}{60}

C、

\frac{x}{4} + \frac{y}{5} = \frac{42}{60}

D、

\frac{x}{3} + \frac{y}{4} = \frac{42}{60}

查看试题解析

13.
小明在拼图时，发现8个一样大小的长方形，恰好可以拼成一个大的长方形如图（1）；小红看见了，说：“我也来试一试．”结果小红七拼八凑，拼成了如图（2）那样的正方形，中间还留下了一个洞，恰好是边长为3mm的小正方形，则每个小长方形的面积为（　　）

A、120mm² B、135mm² C、108mm² D、96mm²

查看试题解析
14. 已知关于 $x ， y$ 的方程组 ${\begin{matrix} x + y = 2 + a \\ x - y = 3 a - 6 \end{matrix}$ ，给出下列结论：①当 $x ， y$ 互为相反数时， $a = - 2$ ；②当 $a = - 5$ 时解得 $x$ 为 $y$ 的2倍；③不论 $a$ 取什么实数， $x + 2 y$ 的值始终不变；④使 $x ， y$ 为自然数的 $a$ 的值共有4个．上述结论正确的有（）

A、①③ B、②④ C、①②③ D、①③④

查看试题解析

二、填空题

15. 若x＜y，且（m﹣2）x＞（m﹣2）y，则m的取值范围是．

查看试题解析
16. 已知 ${\begin{cases} x = 1 \\ y = \frac{1}{2} \end{cases}$ 是方程ax+4y＝2的一个解，那么a＝．

查看试题解析
17. 如图，直线 $A B$ 、 $C D$ 相交于点 $O$ ， $O E ⊥ A B$ ，垂足为点 $O$ ， $∠ C O E ： ∠ B O D = 2 ： 3$ ，则 $∠ A O D =$ .

查看试题解析
18. 如图，将△ABC向左平移3cm得到△DEF，AB、DF交于点G，如果△ABC的周长是12cm，那么△ADG与△BGF的周长之和是．

查看试题解析
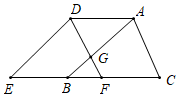19. 关于x的方程组 ${\begin{array}{l} 3 x + 2 y = 2 m + 1 \\ 2 x + 3 y = m - 1 \end{array}$ 的解满足 $x > y$ ，则m的取值范围是.

查看试题解析
20. 我们规定一种新运算，对于实数a，b，c，d，有 $| \begin{matrix} a & b \\ c & d \end{matrix} |$ =ad-bc．若正整数x满足 $| \begin{matrix} x + 2 & 2 x - 1 \\ 2 & - 3 \end{matrix} |$ ≥-18，则满足条件的x的值为．

查看试题解析

三、解答题

21.

(1)、解方程组 ${\begin{array}{l} x - y = 4 \\ 2 x + y = - 1 \end{array}$ ；

(2)、解不等式组 ${\begin{array}{l} 1 + x > 0 \\ 2 x - 6 < 0 \end{array}$ ，求出其正整数解．

查看试题解析
22. 如图，已知 $∠ A E D = ∠ C$ ， $∠ D E F = ∠ B$ ，求证： $∠ 1 = ∠ 2$ ．

请补充证明过程，并在括号内填上相应的理由．

证明： $∵ ∠ A E D = ∠ C$ （已知），

$∴$    ▲    $//$    ▲    （   ▲    ）．

$∴ ∠ B + ∠ B D E = 180 °$ （   ▲    ）．

$∵ ∠ D E F = ∠ B$ （已知），

$∴ ∠ D E F + ∠ B D E = 180 °$ （   ▲    ）．

$∴ A B // E F$ （   ▲    ）．

$∴ ∠ 1 = ∠ 2$ （   ▲    ）．

查看试题解析
23. 某校为响应国家“立德树人”的号召，鼓励学生用行动感恩父母，积极参与家务劳动，并根据学生做家务的时间来评价他们的表现．学校随机抽查了部分学生在某一周中做家务的时间，并将统计的时间（单位：小时）分成5组：A.0.5≤x<1；B.1≤x<1.5；C． 1.5≤x<2；D.2≤x<2.5；E.2.5≤x<3．制成两幅不完整的统计图：

请根据图中提供的信息，解答下列问题：

(1)、学校抽查的学生人数是人，扇形图中的m= %，补全直方图；

(2)、扇形统计图中A对应的圆心角的度数是度；

(3)、该校有800名学生，请估计这所学校学生做家务时间少于2小时的人数．

查看试题解析
24. 如图在平面直角坐标系中，已知点A（﹣1，2），B（3，4）．

(1)、画出△ABO向上平移2个单位，再向左平移4个单位后所得的图形△A′B′O′；

(2)、写出A、B、O后的对应点A′、B′、O′的坐标；

(3)、求两次平移过程中OB共扫过的面积．

查看试题解析
25. 某中学为了庆祝“建党一百周年”，计划举行阳光体育运动比赛，决定让各班购买跳绳和毽子作为活动器材．已知购买2根跳绳和5个毽子共需32元；购买4根跳绳和3个毽子共需36元．

(1)、求购买一根跳绳和一个毽子分别需要多少元？

(2)、某班需要购买跳绳和毽子的总数量是54，且购买的总费用不能超过260元；若要求购买跳绳的数量多于20根，通过计算说明共有哪几种购买跳绳的方案．

查看试题解析
26. 在综合与实践课上，老师计同学们以“两条平行线AB，CD和一块含60°角的直角三角尺EFG（∠EFG=90°，∠EGF=60°）”为主题开展数学活动．°

(1)、如图（1），若三角尺的60°角的顶点G放在CD上，若∠2 = 2∠1，求∠1的度数；

(2)、如图（2），小颖把三角尺的两个锐角的顶点E、G分别放在AB和CD上，请你探索并说明 ∠AEF与∠FGC间的数量关系；

(3)、如图（3），小亮把三角尺的直角顶点F放在CD上，30°角的顶点E落在AB上．若∠AEG=α，∠CFG=β，则∠AEG与∠CFG的数量关系是什么？用含α，β的式子表示．

查看试题解析