山东省聊城市莘县2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1. 下列方程组中,属于二元一次方程组的是( )A、 B、 C、 D、2. 如图,现要从村庄A修建一条连接公路PQ的最短小路,过点A作AH⊥PQ于点H,沿AH修建公路,则这样做的理由是( )
 A、两点之间,线段最短 B、垂线段最短 C、过一点可以作无数条直线 D、两点确定一条直线3. 下列运算正确的是( )A、m2+2m=3m3 B、m4÷m2=m2 C、m2•m3=m6 D、( m2)3=m54. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α与∠β一定相等的图形个数共有( )
A、两点之间,线段最短 B、垂线段最短 C、过一点可以作无数条直线 D、两点确定一条直线3. 下列运算正确的是( )A、m2+2m=3m3 B、m4÷m2=m2 C、m2•m3=m6 D、( m2)3=m54. 如图,一副三角尺按不同的位置摆放,摆放位置中∠α与∠β一定相等的图形个数共有( ) A、1个 B、2个 C、3个 D、4个5. 如图,∠1和∠2不是同位角的是( )A、
A、1个 B、2个 C、3个 D、4个5. 如图,∠1和∠2不是同位角的是( )A、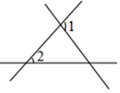 B、
B、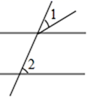 C、
C、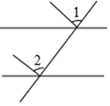 D、
D、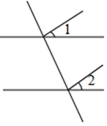 6. 若方程组 的解满足 ,则 的值为( )A、 B、1 C、0 D、不能确定7. 若 , ,则 等于( )A、 B、 C、 D、8. 如图,在△ABC中,已知点D、E、F分别是BC、AD、CE的中点,且△ABC的面积为16,则△BEF的面积是( )
6. 若方程组 的解满足 ,则 的值为( )A、 B、1 C、0 D、不能确定7. 若 , ,则 等于( )A、 B、 C、 D、8. 如图,在△ABC中,已知点D、E、F分别是BC、AD、CE的中点,且△ABC的面积为16,则△BEF的面积是( )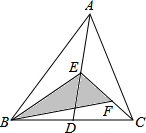 A、2 B、4 C、6 D、89. 已知△ABC的边长分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是( )A、2a B、﹣2b C、2a+3b D、2b﹣2c10. 已知a﹣b=2,ab=1,则(a+b)2的值为( )A、6 B、8 C、10 D、1211. 如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若∠BFE=3∠BFH,∠BFH=20°,则∠GFH的度数是( )
A、2 B、4 C、6 D、89. 已知△ABC的边长分别为a,b,c,化简|a+b﹣c|﹣|b﹣a﹣c|的结果是( )A、2a B、﹣2b C、2a+3b D、2b﹣2c10. 已知a﹣b=2,ab=1,则(a+b)2的值为( )A、6 B、8 C、10 D、1211. 如图,将长方形纸片ABCD的∠C沿着GF折叠(点F在BC上,不与B,C重合),使点C落在长方形内部点E处,若∠BFE=3∠BFH,∠BFH=20°,则∠GFH的度数是( )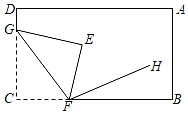 A、85° B、90° C、95° D、100°12. 如图,某渔船正在海上 处捕鱼,计划先向北偏东30°的方向航行10千米到 处,然后右转40°再航行10千米到 处,若渔船直接从 处航行到 处,航行的中线应该是( )
A、85° B、90° C、95° D、100°12. 如图,某渔船正在海上 处捕鱼,计划先向北偏东30°的方向航行10千米到 处,然后右转40°再航行10千米到 处,若渔船直接从 处航行到 处,航行的中线应该是( )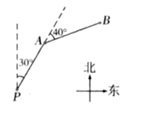 A、北偏东10° B、北偏茫40° C、北偏东50° D、北偏东70°
A、北偏东10° B、北偏茫40° C、北偏东50° D、北偏东70°二、填空题
-
13. 国产手机芯片麒麟980是全球首个7纳米制程芯片,已知1纳米=0.000 000 001米,将7纳米用科学记数法表示为米.14. 若 是关于x的完全平方式,则m= .15. 甲、乙两人共同解方程组 ,由于甲看错了方程①中的a,得到方程组的解为 ,乙看错了方程②中的b,得到方程组的解为 ,则a2020+ ( )2021= .16. 已知 轴,点 的坐标为 并且 ,则点 的坐标为 .17. 为了求1+2+22+23+…+2100的值,可令S=1+2+22+23+…+2100 , 则2S=2+22+23+24+…+2101 , 因此2S﹣S=2101﹣1,所以S=2101﹣1,即1+2+22+23+…+2100=2101﹣1,仿照以上推理计算1+3+32+…+3100的值是 .
三、解答题
-
18. 解方程组(1)、(2)、 .19. 把下列各式因式分解:(1)、 ;(2)、 .20. 两条直线被第三条直线所截,∠1是∠2的同旁内角,∠2是∠3的内错角.(1)、画出示意图,标出∠1,∠2,∠3;(2)、若∠1=2∠2,∠2=2∠3, 求∠1,∠2,∠3 的度数.21. 计算.(1)、3a3b•(﹣2ab)+(﹣3a2b)2 .(2)、x(x﹣1)﹣(x+1)(x﹣2);(3)、 .22.(1)、已知x2﹣2x=2,将下式先化简,再求值:(x﹣1)2+(x﹣3)+(x+3)+(x﹣3)(x﹣1);(2)、已知a、b、c是△ABC的三边的长,若满足a2+2b2+c2﹣2b(a+c)=0,试判断此三角形的形状.23. 已知在平面直角坐标系中有三点 、 、 ,请回答如下问题:
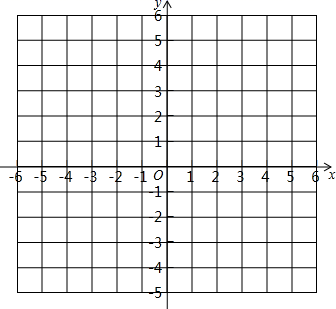 (1)、在坐标系内描出点 的位置:(2)、求出以 三点为顶点的三角形的面积;(3)、在 轴上是否存在点 ,使以 三点为顶点的三角形的面积为10,若存在,请直接写出点 的坐标;若不存在,请说明理由.
(1)、在坐标系内描出点 的位置:(2)、求出以 三点为顶点的三角形的面积;(3)、在 轴上是否存在点 ,使以 三点为顶点的三角形的面积为10,若存在,请直接写出点 的坐标;若不存在,请说明理由.