山东省济宁市金乡县2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程中：① $x y = 1$ ；② $3 x + \frac{2}{y} = 4$ ；③ $2 x + 3 y = 0$ ；④ $\frac{x}{4} + \frac{y}{3} = 7$ ，二元一次方程有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 下列实数： $\frac{π}{3}$ ， $\sqrt{9}$ ， $\sqrt[3]{- 6}$ ， $\frac{22}{7}$ ，0.1010010001…（两个1之间依次增加一个0）．无理数的个数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
3. 在“12•4中国国家宪法日”来临之际，金乡某社区为了解该社区居民的法律意识，随机调查测试了该社区1000人，其中有980人的法律意识测试结果为合格及以上．关于以上数据的收集与整理过程，下列说法正确的是（）

A、调查的方式是抽样调查 B、1000人的法律意识测试结果是总体 C、该社区只有20人的法律意识不合格 D、样本是980人

查看试题解析
4. 若关于 $x$ 的一元一次不等式组 ${\begin{array}{l} x - a \geq 0 ， \\ 2 x + 1 > 3 \end{array}$ 的解集为 $x > 1$ ，则 $a$ 的取值范围是（）

A、 $a < 1$ B、 $a \leq 1$ C、 $a > 1$ D、 $a \geq 1$

查看试题解析
5. 已知点P（1﹣a，2a+6）在第四象限，则a的取值范围是（）

A、a＜﹣3 B、﹣3＜a＜1 C、a＞﹣3 D、a＞1

查看试题解析
6. 如图，从① $∠ 1 = ∠ 2$ ，② $∠ C = ∠ D$ ，③ $D F // A C$ 三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为（）

A、0 B、1 C、2 D、3

查看试题解析
7. 某球队参加比赛，开局11场保持不败，积23分，按比赛规则，胜一场得3分，平一场得1分，则该队获胜的场数为（）

A、4 B、5 C、6 D、7

查看试题解析
8. 在长方形 $A B C D$ 中，放入6个形状大小完全相同的小长方形，所标尺寸如图所示，则小长方形的宽 $A E$ 的长度为（） cm .

A、1 B、1.6 C、2 D、2.5

查看试题解析
9. 已知 $\min {a ， b ， c}$ 表示取三个数中最小的那个数．例如：当 $x = - 2$ 时， $\min {| - 2 | ， {(- 2)}^{2} ， {(- 2)}^{3}} = - 8$ ，当 $\min {\sqrt{x} ， x^{2} ， x} = \frac{1}{16}$ 时，则 $x$ 的值为（）

A、 $\frac{1}{16}$ B、 $\frac{1}{8}$ C、 $\frac{1}{4}$ D、 $\frac{1}{2}$

查看试题解析
10. 如图， $∠ B A C = ∠ A C D = 90 °$ ， $∠ A B C = ∠ A D C$ ， $C E ⊥ A D$ ，且 $B E$ 平分 $∠ A B C$ ，则下列结论：① $A D / / C B$ ；② $∠ A C E = ∠ A B C$ ；③ $∠ E C D + ∠ E B C = ∠ B E C$ ；④ $∠ C E F = ∠ C F E$ ；其中正确的是（）

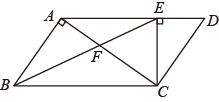A、①② B、①③④ C、①②④ D、①②③④

查看试题解析

二、填空题

11. 已知实数a+b的算术平方根是2，实数 $\frac{1}{3}$ a的立方根是﹣1，则b﹣3a的平方根为．

查看试题解析
12. 将含30°角的一个直角三角板和一把直尺（两边a $//$ b）如图放置，若∠1＝50°，则∠2的度数为．

查看试题解析
13. 在平面直角坐标系中，点 $P (m - 3 ， 4 - 2 m)$ 不可能在第象限．

查看试题解析
14. 已知不等式组 ${\begin{array}{l} x + 2 > 1 \\ x - 1 < m - 1 \end{array}$ 的解集中只有三个整数解，则 $m$ 的范围是．

查看试题解析
15. 已知关于x，y的方程组 ${\begin{matrix} 2 x - 4 y = a - 1 \\ x + 2 y = 2 a - 1 \end{matrix}$ 与方程3x﹣y＝8的解相同，则a²+2a＝．

查看试题解析

三、解答题

16.

(1)、计算： $- {(- 1)}^{2018} - | 2 - \sqrt{3} | + \sqrt{81} + \sqrt[3]{- 27}$

(2)、解方程组 ${\begin{matrix} x + 2 y = 3 \\ \frac{x}{2} - \frac{2 + y}{3} = - \frac{1}{2} \end{matrix}$ ．

查看试题解析
17. 解不等式组： ${\begin{array}{l} 3 (x + 2) > x - 2 \\ x - \frac{2}{3} \leq \frac{1 + x}{2} \end{array}$ 并将解集在数轴上表示出来．

查看试题解析
18. 已知，如图，把三角形ABC向上平移4个单位长度，再向右平移3个单位长度，得到三角形A′B′C′，其中点A′，B′，C′分别为点A，B，C的对应点．

(1)、画出三角形A′B′C′，并直接写出C′的坐标；

(2)、若AB边上一点P经过上述平移后的对应点为P′（x，y）．直接写出用含x，y的式子表示点P的坐标（，）；

(3)、一般地，将一个图形依次沿两个坐标轴方向平移所得到的图形，可以通过原来的图形作一次平移得到，求线段BC在一次平移过程中扫过的面积．

查看试题解析
19. 如图，已知 $A B // C D$ ，∠B=∠D，AE交BC的延长线于点E.

(1)、求证： $A D // B E$ ；

(2)、若∠1=∠2=60°，∠BAC=2∠EAC，求∠DCE的度数.

查看试题解析

20. “触发青春灵感，科技点亮生活”，某中学举行了知识竞赛，为了解此次知识竞赛成绩的情况，随机抽取了部分参赛学生的成绩，整理并制作出如下的不完整的统计表和统计图，如图所示．

组别	成绩x/分	频数
A组	$60 \leq x < 70$	a
B组	$70 \leq x < 80$	8
C组	$80 \leq x < 90$	12
D组	$90 \leq x < 100$	14

请根据图表信息解答以下问题

(1)、a= ，一共抽取了个参赛学生的成绩；

(2)、补全频数分布直方图；

(3)、计算扇形统计图中“B”与“C”对应的圆心角度数；

(4)、若学校为成绩在80分以上（包括80分）的学生颁发优秀证书，则抽取学生成绩为“优秀”的人数占所抽取学生的百分比是多少？

查看试题解析

21. 每年的6月5日为世界环保日，为了提倡低碳环保，某公司决定购买10台节省能源的新设备，现有甲、乙两种型号的设备可供选购. 经调查：购买3台甲型设备比购买2台乙型设备多花16万元，购买2台甲型设备比购买3台乙型设备少花6万元.

(1)、求甲、乙两种型号设备的价格；

(2)、该公司经预算决定购买节省能源的新设备的资金不超过110万元，你认为该公司有哪几种购买方案；

(3)、在（2）的条件下，已知甲型设备的产量为240吨/月，乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨，为了节约资金，请你为该公司设计一种最省钱的购买方案.

查看试题解析
22. 阅读材料并回答下列问题：当m，n都是实数，且满足2m＝8＋n，就称点P（m﹣1， $\frac{n + 2}{2}$ ）为“爱心点”．

(1)、判断点A（5，3），B（4，6）哪个点为“爱心点”，并说明理由；

(2)、若点C（a，﹣8）也是“爱心点”，请求出a的值；

(3)、已知p，q为有理数，且关于x，y的方程组 ${\begin{matrix} x + y = \sqrt{3} p + q \\ x - y = \sqrt{3} p - 3 q \end{matrix}$ 解为坐标的点B（x，y）是“爱心点”，求p，q的值．

查看试题解析