山东省德州市陵城区2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1. 下列命题中是假命题的是( )A、两点之间,线段最短 B、同旁内角互补 C、等角的补角相等 D、垂线段最短2. 为了解某中学八年级600名学生的身高情况,抽查了其中100名学生的身高进行统计分析.下面叙述正确的是( )A、以上调查属于全面调查 B、每名学生是总体的一个个体 C、100名学生的身高是总体的一个样本 D、600名学生是总体3. 如图,已知 , 平分 , ,则 为( )
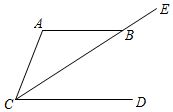 A、 B、 C、 D、4. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、5. 下列四个数:﹣2,﹣0.6, , 中,绝对值最小的是( )A、﹣2 B、﹣0.6 C、 D、6. 若方程 的解分别为 ,且 ,下列说法正确的是( )A、 是5的平方根 B、 是5的平方根 C、 是5的算术平方根 D、 是5的算术平方根7. 点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )A、(5,﹣3) B、(﹣5,3) C、(3,﹣5) D、(﹣3,5)8. 如图,给出下列条件:①∠1=∠2:②∠3=∠4:③AB∥CE,且∠ADC=∠B:④AB∥CE,且∠BCD=∠BAD.其中能推出BC∥AD的条件为( )
A、 B、 C、 D、4. 下列方程组中,是二元一次方程组的是( )A、 B、 C、 D、5. 下列四个数:﹣2,﹣0.6, , 中,绝对值最小的是( )A、﹣2 B、﹣0.6 C、 D、6. 若方程 的解分别为 ,且 ,下列说法正确的是( )A、 是5的平方根 B、 是5的平方根 C、 是5的算术平方根 D、 是5的算术平方根7. 点M在第二象限,距离x轴5个单位长度,距离y轴3个单位长度,则M点的坐标为( )A、(5,﹣3) B、(﹣5,3) C、(3,﹣5) D、(﹣3,5)8. 如图,给出下列条件:①∠1=∠2:②∠3=∠4:③AB∥CE,且∠ADC=∠B:④AB∥CE,且∠BCD=∠BAD.其中能推出BC∥AD的条件为( ) A、①② B、②④ C、②③ D、②③④9. 将点 向左平移1个单位长度到 ,且 在y轴上,那么 的坐标是( )A、 B、 C、 D、10. 若方程组 的解x与y的和为3,则a的值为( )A、7 B、4 C、0 D、-411. 在平面直角坐标系中,若点 在第四象限,则 的取值范围是( )A、 B、 C、 D、12. 在平面直角坐标系中,张敏做走棋游戏,其走法:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…,以此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n能被3除时,余数为1时,则向右走1个单位;当n能被3除时,余数为2时,则向右走2个单位,当走完67步时,棋子所处的位置坐标是( )A、(66,22) B、(66,23) C、(67,23) D、(67,22)
A、①② B、②④ C、②③ D、②③④9. 将点 向左平移1个单位长度到 ,且 在y轴上,那么 的坐标是( )A、 B、 C、 D、10. 若方程组 的解x与y的和为3,则a的值为( )A、7 B、4 C、0 D、-411. 在平面直角坐标系中,若点 在第四象限,则 的取值范围是( )A、 B、 C、 D、12. 在平面直角坐标系中,张敏做走棋游戏,其走法:棋子从原点出发,第1步向右走1个单位,第2步向右走2个单位,第3步向上走1个单位,第4步向右走1个单位…,以此类推,第n步的走法是:当n能被3整除时,则向上走1个单位;当n能被3除时,余数为1时,则向右走1个单位;当n能被3除时,余数为2时,则向右走2个单位,当走完67步时,棋子所处的位置坐标是( )A、(66,22) B、(66,23) C、(67,23) D、(67,22)二、填空题
-
13. 如图,将长方形纸片ABCD沿对角线BD折叠,点C的对应点为E . 若∠CBD=32°,则∠ADE的度数为 .
 14. 为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:
14. 为了解某一路口某一时段的汽车流量,小明同学10天中在同一时段统计通过该路口的汽车数量(单位:辆),将统计结果绘制成如下折线统计图:
由此估计一个月(30天)该时段通过该路口的汽车数量超过200辆的天数为 天.
15. 已知 是关于 的一元一次不等式,则 的值为 .16. 如图,实数a,b,c在数轴上对应点的位置如图所示,化简 +|b﹣a|﹣ ﹣|b﹣c|的结果是 . 17. 已知平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为 .18. 如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知 ,则点A的坐标为.
17. 已知平面直角坐标系内不同的两点A(3a+2,4)和B(3,2a+2)到x轴的距离相等,则a的值为 .18. 如图,5个大小形状完全相同的长方形纸片,在直角坐标系中摆成如图图案,已知 ,则点A的坐标为.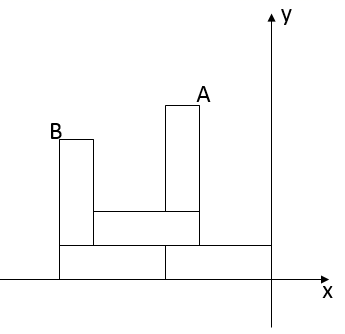
三、解答题
-
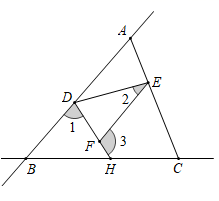
19. 计算 .20. 如图,直线 和直线 相交于点 ,连接 ,点 分别在 、 、 上,连接 、 , 是 上一点,已知
 (1)、求证: ;(2)、若 平分 , ,求 的度数.(用 表示)21. 若关于 的二元一次方程组 的解满足(1)、x-y=;x+y=(用含 m 的代数式表示);(2)、求 的取值范围.22. 为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.
(1)、求证: ;(2)、若 平分 , ,求 的度数.(用 表示)21. 若关于 的二元一次方程组 的解满足(1)、x-y=;x+y=(用含 m 的代数式表示);(2)、求 的取值范围.22. 为了解2020年全国中学生创新能力大赛中竞赛项目“知识产权”笔试情况,随机抽查了部分参赛同学的成绩,整理并制作了不完整的频数分布表.分数x(分)
频数
百分比
60≤x<70
30
10%
70≤x<80
90
n
80≤x<90
m
40%
90≤x≤100
60
20%

请根据图表提供的信息,解答下列问题:
(1)、本次调查的样本容量为;(2)、在表中:m= ;n=;(3)、根据频数分布表画频数分布直方图;(4)、如果比赛成绩在80分以上(含80分)为优秀,那么你估计参加该竞赛项目的的30000人中,优秀人数大约是 .23. 学校为表彰在“了不起我的国”演讲比赛中获奖的选手,决定购买甲、乙两种图书作为奖品.已知购买30本甲种图书,50本乙种图书共需1350元;购买50本甲种图书,30本乙种图书共需1450元.(1)、求甲、乙两种图书的单价分别是多少元?(2)、学校要求购买甲、乙两种图书共40本,且甲种图书的数量不少于乙种图书数量的 ,请设计最省钱的购书方案.24. 平面直角坐标系中, 为原点,点 , , .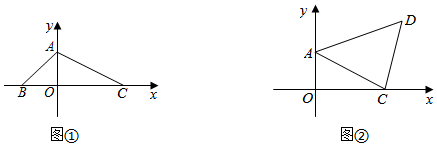 (1)、如图①,则三角形 的面积为;(2)、如图②,将点 向右平移7个单位长度,再向上平移4个单位长度,得到对应点 .
(1)、如图①,则三角形 的面积为;(2)、如图②,将点 向右平移7个单位长度,再向上平移4个单位长度,得到对应点 .①求 的面积;
②点 是一动点,若三角形 的面积等于三角形 的面积.请直接写出点 坐标.
25. 对x,y定义一种新运算T,规定:T(x,y)=ax+2by﹣1(其中a、b均为非零常数),这里等式右边是通常的四则运算,例如:T(0,1)=a•0+2b•1﹣1=2b﹣1.(1)、已知T(1,﹣1)=﹣2,T(4,2)=3.①求a,b的值;
②若关于m的不等式组 恰好有2个整数解,求实数p的取值范围;
(2)、若T(x,y)=T(y,x)对任意实数x,y都成立(这里T(x,y)和T(y,x)均有意义),则a,b应满足怎样的关系式?