山东省德州市临邑县2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1. 在下列实数 ,3.14159265, ,﹣8, , , 中无理数有( )A、3个 B、4个 C、5个 D、6个2. 为了了解全校七年级300名学生的视力情况,李老师从中抽查了50名学生的视力情况.针对这个问题,下面说法正确的是( ).A、300名学生是总体 B、每名学生是个体 C、50名学生是所抽取的一个样本 D、这个样本容量是503. 下列四个命题:①对顶角相等;②内错角相等;③平行于同一条直线的两条直线互相平行;④如果一个角的两边分别平行于另一个角的两边,那么这两个角相等;⑤过一点有且只有一条直线与已知直线垂直.其中真命题的个数是( )A、1个 B、2个 C、3个 D、4个4. 下列各式中,正确的是( )A、 B、 C、 D、5. 下列命题是真命题的是( )A、如果两个角不相等,那么这两个角不是对顶角; B、两互补的角一定是邻补角 C、如果a2=b2 , 那么a=b; D、如果两角是同位角,那么这两角一定相等6. 如图,下列能判定 的条件有( )个.
⑴ ;⑵ ;⑶ ;⑷ .
 A、1 B、2 C、3 D、47. 不等式 的解集是 ,则m的取值范围是( )A、 B、 C、 D、8. 已知:直线 ,一块含 角的直角三角板如右图所示放置,∠1=25°,∠2等于( )
A、1 B、2 C、3 D、47. 不等式 的解集是 ,则m的取值范围是( )A、 B、 C、 D、8. 已知:直线 ,一块含 角的直角三角板如右图所示放置,∠1=25°,∠2等于( ) A、 B、 C、 D、9. 已知方程组 的解满足 ,则k的值为( )A、4 B、 C、2 D、10. 某中学七年级一班40名同学为灾区捐款,共捐款2000元,捐款情况如下表:
A、 B、 C、 D、9. 已知方程组 的解满足 ,则k的值为( )A、4 B、 C、2 D、10. 某中学七年级一班40名同学为灾区捐款,共捐款2000元,捐款情况如下表:捐款(元)
20
40
50
100
人数
10
8
由于疏忽,表格中捐款40元和50元的人数忘记填写了,若设捐款40元的有x名同学,捐款50元的有y名同学,根据题意,可得方程组( )
A、 B、 C、 D、11. 若方程mx+ny=6的两个解是 , ,则m,n的值为( )A、4,2 B、2,4 C、﹣4,﹣2 D、﹣2,﹣412. 在平面直角坐标系中,一个智能机器人接到如下指令:从原点O出发,按向右,向上,向右,向下的方向依次不断移动,每次移动 .其行走路线如图所示,第1次移动到 ,第2次移动到 ,…,第n次移动到 ,则 的面积是( )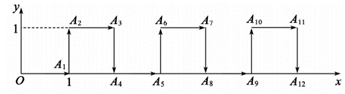 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 的平方根是 .14. 若点(m﹣4,1﹣2m)在第三象限内,则m的取值范围是 .15. 如图,将周长为14的三角形 向右平移1个单位后得到三角形 ,则四边形 的周长等于 .
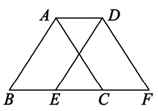 16. “已知关于 的不等式组 的整数解共有3个,则m的取值范围是。17. 如图,已知 .
16. “已知关于 的不等式组 的整数解共有3个,则m的取值范围是。17. 如图,已知 . 18. 在平面直角坐标系中,四边形ABCD四个顶点分别是A(−4,−4),B(1,−4),C(1,−2),D(−4,−2).设点M是四边形ABCD边上的动点,直线AM将四边形ABCD的周长分为3:4两部分,则点M的坐标是 .
18. 在平面直角坐标系中,四边形ABCD四个顶点分别是A(−4,−4),B(1,−4),C(1,−2),D(−4,−2).设点M是四边形ABCD边上的动点,直线AM将四边形ABCD的周长分为3:4两部分,则点M的坐标是 .三、解答题
-
19. 为响应国家要求中小学生每天锻炼1小时的号召,某校开展了形式多样的“阳光体育运动”活动,小明对某班同学参加锻炼的情况进行了统计,并绘制了下面的图1和图2.
 (1)、该班共有多少名学生?若全年级共有1200名学生,估计全年级参加乒乓球活动的学生有多少名?(2)、请在图1中将“乒乓球”部分的图形补充完整,并求出扇形统计图中,表示“足球”的扇形圆心角的度数.20. 解方程组:(1)、 ,(2)、21. 解不等式组:并把它的解集在数轴上表示出来.(1)、
(1)、该班共有多少名学生?若全年级共有1200名学生,估计全年级参加乒乓球活动的学生有多少名?(2)、请在图1中将“乒乓球”部分的图形补充完整,并求出扇形统计图中,表示“足球”的扇形圆心角的度数.20. 解方程组:(1)、 ,(2)、21. 解不等式组:并把它的解集在数轴上表示出来.(1)、 (2)、
(2)、 22. 如图,将三角形 向右平移2个单位长度再向下平移3个单位长度,得到对应的三角形 .
22. 如图,将三角形 向右平移2个单位长度再向下平移3个单位长度,得到对应的三角形 . (1)、分别写出点A、B、C的坐标.(2)、画出三角形 ,并分别写出点 的坐标.(3)、求三角形 的面积.23. 填写推理理由
(1)、分别写出点A、B、C的坐标.(2)、画出三角形 ,并分别写出点 的坐标.(3)、求三角形 的面积.23. 填写推理理由
如图,已知 ,
求证: .
理由如下:
∵ ( ),且 ( ),
∴ (等量代换),
∴ ( )
∴ ( )
又∵ (已知),
∴ (等量代换),
∴ ( )
24. 去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.(1)、求饮用水和蔬菜各有多少件?(2)、现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;(3)、在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?25. 如图,直线 , ,E、F在 上,且满足 , 平分(1)、求 的度数; (2)、若平行移动 ,那么 的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)、在平行移动 的过程中,是否存在某种情况,使 ?若存在,求出 度数;若不存在,说明理由.
(2)、若平行移动 ,那么 的值是否随之发生变化?若变化,找出变化规律或求出变化范围;若不变,求出这个比值.(3)、在平行移动 的过程中,是否存在某种情况,使 ?若存在,求出 度数;若不存在,说明理由.