内蒙古自治区乌海市海勃湾区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 在下列实数： $\frac{π}{2}$ 、 $\sqrt{3}$ 、 $\sqrt{4}$ 、 $\frac{22}{7}$ 、 $- 1.010010001$ …（相连两个1之间依次多一个0）中，无理数有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
2. 甲种蔬菜保鲜适宜的温度是1℃~5℃，乙种蔬菜保鲜适宜的温度是3℃~8℃，将这两种蔬菜放在一起同时保鲜，适宜的温度是（）

A、1℃~3℃ B、3℃~5℃ C、5℃~8℃ D、1℃~8℃

查看试题解析
3. 如图，直线 $a / / b$ ，等腰直角三角形的两个顶点分别落在直线 $a$ 、 $b$ 上，若 $∠ 1 = 30^{\circ}$ ，则 $∠ 2$ 的度数是（）

A、 $45^{\circ}$ B、 $30^{\circ}$ C、 $15^{\circ}$ D、 $10^{\circ}$

查看试题解析
4. 如图，数轴上的点A，B，O，C，D分别表示数-2，-1，0，1，2，则表示数 $2 - \sqrt{5}$ 的点P应落在 $($ $)$

A、线段AB上 B、线段BO上 C、线段OC上 D、线段CD上

查看试题解析
5. 若 $a < b$ ，则下列结论不一定成立的是（）

A、 $1 - a > 1 - b$ B、 $2 a < 2 b$ C、 $- \frac{a}{3} > - \frac{b}{3}$ D、 $a^{2} < b^{2}$

查看试题解析
6. 下列命题中，①过一点有且只有一条直线与已知直线平行；②直角的补角是直角；③若点C（x，y）满足 $x y > 0$ ，则点C在第一象限；④负数没有立方根．真命题的个数是（）

A、3 B、4 C、2 D、1

查看试题解析
7. 下列调查中：
①检测保定的空气质量；②了解《奔跑吧，兄弟》节日收视率的情况；③保证“神舟九号“成功发射，对其零部件进行检查；④调查某班50名同学的视力情况；⑤了解一沓钞票中有没有假钞

其中通合采用抽样调查的是（）

A、①②③ B、①② C、①③⑤ D、②④

查看试题解析
8. 一个正数的两个平方根分别是2a-1与-a+2，则a的值为（）

A、1 B、-1 C、2 D、-2

查看试题解析
9. 如图，周长为34的矩形ABCD被分成7个全等的矩形，则矩形ABCD的面积为（）

A、60 B、52 C、70 D、66

查看试题解析
10. 点P的坐标是（2-a，3a+6），且点P到两坐标轴的距离相等，则点P坐标是（）

A、（3， 3） B、（3，-3） C、（6，-6） D、（3，3）或 $(6 ， - 6)$

查看试题解析
11.
如图，从①∠1=∠2 ②∠C=∠D ③∠A=∠F 三个条件中选出两个作为已知条件，另一个作为结论所组成的命题中，正确命题的个数为（　　）

A、0 B、1 C、2 D、3

查看试题解析
12. 若关于x的不等式组 ${\begin{matrix} x < 2 (x - a) \\ x - 1 \leq \frac{2}{3} x \end{matrix}$ 恰有3个整数解，则a的取值范围是（）

A、 $0 \leq a < \frac{1}{2}$ B、 $0 < a \leq \frac{1}{2}$ C、 $- \frac{1}{2} < a \leq 0$ D、 $0 \leq a \leq \frac{1}{2}$

查看试题解析

二、填空题

13. 计算 $\sqrt{81} + | 2 - \sqrt{3} | + \sqrt[3]{- 125} + 6 \div (- \frac{3}{4})$ = ．

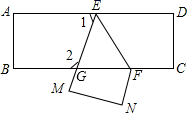
查看试题解析
14. 已知∠A=60°，∠A与∠B的两边分别互相平行，则∠B= ．

查看试题解析
15. 在平面直角坐标系中，若点 $M (1 ， 3)$ 与点 $N (x ， 3)$ 的距离是8，则 $x$ 的值是

查看试题解析
16. 若 ${(a - 2)}^{2} + \sqrt{b + 1} = 0$ ．则 $b^{a}$ ＝．

查看试题解析
17. 如图，把一张长方形纸片ABCD沿EF折叠后，D、C分别在M、N的位置上，EM与BC的交点为G，若∠EFG＝65°，则∠2＝．

查看试题解析
18. 如图所示，将直角三角形ABC沿 $B C$ 方向平移得到直角三角形DEF，如果AB＝12cm，BE＝5cm，DH＝4cm，则图中阴影部分面积为cm².

查看试题解析
19. 若关于x、y的二元一次方程组 ${\begin{matrix} 3 x + m y = 16 \\ 2 x + n y = 15 \end{matrix}$ 的解是 ${\begin{matrix} x = 7 \\ y = 3 \end{matrix}$ ，则关于x、y的二元一次方程组 ${\begin{matrix} 3 (x + y) + m (x - y) = 16 \\ 2 (x + y) + n (x - y) = 15 \end{matrix}$ 的解是．

查看试题解析
20. 杨辉是中国南宋末年的一位杰出的数学家．在他著的《详解九章算法》一书中，画了一张表示二项式展开后的系数构成的三角图形，称作“开方作法本源”，现在简称为“杨辉三角”，它是杨辉的一大重要研究成果，观察每行数的和，并归纳出第n行数的和为．

查看试题解析

三、解答题

21.

(1)、解方程组 ${\begin{matrix} 3 (x + y) - 4 (x - y) = 4 \\ \frac{x + y}{2} + \frac{x - y}{6} = 1 \end{matrix}$ ；

(2)、解不等式组 ${\begin{matrix} 2 - x > 0 \\ \frac{5 x + 1}{2} + 1 \geq \frac{2 x - 1}{3} \end{matrix}$ ．

查看试题解析
22. 某校为了解本校1200名初中生对安全知识掌握情况，随机抽取了60名初中生进行安全知识测试，并将测试成绩进行统计分析，绘制了如下不完整的频数统计表和频数直方图：

请结合图表完成下列各题：

(1)、频数表中的a＝， b＝；

(2)、将频数分布直方图补充完整；

(3)、若测试成绩不低于80分定为“优秀”，你估计该校的初中生对安全知识掌握情况为“优秀”等级的大约有多少人？

查看试题解析
23. 如图，已知 $A (- 4 ， - 1)$ ， $B (- 5 ， - 4)$ ， $C (- 1 ， - 3)$ ， $△ A B C$ 经过平移得到的 $△ A^{'} B^{'} C^{'}$ ， $△ A B C$ 中任意一点 $P (x_{1} ， y_{1})$ 平移后的对应点为 $P^{'} (x_{1} + 6 ， y_{1} + 4)$ .

(1)、求出点 $A^{'}$ ， $B^{'}$ ， $C^{'}$ 的坐标；

(2)、请在图中作出 $△ A^{'} B^{'} C^{'}$ ；

(3)、求 $△ A B C$ 的面积.

查看试题解析
24. 如图，已知∠1=∠2，∠3=∠4，∠5=∠A，试说明：BE∥CF．
完善下面的解答过程，并填写理由或数学式：

解：∵∠3=∠4（已知）

∴AE∥    ▲    （    ▲    ）

∴∠EDC=∠5（    ▲    ）

∵∠5=∠A（已知）

∴∠EDC=    ▲    （    ▲    ）

∴DC∥AB（    ▲    ）

∴∠5+∠ABC=180°（    ▲    ）

即∠5+∠2+∠3=180°

∵∠1=∠2（已知）

∴∠5+∠1+∠3=180°（    ▲    ）

即∠BCF+∠3=180°

∴BE∥CF（    ▲    ）．

查看试题解析
25. 为响应市政府“创建国家森林城市”的号召，某小区计划购进A、B两种树苗共17棵．若购进1棵A种树苗与2棵B种树苗共需200元；购进2棵A种树苗与1棵B种树苗共需220元．

(1)、求购进A种树苗和B种树苗每棵各多少元？

(2)、若购进B种树苗的数量少于A种树苗的数量，且总费用不超过1200元，则A、B两种树苗各购进多少棵？

查看试题解析
26. 如图，在平面直角坐标系中，点O为坐标原点，三角形OAB的边OA、OB分别在x轴正半轴上和y轴正半轴上，A（a，0），a是方程 $\frac{a + 2}{3} - \frac{a - 2}{2} = 1$ 的解，且△OAB的面积为6．

(1)、求点A、B的坐标；

(2)、将线段OA沿轴向上平移后得到PQ，点O、A的对应点分别为点P和点Q（点P与点B不重合），设点P的纵坐标为t，△BPQ的面积为S，请用含t的式子表示S；

(3)、在（2）的条件下，设PQ交线段AB于点K，若PK= $\frac{8}{3}$ ，求t的值及△BPQ的面积．

查看试题解析