吉林省长春市双阳区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 方程x﹣2=2﹣x的解是（　　）

A、x=1 B、x=﹣1 C、x=2 D、x=0

查看试题解析
2. 方程4x﹣y＝8，xy＝2，x $+ \frac{3}{y} =$ 3，3﹣2y＝z，x²+y＝6中二元一次方程的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
3. 若有理数a、b满足a＞b，则下列结论正确的是（）

A、a+2＜b+2 B、﹣a﹣1＞﹣b﹣1 C、3a＞3b D、 $\frac{a}{2} < \frac{b}{2}$

查看试题解析
4. 按如图所示的运算程序，使输出结果为1的x、y的值是（）

A、 ${\begin{matrix} x = 1 \\ y = 1 \end{matrix}$ B、 ${\begin{matrix} x = 1 \\ y = 2 \end{matrix}$ C、 ${\begin{matrix} x = 2 \\ y = 1 \end{matrix}$ D、 ${\begin{matrix} x = 2 \\ y = 2 \end{matrix}$

查看试题解析
5. 下列四个图中，正确画出△ABC中BC边上的高是（）

A、 B、 C、 D、

查看试题解析
6. 下列正多边形中，能够铺满地面的是（）

A、正五边形 B、正六边形 C、正八边形 D、正十二边形

查看试题解析
7. 下列图形中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
8. 如图，一个倾斜的天平两边分别放有2个小立方体和3个砝码，每个砝码的质量都是5克，每个小立方体的质量都是m克，则m的取值范围是（）

A、m＜15 B、m＞15 C、m $> \frac{15}{2}$ D、m $< \frac{15}{2}$

查看试题解析
9. 如图，将四边形ABCD去掉一个80°的角得到一个五边形BCDEF，则∠1与∠2的和为（）

A、240° B、260° C、280° D、300°

查看试题解析
10. 当三角形中一个内角β是另外一个内角α的 $\frac{1}{2}$ 时，我们称此三角形为“友好三角形”．如果一个“友好三角形”中有一个内角为54°，那么这个“友好三角形”的“友好角α”的度数为（）

A、108°或27° B、108°或54° C、27°或54°或108° D、54°或84°或108°

查看试题解析

二、填空题

11. 已知关于x的一元一次方程2x+m＝1的解是x＝1，则m的值为．

查看试题解析
12. 已知二元一次方程3x﹣2y＝5，用含x的代数式表示y为．

查看试题解析
13. 不等式1﹣2x＜6的负整数解是．

查看试题解析
14. 在△ABC中，若AB＝3，BC＝5，则AC的取值范围是．

查看试题解析
15. 如图，在△ABC中，AD⊥BC于点D，BD＝DC，若BC＝6，AD＝7，则图中阴影部分图形的面积为．

查看试题解析
16. 如图，若△ABC≌△DEF，AF＝2，FD＝8，则FC的长度是．

查看试题解析
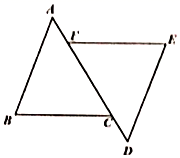17. 一个多边形的内角和是它的外角和的3倍，则这个多边形是边形．

查看试题解析
18. 《孙子算经》中记载了一道题，大意是：100匹马恰好拉了100片瓦，已知1匹大马能拉3片瓦，3匹小马能拉1片瓦，问有多少匹大马、多少匹小马？设有x匹大马，y匹小马，根据题意可列方程组为．

查看试题解析

三、解答题

19. 解方程：4x+3＝2（x﹣1）+1．

查看试题解析
20. 解方程组 ${\begin{array}{l} 3 x - 2 y = 6 \\ 2 x + 3 y = 17 \end{array}$

查看试题解析
21. 解不等式组： ${\begin{matrix} 3 x - 11 < x - 5 \\ 4 (x + 1) \leq 7 x + 10 \end{matrix}$ ，并把解集在数轴上表示出来．

查看试题解析
22. 已知关于x，y的方程组 ${\begin{array}{l} x - y = a + 3 \\ 2 x + y = 5 a \end{array}$ 的解满足x＜y，试求a的取值范围.

查看试题解析
23. 从甲地到乙地，长途汽车原来需要8小时，开通高速公路后，路程缩短了40千米．平均车速增加了30千米/时，需要4.5小时即可达到．求长途汽车原来行驶的速度．

查看试题解析
24. 如图，在直角△ABC中，CD是斜边AB上的高，∠BCD＝35°．

求：⑴∠EBC的度数；

⑵∠A的度数．对于上述问题，在以下解答过程的空白处填上适当的内容（理由或数学式）．

解：⑴∵CD⊥AB（已知），

∴∠CDB＝ ▲ ．

∵∠EBC＝∠CDB+∠BCD（）．

∴∠EBC＝ ▲ +35°＝ ▲ （等量代换）．

⑵∵∠EBC＝∠A+∠ACB（），

∴∠A＝∠EBC﹣∠ACB（等式的性质）．

∵∠ACB＝90°（已知），

∴∠A＝ ▲ ﹣90°＝ ▲ （等量代换）．

查看试题解析
25. 图①、图②、图③均是6×6的正方形网格，每个小正方形的顶点称为格点，小正方形的边长为1，点A、B、C均在格点上．只用无刻度的直尺，在给定的网格中按要求画图．

(1)、在图①中，将△ABC沿射线AC向下平移2个单位长度，画出平移后的三角形．

(2)、在图②中，画出以BC所在直线为对称轴且与△ABC成轴对称的三角形．

(3)、在图③中，将△ABC绕点C顺时针旋转90°，画出旋转后的三角形．

查看试题解析
26. 疫情期间为了满足口罩需求，某药店计划购买同一品牌的甲型口罩和乙型口罩．已知购买1个甲型口罩和2个乙型口罩需花费12元；购买10个甲型口罩和4个乙型口罩需花费40元．

(1)、购买该品牌一个甲型口罩、一个乙型口罩各需花费多少元？

(2)、如果药店需要甲型口罩的个数是乙型口罩个数的2倍还多8个，且该药店购买甲型口罩和乙型口罩的总费用不超过8000元，那么该药店最多可购买多少个该品牌乙型口罩？

查看试题解析

27. 教材呈现：如图是华师版七年级下册数学教材第76页的部分内容．

如图，已知△ABC分别用∠1、∠2、∠3表示△ABC的三个内角，证明∠1+∠2+∠3＝180°．

解：延长BC至点E，以点C为顶点，在BE的上侧作∠DCE＝∠2，则CD∥BA（同位角相等，两直线平行）

(1)、请根据教材提示，结合图一，将证明过程补充完整．

(2)、结论应用：

①如图二，在△ABC中，∠A＝60°，BP平分∠ABC，CP平分∠ACB，求∠BPC的度数．

②如图三，将△ABC的∠A折叠，使点A落在△ABC外的A₁处，折痕为DE．若∠A＝α，∠BDA₁＝β，∠CEA₁＝γ，则α、β、γ满足的等量关系为 ▲ （用含α、β、γ的代数式表示）．

查看试题解析

28. 如图，在长方形ABCD中，AB＝4，AD＝2．P是BC的中点，点Q从点A出发，以每秒1个单位长度的速度沿A→D→C→B→A的方向终点A运动，设点Q运动的时间为x秒．

(1)、点Q在运动的路线上和点C之间的距离为1时，x＝秒．

(2)、若△DPQ的面积为S，用含x的代数式表示S（0≤x＜7）．

(3)、若点Q从A出发3秒后，点M以每秒3个单位长度的速度沿A→B→C→D的方向运动，M点运动到达D点后立即沿着原路原速返回到A点．当M与Q在运动的路线上相距不超过2时，请直接写出相应x的取值范围．

查看试题解析