吉林省长春市二道区2020-2021学年七年级下学期数学期末试卷

试卷更新日期：2021-09-01 类型：期末考试

进入出卷网下载

一、单选题

1. 若 $4 x - 9 = x$ ，则 $x$ 的值是(　　　)

A、1 B、2 C、3 D、4

查看试题解析
2. 垃圾分类可以有效减少垃圾对环境的污染和节约资源，因此对生活垃圾分类提出更高要求，下面的垃圾分类标志是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 把不等式 $x + 1 \leq 3$ 的解集在数轴上表示出来，则正确的是（）

A、 B、 C、 D、

查看试题解析
4. 下列各组不是二元一次方程 $3 x + y = 5$ 的解的是

A、 ${\begin{array}{l} x = 0 \\ y = 5 \end{array}$ B、 ${\begin{array}{l} x = 1 \\ y = 2 \end{array}$ C、 ${\begin{array}{l} x = 2 \\ y = - 1 \end{array}$ D、 ${\begin{array}{l} x = - 1 \\ y = 2 \end{array}$

查看试题解析
5. 三角形的两边长分别为 $3 c m$ 和 $6 c m$ ，则第三边长可能为（）

A、 $2 c m$ B、 $3 c m$ C、 $6 c m$ D、 $9 c m$

查看试题解析
6. 如图，一扇窗户打开后，用窗钩AB可将其固定，这里所运用的几何原理是（）

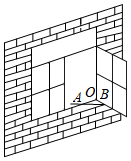A、两点确定一条直线 B、两点之间线段最短 C、三角形的稳定性 D、垂线段最短

查看试题解析
7. 如图，在△ABC中，∠ACB＝90°，将△ABC沿CD折叠，点B落在AC边上的点B′处，∠ADB′＝20°，则∠A的度数为（）

A、20° B、25° C、35° D、40°

查看试题解析
8. 如图，∠A+∠B+∠C+∠D+∠E+∠F的度数是（）

A、360° B、480° C、540° D、720°

查看试题解析

二、填空题

9. 若（a+3）x＞a+3的解集为x＜1，则a的取值范围是．

查看试题解析
10. 如果一个正多边形的每个内角都是150°，那么这个多边形的内角和为．

查看试题解析
11. 已知x、y满足方程组 ${\begin{matrix} x + 3 y = - 1 \\ 2 x + y = 3 \end{matrix}$ ，则 $x + y$ 的值为.

查看试题解析
12. 如图，AB $//$ CD，∠C＝27°，∠A＝60°，则∠E的大小为度．

查看试题解析
13. 如图所示，AD是△ABC的中线，点E是AD的中点，连接BE、CE，若△ABC的面积为8，则阴影部分的面积为.

查看试题解析
14. 如图，直角三角形ABC，AC＝3，BC＝4，AB＝5，点C、A在直线l上，将△ABC绕着点A顺时针转到位置①，得到点P₁ ，点P₁在直线l上，将位置①的三角形绕点P₁顺时针旋转到位置②，得到点P₂ ，点P₂在直线l上，……，按照此规律继续旋转，直到得到点P₂₀₂₁ ，则AP₂₀₂₁＝．

查看试题解析

三、解答题

15. 如图，△ABC≌△ADE，∠B＝10°，∠AED＝20°，AB＝4cm，点C为AD中点．

(1)、求∠BAE的度数和AE的长．

(2)、延长BC交ED于点F，则∠DFC的大小为度．

查看试题解析
16.

(1)、解方程：﹣（x﹣3）＝﹣2x﹣5．

(2)、解方程组： ${\begin{matrix} x - y = 1 \\ 3 x + y = 7 \end{matrix}$ ．

查看试题解析
17. 解不等式：2（x﹣5）＞﹣4，并把解集在下面的数轴上表示出来．

查看试题解析
18. 如图，BD为△ABC的角平分线，若∠ABC＝60°，∠ADB＝70°，点E为线段BC上一点，当△DCE为直角三角形时，求∠BDE的度数．

查看试题解析
19. 甲、乙两地相距3千米，小王从甲地出发步行到乙地，小李从乙地出发步行到甲地．两人同时出发，20分钟后两人相遇．已知小王的速度比小李的速度每小时快1千米，求两人的速度．

查看试题解析
20. 在直角三角形ABC中，∠ACB＝90°，AC＝4cm，BC＝3cm，△ABC沿AB方向平移至△DEF，若AE＝8cm，DB＝2cm．

(1)、AC和DF的关系为．

(2)、∠BGF＝°．

(3)、求△ABC沿AB方向平移的距离．

(4)、四边形AEFC的周长＝cm．

查看试题解析
21. 如图，在正方形网格中，△ABC的三个顶点都在格点上，点O在格点上．

(1)、画△A′B′C′，使△A'B'C′与△ABC关于直线OP成轴对称．

(2)、画△A′′B′′C′′，使△A′′B′′C′′与△A′B′C′关于点O成中心对称．

查看试题解析

22. 某电子超市销售甲、乙两种型号的蓝牙音箱，每台进价分别为240元、140元，如表是近两周的销量情况：

销售时段	销售数量		销售收入
销售时段	甲种型号	乙种型号	销售收入
第一周	3台	7台	2160元
第二周	5台	14台	4020元

(1)、求甲、乙两种型号蓝牙音箱的销售单价．

(2)、若超市准备用不多于6000元的资金再采购这两种型号的蓝牙音箱共30台，则甲种型号的蓝牙音箱最多能采购多少台？

查看试题解析

23. 三个数a，b，c，用M{a，b，c}表示这三数的平均数，用max{a，b，c}表示这三个数中最大的数．例如：M{﹣1，2，3} $= \frac{- 1 + 2 + 3}{3} = \frac{4}{3}$ ，max{﹣1，2，3}＝3．max{﹣1，5，a} $= {\begin{matrix} a (a \geq 5) \\ 5 (a < 5) \end{matrix}$ ，请解决以下问题：

(1)、填空：M{﹣（﹣2），﹣|﹣3|，（﹣3）²}＝．

(2)、当max{x，5，4+2x}＝5时，求x的取值范围．

(3)、当M{a，b，c}＝max{a，b，c}时，那么a、b、c之间存在一定的数量关系，请同学们补全下列的证明过程，并写出最后的结论．
证明：由M{a，b，c}＝max{a，b，c}，设max{a，b，c}＝a

∵M{a，b，c}＝（用含有a、b、c的代数式表示）

∴b+c＝， ①

又∵ ${\begin{matrix} a \geq b \\ a \geq c \end{matrix}$ ，即 ${\begin{matrix} \frac{a + b + c}{3} \geq b \\ \frac{a + b + c}{3} \geq c \end{matrix}$ ，

整理得 ${\begin{matrix} a + c \geq 2 b ② \\ a + b \geq 2 c ③ \end{matrix}$ ．

由①②可得：cb，（用不等号连接）

由①③可得：cb，（用不等号连接）

∴c＝b．

将c＝b代入①，得ac，（用等号或不等号连接）

所以可得a、b、c的数量关系为．

查看试题解析
24. 如图①，点O为数轴原点，OA＝3，正方形ABCD的边长为6，点P从点O出发，沿射线OA方向运动，速度为每秒2个单位长度，设运动时间为t秒，回答下列问题．

(1)、点A表示的数为，点D表示的数为．

(2)、t秒后点P对应的数为（用含t的式子表示）．

(3)、当PD＝2时，求t的值．

(4)、如图②，在点P运动过程中，作线段PE＝3，点E在点P右侧，以PE为边向上作正方形PEFG，当正方形PEFG与正方形ABCD重叠面积为6时，直接写出t的值．

查看试题解析