黑龙江省哈尔滨市通河县2020-2021学年七年级下学期数学期末试卷
试卷更新日期:2021-09-01 类型:期末考试
一、单选题
-
1. 在实数 , , , , ,0中,无理数的个数为( )A、1个 B、2个 C、3个 D、4个2. 如图是一个不等式组的解集在数轴上的表示,则该不等式组的解集是( )
 A、 B、 C、 D、3. 下列调查,适合全面调查的是( )A、调查某批次汽车的抗撞能力 B、调查春节联欢晚会的收视率 C、鞋厂检测生产的鞋底能承受的弯折次数 D、了解某班学生的身高情况4. 下列各点中,在第二象限的是( )A、(﹣1,3) B、(1,﹣3) C、(﹣1,﹣3 ) D、(1,3)5. 如图,若 ,则可推出 ,其推理的根据是( )
A、 B、 C、 D、3. 下列调查,适合全面调查的是( )A、调查某批次汽车的抗撞能力 B、调查春节联欢晚会的收视率 C、鞋厂检测生产的鞋底能承受的弯折次数 D、了解某班学生的身高情况4. 下列各点中,在第二象限的是( )A、(﹣1,3) B、(1,﹣3) C、(﹣1,﹣3 ) D、(1,3)5. 如图,若 ,则可推出 ,其推理的根据是( ) A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、内错角相等,两直线平行6. 下列式子正确的是( )A、 B、 C、 D、7. 若 ,则下列式子正确的是( )A、 B、 C、 D、8. 张翔从学校出发骑自行车去县城,中途因道路施工步行了一段路, 后到达县城.他骑车的平均速度是 ,步行的平均速度是 ,路程全长 .他骑车与步行各走了多少千米?设他骑自行车行了 ,步行走了 ,则可列方程组为( )A、 B、 C、 D、9. 如图,已知点 为 内一点, , , 交 于点 ,若 ,则 的度数为( )
A、两直线平行,同位角相等 B、同位角相等,两直线平行 C、两直线平行,内错角相等 D、内错角相等,两直线平行6. 下列式子正确的是( )A、 B、 C、 D、7. 若 ,则下列式子正确的是( )A、 B、 C、 D、8. 张翔从学校出发骑自行车去县城,中途因道路施工步行了一段路, 后到达县城.他骑车的平均速度是 ,步行的平均速度是 ,路程全长 .他骑车与步行各走了多少千米?设他骑自行车行了 ,步行走了 ,则可列方程组为( )A、 B、 C、 D、9. 如图,已知点 为 内一点, , , 交 于点 ,若 ,则 的度数为( ) A、 B、 C、 D、10. 若关于 的不等式组 无解,则 的取值范围是( )A、 B、 C、 D、
A、 B、 C、 D、10. 若关于 的不等式组 无解,则 的取值范围是( )A、 B、 C、 D、二、填空题
-
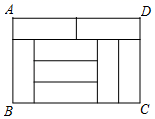
11. 的平方根是12. 已知 是方程 的一个解,则 的值为.13. 的小数部分为.14. 在画频数分布直方图时,一个样本容量为 的样本,最小值为 ,最大值为 .若确定组距为 ,则分成的组数是.15. 如图,由 个大小相同的小长方形无缝拼接成一个大长方形,已知大长方形的周长为 ,则小长方形的周长为 .
 16. 二元一次方程 中,若 的取值范围是 ,则 的最大值是.17. 点M(-3,-5)关于x轴的对称点的坐标是 .18. 关于x、y的二元一次方程组 的解满足x+y>2,则a的取值范围为 .19. 已知点 , 轴,且 ,则 点的坐标为 .20. 如图,已知 , 、 为 上的两点, 、 为 上的两点,延长 于点 , 平分 ,点 在直线 上,且 平分 ,若 .则下列结论:① ;② ;③ ;④设 , ;⑤ 的度数为50°.其中正确结论为 . (填序号)
16. 二元一次方程 中,若 的取值范围是 ,则 的最大值是.17. 点M(-3,-5)关于x轴的对称点的坐标是 .18. 关于x、y的二元一次方程组 的解满足x+y>2,则a的取值范围为 .19. 已知点 , 轴,且 ,则 点的坐标为 .20. 如图,已知 , 、 为 上的两点, 、 为 上的两点,延长 于点 , 平分 ,点 在直线 上,且 平分 ,若 .则下列结论:① ;② ;③ ;④设 , ;⑤ 的度数为50°.其中正确结论为 . (填序号)
三、解答题
-
21.(1)、解方程组: ;(2)、解不等式 ,并把解集在数轴上表示出来,并写出它的最大整数解.22. 如图,三角形 在平面直角坐标系中第二象限内,顶点 的坐标是 ,先把三角形 向右平移4个单位,再向下平移3个单位得到三角形 .
 (1)、请在图中作出三角形 ;(2)、点 的坐标为;点 的坐标为;点 的坐标为;(3)、求三角形 的面积.23. 某校为了进一步丰富学生的课外阅读,准备购买一批课外书,为此对学校部分学生进行了“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
(1)、请在图中作出三角形 ;(2)、点 的坐标为;点 的坐标为;点 的坐标为;(3)、求三角形 的面积.23. 某校为了进一步丰富学生的课外阅读,准备购买一批课外书,为此对学校部分学生进行了“你最喜欢的书籍”问卷调查(每人只选一项).根据收集到的数据,绘制成如下统计图(不完整):
请根据图中提供的信息,完成下列问题:
(1)、在这次问卷调查中,一共调查了名学生,并将上面的条形统计图补充完整;(2)、扇形统计图中 , “体育”所对的圆心角的度数为度;(3)、如果全校共有学生 人,请通过计算估计该校最喜欢“文学”类的学生比最喜欢“天文”类的学生多多少人.24. 已知,如图,在三角形 中, 平分 交 于点 , , 分别在 , 的延长线上, , . (1)、求证: ;(2)、若 , 比 大 ,求 的度数25. 某班计划购买篮球和排球若干个,买4个篮球和3个排球需要410元;买2个篮球和5个排球需要310元.(1)、篮球和排球单价各是多少元?(2)、若两种球共买30个,费用不超过1700元,篮球最多可以买多少个?(3)、如果购买这两种球刚好用去520元,问有哪几种购买方案?26. 如图,在长方形 中, 为平面直角坐标系的原点,点 的坐标为 ,点 的坐标为 ,且 , 满足 ,点 在第一象限内,点 从原点出发,以每秒2个单位长度的速度沿着 的线路移动.
(1)、求证: ;(2)、若 , 比 大 ,求 的度数25. 某班计划购买篮球和排球若干个,买4个篮球和3个排球需要410元;买2个篮球和5个排球需要310元.(1)、篮球和排球单价各是多少元?(2)、若两种球共买30个,费用不超过1700元,篮球最多可以买多少个?(3)、如果购买这两种球刚好用去520元,问有哪几种购买方案?26. 如图,在长方形 中, 为平面直角坐标系的原点,点 的坐标为 ,点 的坐标为 ,且 , 满足 ,点 在第一象限内,点 从原点出发,以每秒2个单位长度的速度沿着 的线路移动. (1)、 , , 点 的坐标为;(2)、当点 移动4秒时,求点 的坐标;(3)、在移动过程中,当点 到 轴的距离为5个单位长度时,求点 移动的时间.27. 已知 .
(1)、 , , 点 的坐标为;(2)、当点 移动4秒时,求点 的坐标;(3)、在移动过程中,当点 到 轴的距离为5个单位长度时,求点 移动的时间.27. 已知 .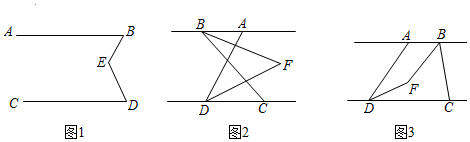 (1)、如图1, 为 , 之间一点,连接 , ,得到 .求证: ;(2)、如图,连接 , , 平分 , 平分 ,且 , 所在的直线交于点 .
(1)、如图1, 为 , 之间一点,连接 , ,得到 .求证: ;(2)、如图,连接 , , 平分 , 平分 ,且 , 所在的直线交于点 .①如图2,当点 在点 的左侧时,若 , ,求 的度数.
②如图3,当点 在点 的右侧时,设 , ,请你求出 的度数.(用含有 , 的式子表示)